Оценка значимости множественного уравнения регрессии в целом проводится с помощью 
, (критерия Фишера).
(9.163)
где:
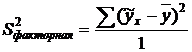– факторная дисперсия (9.164)
– остаточная дисперсия (9.165)
F-критерий можно рассчитать и по формуле:
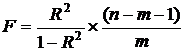(9.166)
где:
- для линейной множественной модели – число факторов включенных в регрессионную модель. Для нелинейной модели - число параметров при 
и их линеаризации (
и так далее), которое может быть больше числа факторов
- число наблюдений
Если расчетный 
превышает табличный при определенном уровне значимости 
или 
, и числе свободы - 
, 
(таблицы Снедекора-Фишера – приложение 2) можно сказать, что уравнение множественной регрессии статистически значимо.
Величина позволяет также оценить статистическую значимость и коэффициента (индекса) множественной корреляции 
.
Кроме оценки уравнения в целом, большое практическое значение имеет статистическая оценка значимости каждого отдельно включенного в модель фактора, через частные критерии Фишера 
, (
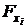). Данная оценка позволяет оценить целесообразность включения в модель множественной регрессии каждого из факторов после введения в модель остальных факторов.
Расчет частного , для фактора 
проводится по формуле:
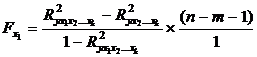(9.167)
- коэффициент множественной детерминации для модели, включающей все факторы
- коэффициент множественной детерминации для модели, без включения фактора 
Расчета частного в общем виде, для фактора 
проводится по формуле:
(9.168)
Расчета частного , для оценки значимости влияния фактора 
после включения в модель других факторов проводится по формуле:
(9.169)
Если величина расчетного частного 
превышает величину табличного при определенном уровне значимости или 
, и числе свободы - 
, 
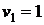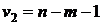(таблицы Снедекора-Фишера – приложение 2), можно сказать, что включение в модель фактора 
, после введения в модель остальных факторов, целесообразно. Если величина расчетного частного меньше табличного значения, можно сказать, что включение в модель фактора , после введения в модель остальных факторов, статистически неоправданно, и его необходимо исключить из рассматриваемой модели.
Зная величину частного критерия Фишера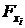 
, рассчитывают частные критерии Стьюдента, для определения значимости каждого из коэффициентов чистой регрессии 
.
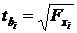(9.170)
Критерий Стьюдента 
также можно рассчитать по формуле:
(9.171)
где:
- коэффициент чистой регрессии для фактора 
- стандартная ошибка 
(9.172)
где:
- коэффициент детерминации множественного уравнения регрессии
- коэффициент множественной детерминации зависимости фактора со всеми остальными факторами уравнения множественной регрессии
- среднеквадратическое отклонение результативного признака
- среднеквадратическое отклонение факторного признака
Полученные фактические значения критерия Стьюдента сравнивают с табличными значениями при определенном уровне значимости 
, 
или 
, и числе степеней свободы 
(приложение 1). Если фактическое значение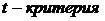 
больше табличного соответствующий коэффициент регрессии статистически значим.
Фактические значения критерия Стьюдента сравнивают с табличными значениями при определенном уровне значимости , или , и числе степеней свободы 
, где 
- число исключенных переменных (приложение 1). Если фактическое значение 
больше табличного соответствующий коэффициент частной корреляции статистически значим.
Пример 9.22. По данным примеров 9.20 и 9.21 необходимо:
1. провести оценку существенности уравнения регрессии и его параметров:
2. рассчитать частные 
. Оценить с их помощью статистическую значимость включения факторов , 
, 
, решить вопрос включения в регрессионную модель одних факторов после включения других.
Решение.
1. Оценку существенности множественного уравнения проведем, используя критерий Фишера (F-критерий)
.
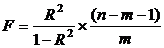где:
– число факторов включенных в регрессионную модель.
– число наблюдений
Табличное значение для данной модели при уровне значимости 
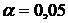, и числе свободы – 
, 
(значение 35 в приложении 2 отсутствует, возьмем ближайшее значение 30) будет равно 2,69.
Расчетное значение значительно больше табличного, соответственно множественное уравнение регрессии признается статистически значимым.
Расчет фактического , в программе Microsoft Excel – рисунок 9.
2. Рассчитаем частные для оценки значимости влияния фактора после включения в модель других факторов
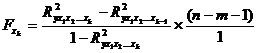
Табличное значение при уровне значимости , и числе свободы - 
, 
будет равно 4,12.
а) 
Фактическое значение больше табличного. Значит включение в модель фактора после факторов 
, 
, 
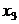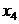статистически значимо.
б) 
Фактическое значение больше табличного. Значит включение в модель фактора после факторов , , 
статистически значимо.
в) 
Фактическое значение больше табличного. Значит включение в модель фактора после факторов , , статистически значимо.
г) 
Фактическое значение больше табличного. Значит включение в модель фактора 
после факторов , , статистически значимо.
где: 
– коэффициент множественной детерминации для множественной регрессионной модели со всеми включенными в нее факторами.
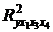– коэффициент множественной детерминации для множественной регрессионной модели без фактора .
– коэффициент множественной детерминации для множественной регрессионной модели без фактора 
.
– коэффициент множественной детерминации для множественной регрессионной модели без фактора 
.
– коэффициент множественной детерминации для множественной регрессионной модели без фактора 
.
Значения коэффициентов 
, 
, 
, 
, 
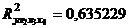рассчитаем в программе Microsoft Excel, методика расчета рассмотрена в примере 20 рисунок 9.
3. Статистическую оценку значимости коэффициентов регрессии 
по 
Стьюдента. Зная частные воспользуемся следующей формулой:
а) 
б) 
в) 
г) 
Табличное значение критерия Стьюдента при 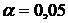, и числе степеней свободы 
(значение 35 в приложении 1 отсутствует, возьмем ближайшее значение 30) равно 2,0423. Все фактические значения критерия Стьюдента больше табличного, то есть можно сделать вывод о статистической значимости всех коэффициентов регрессии .
Расчет 
и критериев Стьюдента для в программе Microsoft Excel приведен на рисунке 9. обозначен как F, а критерии Стьюдента как t-статистика.
Контрольные вопросы
