Естественно, что кроме линейных взаимосвязей между явлениями природы, и тем более общественного мира существуют связи нелинейные. Соответственно изучать нелинейные связи при помощи линейной регрессии было бы не верно, для этого необходимо использовать нелинейные регрессии.
Но использование нелинейных регрессий связанно следующим ограничением – так как, параметры уравнения регрессии находят при помощи МНК, решая систему нормальных уравнений, а этот метод позволяет оценивать параметры или линейных уравнений или уравнений приводимых к линейному виду, то выбор нелинейных регрессий ограничен – должна существовать возможность линеаризации данных функций.
Регрессии, приводимые к линейному виду, подразделяют на два класса:
I. нелинейные относительно включенного в модель фактора (независимой переменной), но линейны относительно результата (зависимой переменной).
К первому классу относятся такие функции как, например:
· полиномы разных степеней;
· 
- полином второй степени
· 
- полином третьей степени и т.д.
· равносторонняя гипербола: 
.
II. нелинейные относительно включенного в модель результата, но линейны относительно фактора.
Ко второму классу относятся такие функции как, например:
· степенная функция: 
.
· показательная: 
.
· экспоненциальная: 
.
Рассмотрим линеаризацию наиболее часто применяемых функций:
Линеаризация полиномов разных степеней
Проводится следующим образом.
В параболе второй степени,
(9.52)
заменяя переменные 
, получим двухфакторное линейное уравнение регрессии:
(9.53)
В параболе третьей степени,
(9.54)
заменяя переменные 
, получим трехфакторное линейное уравнение регрессии:
(9.55)
Аналогичным образом поступим с полиномами более высоких порядков.
Из полиномов наибольшее распространение получила парабола второго порядка.
МНК для оценки параметров функция регрессии по линеаризованной параболе второго порядка дает следующую систему уравнений:
(9.56)
Пример 9.11. Имеются данные о средней прибыли 
(млн. руб.) и затратах на рекламу 
(млн. руб.) за декаду, по выборке, равной 15-ти предприятиям сферы торговли. Рассчитать функцию регрессии параболы второго порядка 
Таблица 9.22
| № | 
| 
|
| 1 | 37,8 | 0,3 |
| 2 | 38,0 | 0,5 |
| 3 | 39,0 | 0,7 |
| 4 | 37,5 | 0,8 |
| 5 | 39,5 | 0,9 |
| 6 | 36,8 | 1,1 |
| 7 | 40,0 | 1,3 |
| 8 | 40,1 | 1,6 |
| 9 | 40,0 | 1,7 |
| 10 | 39,0 | 2,2 |
| 11 | 38,0 | 2,5 |
| 12 | 41,0 | 2,6 |
| 13 | 41,6 | 2,7 |
| 14 | 41,0 | 3,0 |
| 15 | 41,9 | 3,2 |
Решение. МНК для расчета параметров параболы второго порядка дает систему уравнений:
В таблице 9.23 рассчитаем все возможные значения.
Таблица 9.23
| № |
|
| 
| 
| 
| 
| 
| 
|
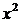
| 1 | 37,80 | 0,30 | 0,09 | 0,027 | 0,0081 | 11,34 | 3,402 | 38,023560 |
| 2 | 38,00 | 0,50 | 0,25 | 0,125 | 0,0625 | 19,00 | 9,500 | 38,158005 |
| 3 | 39,00 | 0,70 | 0,49 | 0,343 | 0,2401 | 27,30 | 19,110 | 38,307508 |
| 4 | 37,50 | 0,80 | 0,64 | 0,512 | 0,4096 | 30,00 | 24,000 | 38,387907 |
| 5 | 39,50 | 0,90 | 0,81 | 0,729 | 0,6561 | 35,55 | 31,995 | 38,472071 |
| 6 | 36,80 | 1,10 | 1,21 | 1,331 | 1,4641 | 40,48 | 44,528 | 38,651694 |
| 7 | 40,00 | 1,30 | 1,69 | 2,197 | 2,8561 | 52,00 | 67,600 | 38,846375 |
| 8 | 40,10 | 1,60 | 2,56 | 4,096 | 6,5536 | 64,16 | 102,656 | 39,166634 |
| 9 | 40,00 | 1,70 | 2,89 | 4,913 | 8,3521 | 68,00 | 115,600 | 39,280917 |
| 10 | 39,00 | 2,20 | 4,84 | 10,648 | 23,4256 | 85,80 | 188,760 | 39,908803 |
| 11 | 38,00 | 2,50 | 6,25 | 15,625 | 39,0625 | 95,00 | 237,500 | 40,330713 |
| 12 | 41,00 | 2,60 | 6,76 | 17,576 | 45,6976 | 106,60 | 277,160 | 40,478879 |
| 13 | 41,60 | 2,70 | 7,29 | 19,683 | 53,1441 | 112,32 | 303,264 | 40,630810 |
| 14 | 41,00 | 3,00 | 9,00 | 27,000 | 81,0000 | 123,00 | 369,000 | 41,109192 |
| 15 | 41,90 | 3,20 | 10,24 | 32,768 | 104,8576 | 134,08 | 429,056 | 41,446938 |
| Итого | 591,20 | 25,10 | 55,01 | 137,573 | 367,7897 | 1004,63 | 2223,131 | 591,200005 |
Подставим эти значения в систему уравнений.
Разделим каждое из уравнений системы на число при 
, первое на 15, второе на 25,01 и третье на 55,01.
Далее вычтем из 5-го уравнения 4-е, и из 6-го уравнения 5-е. система примет вид:
Разделим каждое уравнение на число при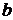 
, 7-е на 0,5183, а 8-е на 0,30924
Вычтем из 10-го уравнения 9-е
Значение параметра 
Подставим значение параметра 
в уравнение (9) и найдем значение параметра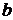
Подставим значение параметров 
в уравнение (1) и найдем значение параметра
Подставим параметры в уравнение
Подставляя в полученное уравнение и 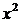рассчитаем теоретические значения 
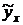, занесем их в последний столбик таблицы.
Линеаризация равносторонней гиперболы
(9.57)
проводят, заменяя 
на 
, в результате получим уравнение линейной регрессии:
(9.58)
МНК для оценки параметров функция регрессии по линеаризованной равносторонней гиперболе дает следующую систему уравнений:
(9.59)
Также можно использовать уравнения:
(9.60)
(9.61)
Пример 9.12. Имеются данные о средней прибыли (млн. руб.) и затратах на рекламу (млн. руб.) за декаду, по выборке, равной 15-ти предприятиям сферы торговли. Рассчитать функцию регрессии равносторонней гиперболы 
Таблица 9.24
| № |
|
|
| 1 | 37,8 | 0,3 |
| 2 | 38,0 | 0,5 |
| 3 | 39,0 | 0,7 |
| 4 | 37,5 | 0,8 |
| 5 | 39,5 | 0,9 |
| 6 | 36,8 | 1,1 |
| 7 | 40,0 | 1,3 |
| 8 | 40,1 | 1,6 |
| 9 | 40,0 | 1,7 |
| 10 | 39,0 | 2,2 |
| 11 | 38,0 | 2,5 |
| 12 | 41,0 | 2,6 |
| 13 | 41,6 | 2,7 |
| 14 | 41,0 | 3,0 |
| 15 | 41,9 | 3,2 |
МНК для оценки параметров функция регрессии по линеаризованной равносторонней гиперболе дает следующую систему уравнений:
В таблице 9.25 рассчитаем все возможные значения:
Таблица 9.25
| № |
|
| 
| 
| 
|
|
| 1 | 37,80 | 0,30 | 3,333333 | 126,000000 | 11,111111 | 36,808395 |
| 2 | 38,00 | 0,50 | 2,000000 | 76,000000 | 4,000000 | 38,266516 |
| 3 | 39,00 | 0,70 | 1,428571 | 55,714286 | 2,040816 | 38,891425 |
| 4 | 37,50 | 0,80 | 1,250000 | 46,875000 | 1,562500 | 39,086709 |
| 5 | 39,50 | 0,90 | 1,111111 | 43,888889 | 1,234568 | 39,238597 |
| 6 | 36,80 | 1,10 | 0,909091 | 33,454545 | 0,826446 | 39,459524 |
| 7 | 40,00 | 1,30 | 0,769231 | 30,769231 | 0,591716 | 39,612474 |
| 8 | 40,10 | 1,60 | 0,625000 | 25,062500 | 0,390625 | 39,770204 |
| 9 | 40,00 | 1,70 | 0,588235 | 23,529412 | 0,346021 | 39,810409 |
| 10 | 39,00 | 2,20 | 0,454545 | 17,727273 | 0,206612 | 39,956611 |
| 11 | 38,00 | 2,50 | 0,400000 | 15,200000 | 0,160000 | 40,016262 |
| 12 | 41,00 | 2,60 | 0,384615 | 15,769231 | 0,147929 | 40,033086 |
| 13 | 41,60 | 2,70 | 0,370370 | 15,407407 | 0,137174 | 40,048664 |
| 14 | 41,00 | 3,00 | 0,333333 | 13,666667 | 0,111111 | 40,089168 |
| 15 | 41,90 | 3,20 | 0,312500 | 13,093750 | 0,097656 | 40,111951 |
| Итого | 591,20 | 25,10 | 14,269937 | 552,158190 | 22,964285 | 591,199995 |
Подставим полученные значения в систему уравнений
Разделим первое уравнение на 15, а второе на 14,269937
Вычтем из второго уравнения первое
Подставим значение параметра 
в первое уравнение и рассчитаем параметр 
Уравнение регрессии примет вид
Подставляя в полученное уравнение регрессии значение 
, рассчитаем 
.
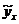Линеаризация степенной функции
(9.62)
проводят путем логарифмирования обеих частей уравнения, получая уравнение вида:
(9.63)
Обозначив через 
, получим линейное уравнение регрессии:
(9.64)
МНК для оценки параметров функция регрессии по линеаризованной степенной функции дает следующую систему уравнений:
(9.65)
Также можно использовать уравнения:
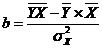(9.66)
(9.67)
Рассчитав параметры ,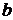 
и составив линейное уравнение регрессии необходимо провести его потенцирование, чтобы вернуться к степенной функции.
(9.68)
Пример 9.13. Имеются данные о средней прибыли (млн. руб.) и затратах на рекламу (млн. руб.) за декаду, по выборке, равной 15-ти предприятиям сферы торговли. Рассчитать степенную функцию 
Таблица 9.26
| № |
|
|
| 1 | 37,8 | 0,3 |
| 2 | 38,0 | 0,5 |
| 3 | 39,0 | 0,7 |
| 4 | 37,5 | 0,8 |
| 5 | 39,5 | 0,9 |
| 6 | 36,8 | 1,1 |
| 7 | 40,0 | 1,3 |
| 8 | 40,1 | 1,6 |
| 9 | 40,0 | 1,7 |
| 10 | 39,0 | 2,2 |
| 11 | 38,0 | 2,5 |
| 12 | 41,0 | 2,6 |
| 13 | 41,6 | 2,7 |
| 14 | 41,0 | 3,0 |
| 15 | 41,9 | 3,2 |
Решение. Для расчета параметров данной функции проведем ее линеаризацию, прологарифмировав обе части уравнения
Обозначив через , получим линейное уравнение регрессии:
МНК для оценки параметров функция регрессии по линеаризованной степенной функции дает следующую систему уравнений:
В таблице 9.27 рассчитаем все возможные значения:
Таблица 9.27
| № |
|
| 
| 
| 
|
|
| 1 | 37,80 | 0,30 | 1,577492 | -0,522879 | -0,824837 | 37,183851 |
| 2 | 38,00 | 0,50 | 1,579784 | -0,301030 | -0,475562 | 37,910774 |
| 3 | 39,00 | 0,70 | 1,591065 | -0,154902 | -0,246459 | 38,397333 |
| 4 | 37,50 | 0,80 | 1,574031 | -0,096910 | -0,152539 | 38,592153 |
| 5 | 39,50 | 0,90 | 1,596597 | -0,045757 | -0,073056 | 38,764817 |
| 6 | 36,80 | 1,10 | 1,565848 | 0,041393 | 0,064815 | 39,060772 |
| 7 | 40,00 | 1,30 | 1,602060 | 0,113943 | 0,182544 | 39,308870 |
| 8 | 40,10 | 1,60 | 1,603144 | 0,204120 | 0,327234 | 39,619441 |
| 9 | 40,00 | 1,70 | 1,602060 | 0,230449 | 0,369193 | 39,710581 |
| 10 | 39,00 | 2,20 | 1,591065 | 0,342423 | 0,544817 | 40,100534 |
| 11 | 38,00 | 2,50 | 1,579784 | 0,397940 | 0,628659 | 40,295293 |
| 12 | 41,00 | 2,60 | 1,612784 | 0,414973 | 0,669262 | 40,355237 |
| 13 | 41,60 | 2,70 | 1,619093 | 0,431364 | 0,698418 | 40,413002 |
| 14 | 41,00 | 3,00 | 1,612784 | 0,477121 | 0,769493 | 40,574705 |
| 15 | 41,90 | 3,20 | 1,622214 | 0,505150 | 0,819461 | 40,674075 |
| Итого | 591,20 | 25,10 | 23,929804 | 2,037398 | 3,301443 | 590,961438 |
| В среднем | 1,595320 | 0,135827 | 0,220096 | |||
| 0,089930 |
Подставим полученные значения в уравнение
Выполним потенцирование полученного уравнения
Подставляя в полученное уравнение значение фактора , рассчитаем .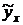
Линеаризация показательной функции
Показательная функция
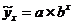(9.69)
также проводят путем логарифмирования обеих частей уравнения:
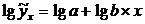(9.70)
Обозначив через 
, получим линейное уравнение регрессии:
(9.71)
МНК для оценки параметров функция регрессии по линеаризованной степенной функции дает следующую систему уравнений:
(9.72)
Также можно использовать уравнения:
(9.73)
(9.74)
Рассчитав параметры 
, и составив линейное уравнение регрессии необходимо провести его потенцирование, что бы вернуться к показательной функции.
(9.75)
Пример 9.14. Имеются данные о средней прибыли (млн. руб.) и затратах на рекламу (млн. руб.) за декаду, по выборке, равной 15-ти предприятиям сферы торговли. Рассчитать показательную функцию 
Таблица 9.28
| № |
|
|
| 1 | 37,8 | 0,3 |
| 2 | 38,0 | 0,5 |
| 3 | 39,0 | 0,7 |
| 4 | 37,5 | 0,8 |
| 5 | 39,5 | 0,9 |
| 6 | 36,8 | 1,1 |
| 7 | 40,0 | 1,3 |
| 8 | 40,1 | 1,6 |
| 9 | 40,0 | 1,7 |
| 10 | 39,0 | 2,2 |
| 11 | 38,0 | 2,5 |
| 12 | 41,0 | 2,6 |
| 13 | 41,6 | 2,7 |
| 14 | 41,0 | 3,0 |
| 15 | 41,9 | 3,2 |
Решение. Для расчета параметров данной функции проведем ее линеаризацию, прологарифмировав обе части уравнения
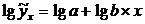
Обозначив через 
, получим линейное уравнение регрессии:
МНК для оценки параметров функция регрессии по линеаризованной степенной функции дает следующую систему уравнений:
В таблице 9.29 рассчитаем все возможные значения:
Таблица 9.29
| № |
|
|
| 
|
|
| 1 | 37,80 | 0,30 | 1,577492 | 0,473248 | 37,806262 |
| 2 | 38,00 | 0,50 | 1,579784 | 0,789892 | 38,032035 |
| 3 | 39,00 | 0,70 | 1,591065 | 1,113745 | 38,259157 |
| 4 | 37,50 | 0,80 | 1,574031 | 1,259225 | 38,373226 |
| 5 | 39,50 | 0,90 | 1,596597 | 1,436937 | 38,487635 |
| 6 | 36,80 | 1,10 | 1,565848 | 1,722433 | 38,717477 |
| 7 | 40,00 | 1,30 | 1,602060 | 2,082678 | 38,948692 |
| 8 | 40,10 | 1,60 | 1,603144 | 2,565031 | 39,298106 |
| 9 | 40,00 | 1,70 | 1,602060 | 2,723502 | 39,415272 |
| 10 | 39,00 | 2,20 | 1,591065 | 3,500342 | 40,006365 |
| 11 | 38,00 | 2,50 | 1,579784 | 3,949459 | 40,365268 |
| 12 | 41,00 | 2,60 | 1,612784 | 4,193238 | 40,485616 |
| 13 | 41,60 | 2,70 | 1,619093 | 4,371552 | 40,606323 |
| 14 | 41,00 | 3,00 | 1,612784 | 4,838352 | 40,970608 |
| 15 | 41,90 | 3,20 | 1,622214 | 5,191085 | 41,215278 |
| Итого | 591,20 | 25,10 | 23,929804 | 40,210718 | 590,987319 |
| В среднем | 1,673333 | 1,595320 | 2,680715 | ||
|
| 0,867289 |
Получили линеаризованное уравнение
Произведем потенцирование линейного уравнения для возврата к показательной функции.
Подставим в полученное уравнение значения фактора , рассчитаем значения .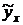
