Частные уравнения регрессии

Частные уравнения регрессии, рассчитываются на основе множественного уравнения регрессии:

                                                      (9.139)

Они показывают изолированное влияние одного конкретного  фактора на результативный признак , при зафиксированном, на среднем уровне, положении остальных, включенных в модель факторов. Влияния зафиксированных факторов в уравнениях частной регрессии присоединены к свободному члену уравнения регрессии .

Частные множественные регрессии записываются, как:

                                                                                              (9.140)

Обозначение  показывает, что изучается влияние на результат , фактора , при зафиксированном на среднем уровне положении факторов . Обозначение  показывает, что изучается влияние на результат , фактора , при зафиксированном на среднем уровне положении факторов , и т, д. Знак  в нижнем индексе обозначения отделяет фактор влияния, которого исследуется, от факторов, влияние которых изолируется.

Частные уравнения множественной регрессии для линейной модели имеют вид:

                                                     (9.141)

На основе частных уравнений регрессии рассчитывают частные коэффициенты эластичности:

                                                                                       (9.142)

Частные коэффициенты эластичности отличаются от средних коэффициентов.

Частный коэффициент эластичности показывает, на сколько, в среднем, процентов изменится результат при подстановке в уравнение регрессии конкретного значения .

Средний коэффициент эластичности показывает, на сколько в среднем процентов изменится результат, если соответствующий данному коэффициенту фактор увеличится на 1%, при зафиксированных, на средних уровнях величин остальных, включенных в модель, факторов.

                                                                                                              (9.143)

Пример 9.20. Имеются данные по 40 хозяйствам о средней урожайности (ц/га), качества почвы  (баллов), затратах труда  (чел-час./1га.), внесение минеральных удобрений  (ц.д.в. на 1га.), стоимость основных фондов  (тыс. руб. на 100 га.) (табл. 9.35).

Таблица 9.35

№	Урожайность, ц/га	Качество пашни, балов	Затраты труда чел.-час на 1 га	Внесение мин. удобрений на 1 га ц.д.в.	Стоимость ОФ на тыс.руб. 100 га
1	10,49	67	15,45	0,76	18,21	10,048113
2	8,57	53	16,13	1,06	19,17	9,601560
3	10,95	70	17,59	1,06	20,42	11,593826
4	9,23	51	18,84	0,52	20,00	8,633346
5	11,97	70	18,43	0,99	20,37	11,524121
6	8,56	56	12,44	0,67	21,04	8,887059
7	12,18	55	15,50	1,02	20,25	9,800000
8	7,93	47	16,34	0,44	17,68	7,427264
9	15,75	89	17,13	1,22	28,19	14,929855
10	13,61	74	17,10	0,72	22,63	11,502371
11	13,99	52	27,16	1,59	40,16	15,194027
12	12,57	87	14,92	1,23	21,12	13,414848
13	10,93	65	18,17	0,82	26,01	11,506605
14	9,86	54	17,24	0,98	17,99	9,461020
15	7,39	48	14,64	0,41	21,90	7,917362
16	9,23	61	14,70	0,79	20,47	9,804117
17	15,40	79	28,81	1,20	29,01	15,372985
18	13,14	85	21,87	0,99	23,40	13,824023
19	13,12	83	16,88	0,91	25,53	13,217642
20	10,27	64	16,65	0,83	21,18	10,512752
21	9,12	55	16,10	0,81	20,24	9,395289
22	13,42	72	18,02	1,21	20,22	12,140147
23	10,29	69	16,91	0,78	24,89	11,485126
24	11,55	72	14,90	0,86	20,86	11,101097
25	15,26	87	17,64	1,21	28,42	14,808601
26	12,35	79	14,41	1,20	19,73	12,305857
27	8,24	49	12,62	1,07	18,57	8,749497
28	10,41	64	18,13	0,79	21,07	10,573475
29	9,62	52	17,30	0,77	24,46	9,806811
30	10,76	65	17,16	0,82	20,46	10,532588
31	8,35	51	14,65	0,63	22,82	8,842748
32	10,31	75	13,66	0,79	19,89	10,941740
33	9,38	55	12,07	0,73	22,92	9,174913
34	14,93	72	14,38	1,05	33,99	13,502339
35	12,46	79	14,53	1,03	22,95	12,436891
36	10,45	59	16,54	0,92	23,20	10,534678
37	12,38	80	21,64	0,95	21,64	12,955222
38	7,74	76	10,27	0,65	16,87	9,872332
39	14,49	89	19,44	1,05	24,49	14,236792
40	8,50	47	15,05	0,56	17,89	7,582986
Итого	445,15	2657,00	671,41	36,09	900,31	445,152022
Среднее	11,128750	66,425000	16,785250	0,902250	22,507750
	2,305561	12,959335	3,458573	0,240692	4,463267

Необходимо построить уравнение множественной линейной регрессии, рассчитать парные коэффициенты регрессии, частные и средние коэффициенты эластичности, провести прогнозирование урожайности, при различных значениях факторов, то есть рассчитать:

· максимально возможную урожайность,

· минимальную урожайность,

· урожайность для средних значений фактора,

· частные уравнения регрессии, при максимальном значении одного фактора и средних значениях двух других факторов.

Решение.

1) Уравнение множественной линейной регрессии для данного примера имеет вид:

Для решения данного уравнения представим его в стандартизированном масштабе:

где: - стандартизованные переменные:

,

 - стандартизованные коэффициенты регрессии

МНК для решения множественного уравнения линейной регрессии в стандартизованном виде дает систему уравнений:

Для нашего примера:

Между стандартизированными переменными и коэффициентами парной корреляции существует следующая взаимосвязь: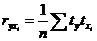

2) Рассчитаем коэффициенты парной корреляции. Расчет проведем, используя программу Microsoft, таблица 9.36.

Таблица 9.36

	Столбец 1 y	Столбец 2 x1	Столбец 3 x2	Столбец 4 x3	Столбец 5 x4
Столбец 1 y	1,000000
Столбец 2 x1	0,749996	1,000000
Столбец 3 x2	0,545459	0,188222	1,000000
Столбец 4 x3	0,731053	0,474013	0,466501	1,000000
Столбец 5 x4	0,640037	0,223318	0,549570	0,539163	1,000000

 

3) Подставим значения коэффициентов корреляции в систему.

Для решения системы уравнения воспользуемся методом Гаусса.

4). Составим матрицу, в которую внесем все числа (коэффициенты) при переменных , за горизонтальную черту вынесем итог по каждому уравнению:

 – матрица 1

5) Далее необходимо привести к нулю первые коэффициенты строк 2,3,4, первая строка остается без изменений – рабочая строка. Для этого:

а) Умножим первую (рабочую) строку на число противоположное 1-му коэффициенту второй строки матрицы 1, т.е. на , получим

суммируем полученную строку со второй строкой матрицы 1, получим расчетную строку 1.

б) Умножим первую (рабочую) строку на число противоположное 1-му коэффициенту третьей строки матрицы 1, т.е. на  получим

суммируем полученную строку с третьей строкой матрицы 1, получим расчетную строку 2.

в) Умножим первую (рабочую) строку на число противоположное 1-му коэффициенту четвертой строки матрицы 1, т.е. на  получим

суммируем полученную строку с четвертой строкой матрицы 1, получим расчетную строку 3.

6) Составим новую матрицу (матрица 2). Первой строкой данной матрицы будет первая строка матрицы 1, второй строкой (рабочей) – расчетная строка 1, третьей – строка 2, четвертой – строка 3.

 – матрица 2

7) Далее, необходимо привести к нулю вторые коэффициенты строк 3 и 4 матрицы 2, первая строка остается без изменений, рабочей будет вторая строка. Для этого:

а) Найдем число, которое при умножении на второй коэффициент рабочей строки матрицы 2 - , даст число, противоположное (с другим знаком) второму коэффициенту третьей строки - . Для этого найдем отношение: , так как второй коэффициент третьей строки число положительное, полученное число возьмем со знаком минус  и умножим на него вторую (рабочую) строку матрицы 2:

суммируем полученную строку с третьей строкой матрицы 2, получим расчетную строку 4:

б) Найдем число, которое при умножении на второй коэффициент рабочей строки матрицы 2 - , даст число, противоположное (с другим знаком) второму коэффициенту четвертой строки - . Для этого найдем отношение: , так как второй коэффициент четвертой строки число положительное, полученное число возьмем со знаком минус  и умножим на него вторую (рабочую) строку матрицы 2:

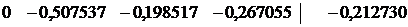
суммируем полученную строку с четвертой строкой матрицы 2, получим расчетную строку 5:

8). Составим новую матрицу – 3. Первые две строки возьмем без изменений из матрицы два, третьей строкой (рабочей) будет расчетная строка 4, четвертой строкой – расчетная строка 5.

 – матрица 3

9) Далее необходимо привести к нулю третий коэффициент строки 4. Для этого:

Найдем число, которое при умножении на третий коэффициент рабочей строки матрицы 3 - 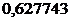, даст число, противоположное (с другим знаком) третьему коэффициенту четвертой строки - 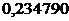. Для этого найдем отношение 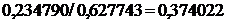, так как третий коэффициент четвертой строки число положительное, полученное число возьмем со знакам минус  и умножим на него третью (рабочую) строку матрицы 3.

суммируем полученную строку с четвертой строкой матрицы 3

10) Составим новую матрицу – 4. Первые три строки возьмем без изменений из матрицы три, а четвертой строкой – расчетная строка 6.

 – матрица 4

 

11) Подставим полученные коэффициенты в систему

12) Рассчитаем значение стандартизированных коэффициентов регрессии .

а) Из четвертого уравнения системы рассчитаем :

б) Подставим полученное значения  в третье уравнение системы и рассчитаем значение :

в) Подставим значения  и  во второе уравнения системы и получим значение :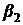

г) Подставим значения , ,  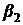во второе уравнения системы и получим значение :

13) Зная, что между b -коэффициентами и коэффициентами регрессии в натуральном масштабе  существует следующая взаимосвязь:

 соответственно

а)

 б)

в)

г)

Таким образом, используя метод Гаусса, рассчитали коэффициенты регрессии , параметр  найдем по формуле:

14) Подставим рассчитанные параметры в уравнение множественной регрессии:

а) Коэффициент регрессии  показывает, что при увеличении фактора  - качество пашни на 1 балл, средняя урожайность в среднем возрастет на 0,096083 ц/га., при фиксированном положении остальных факторов.

б) Коэффициент регрессии  показывает, что при увеличении фактора  - затраты труда на 1 чел.-час./га, средняя урожайность в среднем возрастет на 0,113165 ц/га., при фиксированном положении остальных факторов.

в) Коэффициент регрессии  показывает, что при увеличении фактора  - внесение минеральных удобрений на 1 ц.д.в./га средняя урожайность в среднем возрастет на 2,243155 ц/га., при фиксированном положении остальных факторов.

г) Коэффициент регрессии  показывает, что при увеличении фактора  - стоимость ОФ на одну тыс.руб./100га, средняя урожайность в среднем возрастет на 0,15490 ц/га., при фиксированном положении остальных факторов.

15) Проведем прогнозирование средней урожайности на основе полученного уравнения множественной регрессии:

а) Рассчитаем максимально возможную урожайность, для этого по каждому из факторов , в уравнение подставим максимальное значение, если коэффициент 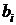 регрессии для данного фактора положителен, или минимальное значение, если коэффициент регрессии  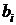для данного фактора отрицателен. В данном примере все коэффициенты регрессии  положительны, соответственно значения факторов берем максимальные , , , , 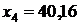и подставляем в уравнение.

б) Рассчитаем минимально возможную урожайность, для этого по каждому из факторов , в уравнение подставим минимальное значение, если коэффициент 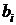 регрессии для данного фактора положителен, или максимальное значение, если коэффициент регрессии  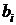для данного фактора отрицателен. В данном примере все коэффициенты регрессии  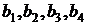положительны, соответственно значения факторов берем минимальные , , , , и подставляем в уравнение.

в) Рассчитаем среднюю возможную урожайность, для этого по каждому из факторов , в уравнение подставим средние значения , , , .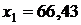

16) Рассчитаем частные уравнения регрессии

а) Рассчитаем среднюю возможную урожайность при максимальном значении фактора  (учитывая знак коэффициента регрессии), и зафиксированных на среднем уровне значении остальных факторов , , .

б) Рассчитаем среднюю возможную урожайность при максимальном значении фактора 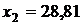 (учитывая знак коэффициента регрессии), и зафиксированных на среднем уровне значении остальных факторов , , .

в) Рассчитаем среднюю возможную урожайность при максимальном значении фактора  (учитывая знак коэффициента регрессии), и зафиксированных на среднем уровне значении остальных факторов , , .

г) Рассчитаем среднюю возможную урожайность при максимальном значении фактора 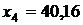 (учитывая знак коэффициента регрессии), и зафиксированных на среднем уровне значении остальных факторов , , .

17) На основе частных уравнений регрессии рассчитаем частные коэффициенты эластичности:

а) При максимальном значении фактора , и зафиксированных на среднем уровне значении остальных факторов , , .

то есть средняя урожайность в среднем возрастет, при подстановке в уравнение регрессии конкретного значения  на 0,64%, и зафиксированных на среднем уровне значении остальных факторов.

б) При максимальном значении фактора 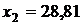 (учитывая знак коэффициента регрессии), и зафиксированных на среднем уровне значении остальных факторов , , .

то есть средняя урожайность в среднем возрастет, при подстановке в уравнение регрессии конкретного значения  на 0,26%, и зафиксированных на среднем уровне значении остальных факторов.

в) При максимальном значении фактора  (учитывая знак коэффициента регрессии), и зафиксированных на среднем уровне значении остальных факторов , , .

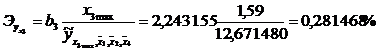
то есть средняя урожайность в среднем возрастет, при подстановке в уравнение регрессии конкретного значения  на 0,28%, и зафиксированных на среднем уровне значении остальных факторов.

г) При максимальном значении фактора 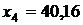 (учитывая знак коэффициента регрессии), и зафиксированных на среднем уровне значении остальных факторов , , .

то есть средняя урожайность в среднем возрастет, при подстановке в уравнение регрессии конкретного значения 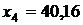 на 0,45%, и зафиксированных на среднем уровне значении остальных факторов.

18) Рассчитаем средние коэффициенты эластичности для каждого фактора:

а) Рассчитаем средний коэффициент эластичности для фактора

то есть средняя урожайность, при увеличении фактора на 1%, в среднем возрастет на 0,57%, при фиксированном положении остальных факторов.

б) Рассчитаем средний коэффициент эластичности для фактора

 

то есть средняя урожайность, при увеличении фактора на 1%, в среднем возрастет на 0,17%, при фиксированном положении остальных факторов.

в) Рассчитаем средний коэффициент эластичности для фактора

 

то есть средняя урожайность, при увеличении фактора на 1%, в среднем возрастет на 0,18%, при фиксированном положении остальных факторов.

г) Рассчитаем средний коэффициент эластичности для фактора

 

то есть средняя урожайность, при увеличении фактора на 1%, в среднем возрастет на 0,31%, при фиксированном положении остальных факторов.

19) Коэффициенты средней эластичности позволяют ранжировать факторы по степени их влияния на результативный признак, для нашего примера:

1.  - качество пашни, балов

2. - стоимость ОФ тыс.руб. на 100га

3. - внесение минеральных удобрений на 1га.тыс.руб.

4. - затраты труда, чел.-час.

20) Расчет множественной регрессионной модели в программе Microsoft Excel аналогичен расчету парной регрессии и рассмотрен в примере 1 (вводим входной интервал, выделяя все столбики содержащие факторы ). Для данного примера приведем таблицу, содержащую результаты – рисунок 9.9.

Рисунок 9.9

Параметр  в данной таблице находится на пересечении столбика «Коэффициенты» и строки «Y-пересечение», параметр - на пересечении столбика «Коэффициенты» и строки «Переменная Х1», - строки «Переменная Х2», - строки «переменная Х3», - строки «Переменная Х4».

Множественная корреляция

Силу связи во множественных моделях изучают с помощью показателя множественной корреляции и его квадрата – показателя множественной детерминации.

Показатель множественной корреляции  – показывает тесноту связи между результативным признаком и всеми включенными в модель факторами. Может принимать значения от 0 до 1, то есть в отличие от парной модели не показывает направление связи.

Показатель множественной детерминации  - показывает часть вариации результативного признака, которая сложилась под влиянием всех включенных в модель факторов.

В статистике и эконометрике показатель множественной корреляции (детерминации) принято называть индексом или коэффициентом множественной (совокупной) корреляции.

Для линейной множественной функции и для функций нелинейных по переменным (полиномы разных степеней, равносторонняя гипербола и т.п. функции) индекс множественной корреляции совпадает скоэффициентом множественной корреляции.

Коэффициент (индекс) множественной корреляции рассчитывают, используя следующие формулы:

                                                                                           (9.144)

где:

- остаточная дисперсия                                              (9.145)

 - общая дисперсия для признака                                              (9.146)

                                                                          (9.147)

Коэффициент множественной корреляции можно рассчитать и, как:

                     (9.148)

где:

- парные коэффициенты корреляции между результативным признаком и одним из факторов .

Для функций нелинейных по оцениваемым параметрам (степенная, показательная, экспоненциальная и т. п. функции) индекс множественной корреляции не совпадает скоэффициентом множественной корреляции. Его называют «» и определяют как

                                        (9.149)

Коэффициенты (индексы) множественной детерминации получают, возводя коэффициенты (индексы) корреляции в квадрат, или по формулам.

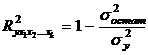                                                                                               (9.150)

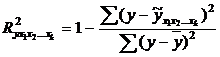                                                                             (9.151)

                                           (9.152)

 

Скорректированный индекс множественной детерминации

Индекс множественной детерминации используют для определения качества регрессии, чем больше , к единице тем выше качество подбора регрессии.

Но использование только одного индекса детерминации для определения наилучшего уравнения регрессии недостаточно. Необходимо учитывать, что при увеличении факторов включенных в уравнение регрессии, при одном и том же числе наблюдений , при расчете показателей корреляции, за счет использования остаточной дисперсии появляется систематическая ошибка – чем больше число параметров в уравнении регрессии, при одном и том же числе наблюдений , тем больше получается расчетный показатель тесноты связи. Если число факторов приближается к числу наблюдений, то расчетный показатель корреляции будет близок к единице, то есть показывать тесную связь, даже если связь незначительна. Для того чтобы избежать этого рассчитывают скорректированный индекс множественной детерминации.

                                                             (9.153)

или

                                                                         (9.154)

Скорректированный индекс множественной корреляции рассчитывают соответственно как:

                                                  (9.155)

или

                                                                    (9.156)

где:

- для линейной множественной модели – число факторов включенных в регрессионную модель. Для нелинейной модели - число параметров при  и их линеаризации (  и так далее), которое может быть больше числа факторов.

- число наблюдений.

В силу сказанного выше необходимо понимать, что нельзя перегружать множественную модель факторами, так как снижается достоверность расчетов, принято считать, что на каждые 8-10 наблюдений в модель целесообразно включать один фактор.

 

Частная корреляция

Множественный коэффициент (индекс) корреляции показывает тесноту связи между результатом и всеми включенными в модель факторами, для того, чтобы изучить силу связи между результатом и только одним из включенных в модель факторов, рассчитывают частные коэффициенты корреляции, для каждого из факторов включенных в модель.

Частный коэффициент корреляции показывает тесноту связи между результативным признаком и только одним фактором при элиминировании (устранении) влияния всех остальных включенных в модель факторов.

В зависимости от того, влияние скольких факторов необходимо исключать различают частные коэффициенты разных порядков: нулевого, первого, второго, третьего и т.д. Так, например:

· Коэффициенты частной корреляции нулевого порядка – коэффициенты парной корреляции, так как нет необходимости устранять влияние даже одного фактора.

· Коэффициенты частной корреляции первого порядка – коэффициенты частной корреляции, в которых элиминируется влияние одного фактора (, , и т.д.).

· Коэффициенты корреляции второго порядка – коэффициенты частной корреляции, в которых элиминируется влияние двух факторов (, , и т.д.) и так далее.

Коэффициенты частной корреляции более высоких порядков рассчитываются через коэффициенты корреляции более низких порядков. Коэффициенты первого порядка через коэффициенты нулевого порядка, второго порядка через коэффициенты первого порядка и т.д. Рекуррентная формула для расчета коэффициентов частной корреляции  порядка имеет вид:

            (9.157)

Коэффициенты частной корреляции могут принимать значения в пределах от -1 до 1.

Также частные коэффициенты корреляции можно рассчитать через множественные коэффициенты детерминации. Так коэффициент частной корреляции второго порядка рассчитывается как:

 или и т.д.                                     (9.158)

В общем виде уравнение для расчета коэффициентов частной корреляции  порядка имеет вид:

                                                             (9.159)

где

- коэффициент множественной детерминации  для всех факторов.

- коэффициент множественной детерминации без включения в модель фактора .

Рассчитанные через множественные коэффициенты детерминации частные коэффициенты корреляции могут принимать значения в интервале от 0 до 1.

Кроме того, частные коэффициенты корреляции можно рассчитать через . Так, например, частные коэффициенты корреляции первого порядка для двухфакторной линейной модели, выраженной в стандартизованном масштабе :

                                                                                       (9.160)

Отсюда:

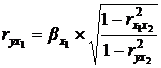 и                                                    (9.161)

Возводя в квадрат коэффициенты частной корреляции, получают коэффициенты частной детерминации.

Частные коэффициенты корреляции используют при формировании корреляционно-регрессионной модели, для отбора факторов. При этом из модели исключают факторы несущественные по критерию Стьюдента. 

Коэффициент частной детерминации показывает долю вариации результативного признака дополнительно сложившуюся при включении в модель фактора , в вариации признака, не объясненную включенными до этого в модель факторами. Можно рассчитать по формуле на основе коэффициентов множественной детерминации.

                                              (9.162)

где

- коэффициент множественной детерминации  для всех факторов.

- коэффициент множественной детерминации без включения в модель фактора .

Зная коэффициенты частной детерминации, последовательно нулевого, первого, второго и более высоких порядков, определяют коэффициент множественной корреляции.

(156)

 

Пример 9.21. По данным примера 9.20 необходимо рассчитать:

1. линейный индекс множественной корреляции, детерминации

2. линейные коэффициенты частной корреляции первого и второго порядков, детерминации.

Решение.

1. Рассчитаем индекс множественной корреляции по формуле:

В таблице 9.37 рассчитаем все возможные значения.

Таблица 9.37

№
1	10,49	0,408002	10,048113	0,195264
2	8,57	6,547202	9,601560	1,064116
3	10,95	0,031952	11,593826	0,414512
4	9,23	3,605252	8,633346	0,355996
5	11,97	0,707702	11,524121	0,198808
6	8,56	6,598477	8,887059	0,106968
7	12,18	1,105127	9,800000	5,664400
8	7,93	10,232002	7,427264	0,252743
9	15,75	21,355952	14,929855	0,672638
10	13,61	6,156602	11,502371	4,442100
11	13,99	8,186752	15,194027	1,449681
12	12,57	2,077202	13,414848	0,713768
13	10,93	0,039502	11,506605	0,332473
14	9,86	1,609727	9,461020	0,159185
15	7,39	13,978252	7,917362	0,278111
16	9,23	3,605252	9,804117	0,329610
17	15,40	18,243577	15,372985	0,000730
18	13,14	4,045127	13,824023	0,467887
19	13,12	3,965077	13,217642	0,009534
20	10,27	0,737452	10,512752	0,058929
21	9,12	4,035077	9,395289	0,075784
22	13,42	5,249827	12,140147	1,638024
23	10,29	0,703502	11,485126	1,428326
24	11,55	0,177452	11,101097	0,201514
25	15,26	17,067227	14,808601	0,203761
26	12,35	1,491452	12,305857	0,001949
27	8,24	8,344877	8,749497	0,259587
28	10,41	0,516602	10,573475	0,026724
29	9,62	2,276327	9,806811	0,034898
30	10,76	0,135977	10,532588	0,051716
31	8,35	7,721452	8,842748	0,242801
32	10,31	0,670352	10,941740	0,399095
33	9,38	3,058127	9,174913	0,042061
34	14,93	14,449502	13,502339	2,038216
35	12,46	1,772227	12,436891	0,000534
36	10,45	0,460702	10,534678	0,007170
37	12,38	1,565627	12,955222	0,330880
38	7,74	11,483627	9,872332	4,546840
39	14,49	11,298002	14,236792	0,064114
40	8,50	6,910327	7,582986	0,840915
Итого	445,150000	212,624438	445,152025	29,602363
В среднем	11,128750

 

Рассчитаем индекс множественной корреляции по формуле:

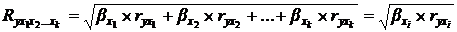
Значение стандартизованных коэффициентов регрессии и коэффициенты корреляции  из примера 21.

Индекс множественной корреляции  показывает, что между результативным признаком и всеми тремя включенными м модель факторами существует тесная связь (направление связи индекс множественной корреляции не определяет).

Индекс множественной детерминации:

Индекс множественной детерминации  показывает, что 86% вариации результативного признака обусловлено влиянием включенных в модель факторов.

Расчет множественного индекса корреляции  и множественного индекса детерминации 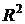 произведем в программе Microsoft Excel рассмотрен в примере 20, рисунок 9.

2. Рассчитаем частные коэффициенты корреляции по рекуррентной формуле:

Для этого воспользуемся матрицей парных коэффициентов корреляции из примера 9.20, (табл. 9.37).

Таблица 9.37

	Столбец 1 y	Столбец 2 x1	Столбец 3 x2	Столбец 4 x3	Столбец 5 x4
Столбец 1 y	1,000000
Столбец 2 x1	0,749996	1,000000
Столбец 3 x2	0,545459	0,188222	1,000000
Столбец 4 x3	0,731053	0,474013	0,466501	1,000000
Столбец 5 x4	0,640037	0,223318	0,549570	0,539163	1,000000

 

а) Рассчитаем частные коэффициенты корреляции и детерминации первого порядка.

· коэффициенты частной корреляции и детерминации первого порядка между результативным признаком  и фактором