Если предполагается, что величина результативного признака 
сложилась, в основном, под влиянием лишь одного факторного признака 
, при исследовании взаимосвязей между ними используют парную модель функции регрессии.
(9.19)
Для того чтобы, построить парную корреляционно-регрессионную модель необходимо решить следующие задачи:
1. отбор фактора,
2. спецификация модели (выбор вида функции регрессии).
Отбор фактора в модель парной регрессии
Фактор, который будет использован в парной модели, должен отвечать следующим требованиям: его влияние на результат должно быть таким, что влиянием всех остальных факторов можно пренебречь, но он не должен находиться в функциональной зависимости с результатом.
Число наблюдений фактора 
должно превышать число параметров при переменной в 6-7 раз. Так для модели вида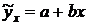 
необходимо не менее 6-7 наблюдений, а для модели 
потребуется не менее 12-14 наблюдений.
Спецификация модели парной регрессии
В парной регрессии используют линейные и нелинейные функции:
· 
– линейная функция
· 
– полином второй степени
· 
– полином третьей степени и т.д.
· 
– равносторонняя гипербола
· 
– степенная функция
· 
– показательная функция и т.д.
Выбор вида функции в модели парной регрессии может быть осуществлен следующими методами:
1. Графический метод. В его основу положено построение и исследование графика «корреляционное поле», на основании которого делается вывод о виде функции описывающей взаимосвязь между явлениями.
2. Аналитический метод. Опирается на изучение природы взаимосвязи между исследуемыми явлениями.
3. Экспериментальный метод. Вид функции подбирается экспериментально через анализ качества подбора функции, путем сравнения остаточной дисперсии рассчитанной для разных моделей.
Парная линейная регрессия
Парная линейная регрессия наиболее часто применяется в регрессионных моделях, в силу простоты расчета и интерпретирования результатов.
Расчет регрессионной модели данного вида заключается в нахождении уравнения вида:
(9.20)
или 
(9.21)
где;
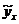- теоретическое значение результативного признака, рассчитанное по уравнению регрессии, показывающему взаимосвязь между и .
- фактическое значение результативного признака.
- случайная величина (возмущение, шум)
(9.22)
Показывает влияние не учтенных в модели факторов, а также случайных ошибок.
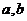- параметры уравнения.
Решение уравнения регрессии заключается в расчете его параметров. Наибольшее распространение из методов расчета параметров уравнения получил метод наименьших квадратов (МНК). МНК позволяет получать такие значения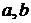 
, которые минимизируют сумму квадратов отклонений фактических значений от теоретических 
.
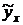(9.23)
При расчете параметров уравнения при помощи МНК необходимо решить систему из двух нормальных уравнений.
(9.24)
Также используют и готовые уравнения.
Для расчета параметра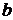 
:
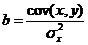; так как 
получим:
или 
(9.25)
где: 
(9.26)
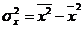(9.27)
Для расчета параметра 
:
(9.28)
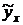Параметр - это теоретическое значение результативного признака при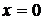 
и только в этом случае имеет экономический смысл, если 
параметр экономического смысла не имеет. В геометрическом представлении означает координату точки пересечения линии регрессии 
с осью ординат.
Параметр 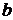называется коэффициентом регрессии. Коэффициент регрессии показывает, на сколько единиц, в среднем изменится результативный признак, если факторный признак увеличится на одну единицу. Например, если уравнение регрессии имеет вид:
где 
прибыль млн. руб. в месяц, а затраты на маркетинг тыс. руб. в месяц. Можно сказать, что при дополнительных затратах на маркетинг на 1 тыс. руб. прибыль в среднем возрастет на 0,02 млн. руб.
Геометрически это тангенс угла наклона прямой регрессии .
Пример 9.7. Имеются данные о средней прибыли (млн. руб.) и затратах на рекламу (млн. руб.) за декаду, по выборке, равной 15-ти предприятий сферы торговли (табл. 9.16).
Построить линейное уравнение регрессии.
Таблица 9.16.
| № |
|
|
| 1 | 37,8 | 0,3 |
| 2 | 38,0 | 0,5 |
| 3 | 39,0 | 0,7 |
| 4 | 37,5 | 0,8 |
| 5 | 39,5 | 0,9 |
| 6 | 36,8 | 1,1 |
| 7 | 40,0 | 1,3 |
| 8 | 40,1 | 1,6 |
| 9 | 40,0 | 1,7 |
| 10 | 39,0 | 2,2 |
| 11 | 38,0 | 2,5 |
| 12 | 41,0 | 2,6 |
| 13 | 41,6 | 2,7 |
| 14 | 41,0 | 3,0 |
| 15 | 41,9 | 3,2 |
Решение. Для расчета параметров уравнения регрессии используем МНК. МНК в данном случае дает систему уравнений:
1. Рассчитаем, в таблице 9.17 все возможные значения и подставим в систему.
После подстановки данных получим систему:
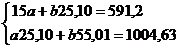
1) Решим систему методом исключения параметра . Для этого первое уравнение разделим на 15, а второе на 25,10.
Далее из второго уравнения вычтем первое
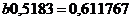
Рассчитаем коэффициент регрессии:
.
Подставим значение 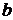в первое уравнение системы и рассчитаем параметр .
Таблица 9.17
| № |
|
| 
| 
| 
|
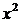
| 1 | 37,80 | 0,30 | 0,09 | 11,34 | 37,792344 |
| 2 | 38,00 | 0,50 | 0,25 | 19,00 | 38,028410 |
| 3 | 39,00 | 0,70 | 0,49 | 27,30 | 38,264476 |
| 4 | 37,50 | 0,80 | 0,64 | 30,00 | 38,382510 |
| 5 | 39,50 | 0,90 | 0,81 | 35,55 | 38,500543 |
| 6 | 36,80 | 1,10 | 1,21 | 40,48 | 38,736609 |
| 7 | 40,00 | 1,30 | 1,69 | 52,00 | 38,972676 |
| 8 | 40,10 | 1,60 | 2,56 | 64,16 | 39,326775 |
| 9 | 40,00 | 1,70 | 2,89 | 68,00 | 39,444808 |
| 10 | 39,00 | 2,20 | 4,84 | 85,80 | 40,034974 |
| 11 | 38,00 | 2,50 | 6,25 | 95,00 | 40,389074 |
| 12 | 41,00 | 2,60 | 6,76 | 106,60 | 40,507107 |
| 13 | 41,60 | 2,70 | 7,29 | 112,32 | 40,625140 |
| 14 | 41,00 | 3,00 | 9,00 | 123,00 | 40,979240 |
| 15 | 41,90 | 3,20 | 10,24 | 134,08 | 41,215306 |
| Сумма | 591,20 | 25,10 | 55,01 | 1004,63 | 591,199993 |
| В среднем | 39,413333 | 1,673333 | 3,667333 | 66,975333 | |
| 1,518713 | 0,931283 | 3,327158 | 38,874862 | |
|
| 2,306489 | 0,867289 | 11,069980 | 1511,254918 |
|
2. Рассчитаем параметры уравнения 
, используя готовые уравнения.
Небольшие расхождения в расчете параметров разными методами объясняются ошибками округления.
Подставим полученные значения (возьмем значения полученные в Microsoft Excel, как наиболее точные. см. далее) в уравнение регрессии .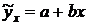
Коэффициент парной линейной регрессии 
показывает, что при увеличении фактора – «затраты на рекламу» на 1 единицу (1 млн. руб.), результат – «средняя прибыль» увеличится, в среднем на 1,180332 млн. руб.
Далее подставляя значения фактора в уравнение регрессии, рассчитаем теоретические значения 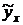, занесем их в последний столбик таблицы 9.17.
2) Рассмотрим решение данной задачи в Microsoft Excel.
Первое. В новой книге Microsoft Excel внесем исходные данные (рис 9.1).
Рисунок 9.1
Далее нажимаем кнопку Сервис и в открывшейся панели нажимаем кнопку Анализ данных.
В панели Анализ данных нажимаем Регрессия:
В панели регрессия вводим входной интервал , выделяя столбик, содержащий данные результативного признака, и входной интервал , выделяя столбик, содержащий данные фактора. Ответ можно поместить на новом рабочем листе, в новой рабочей книге, или на листе, содержащем условия выбирая выходной интервал, для чего указываем графа-клетку начала размещения ответа (рис 9.2).
Рисунок 9.2
Нажимаем ОК. Появится таблица, содержащая результаты регрессионного анализа (рис 9.3).
Рисунок 9.3
Параметр 
в данной таблице находится на пересечении столбика «Коэффициенты» и строки «Y-пересечение», параметр 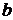- на пересечении столбика «Коэффициенты» и строки «Переменная Х1».
