Этот метод позволяет определить взаимосвязи между двумя и более признаками.
В ходе построения аналитической группировки необходимо решить следующие вопросы:
1. выбор факторных признаков
2. определение числа групп
3. оценка линии регрессии
4. измерения тесноты связи
Выбор факторных признаков
Выбор основывается на всестороннем анализе изучаемого явления, экономической теории, опыте и знаниях исследователя и т.д.
Определение числа групп
В принципе, чем больше число групп, тем точнее будет описана линия регрессии, но в месте с тем снижается точность расчета средних.
В данном вопросе необходимо, что бы увеличение числа групп, для более точного описания линия регрессии, не привело к утрате закономерного характера линии регрессии, из-за малочисленности групп.
Границы интервалов групп определяют, выделяя основные типы изучаемых явлений. При расчете величин интервалов возможно использование следующей формулы предложенной американским ученым Стерджессом.
 (9.9)
(9.9)
где:
 – максимальное значение признака в совокупности
– максимальное значение признака в совокупности
 – минимальное значение признака в совокупности
– минимальное значение признака в совокупности
N – число единиц в совокупности.
При разбиении изучаемой совокупности рекомендуется соблюдение принципа равных частот, т.е. образование групп с примерно одинаковой численностью единиц.
Оценка линии регрессии
Оценка линии регрессии в данном случае основывается на вычислении среднего значения признака  для интервала значений признака
для интервала значений признака  .
.
В качестве группировочного признака, как правило, используется факторный признак.
Показатель, характеризующий влияние факторного признака на результативный признак называется показателем силы связи  , который показывает, на сколько единиц изменится результативный признак, если факторный увеличится на одну единицу.
, который показывает, на сколько единиц изменится результативный признак, если факторный увеличится на одну единицу.
Если связь между признаками нелинейная, то есть, существенно изменяется при переходе от одной группе к другой, рассчитывается как:
 (9.10)
(9.10)
Так, например, если совокупность разбита на четыре группы, рассчитывают
1)  ; 2)
; 2)  ; 3)
; 3) 
где:
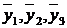 – средне-групповые значения результативного признака.
– средне-групповые значения результативного признака.
 – средние значения (или середины интервалов) факторного признака.
– средние значения (или середины интервалов) факторного признака.
Для группировочного признака, среднюю величину находят как середину интервала.
В случае линейной связи важным показателем является поазатель среднейсилы связи  .
.
 (9.11)
(9.11)
где:
 – средние значения результативного признака в последней и первой группах соответственно;
– средние значения результативного признака в последней и первой группах соответственно;
 – середины интервалов (или средние значения) факторного признака в последней и первой группах.
– середины интервалов (или средние значения) факторного признака в последней и первой группах.
Измерение тесноты связи
Измерение тесноты связи в аналитических группировках основано на правиле сложения дисперсий – общая дисперсия всегда равна сумме средней внутригрупповой и межгрупповой дисперсий:
 (9.12)
(9.12)
где:
 – общая дисперсия, характеризует вариацию признака во всей совокупности, сложившуюся под влиянием всех факторов и условий:
– общая дисперсия, характеризует вариацию признака во всей совокупности, сложившуюся под влиянием всех факторов и условий:
 или
или  (9.13)
(9.13)
где  – общая средняя.
– общая средняя.
 – средняя внутригрупповая дисперсия, оценивает вариацию признака, сложившуюся по влиянием других, неучтенных в данном исследовании факторов и независящую от фактора группировки. Она определяется как средняя из групповых дисперсий:
– средняя внутригрупповая дисперсия, оценивает вариацию признака, сложившуюся по влиянием других, неучтенных в данном исследовании факторов и независящую от фактора группировки. Она определяется как средняя из групповых дисперсий:
 или
или  (9.14)
(9.14)
 – внутригрупповая (случайная) дисперсия,
– внутригрупповая (случайная) дисперсия,
 или
или  (9.15)
(9.15)
где  – групповая средняя.
– групповая средняя.
 – межгрупповая (систематическая) дисперсия, измеряет систематическую вариацию, обусловленную влиянием фактора, по которому произведена группировка:
– межгрупповая (систематическая) дисперсия, измеряет систематическую вариацию, обусловленную влиянием фактора, по которому произведена группировка:
 (9.16)
(9.16)
Показателем тесноты связи между признаками в аналитической группировке служит корреляционное отношение:
 (9.17)
(9.17)
Корреляционное отношение может принимать значения от 0 до 1. Принято считать, что до 0,3 связь слабая, от 0,3 до 0,7 связь средняя, свыше 0,7 связь сильная. Чем больше корреляционное отношение, тем больше фактор, положенный в основание группировки, оказывает влияние на общую вариацию результативного признака, то есть они более тесно взаимосвязаны.
Квадрат корреляционного отношения – коэффициент детерминации:
 (9.18)
(9.18)
Показывает долю вариации результативного признака обусловленную включенным в модель фактором.
Пример 9.4. В таблице 9.9 приведены значения факторного признака  – затраты на рекламу млн.руб. и результативного признака
– затраты на рекламу млн.руб. и результативного признака  – прибыль млн. руб. и число предприятий в каждой группе
– прибыль млн. руб. и число предприятий в каждой группе  .
.
Таблица 9.9
Затраты на рекламу в месяц млн.руб. 
| Число предприятий, 
| Средняя прибыль за месяц млн. руб. 
|
| 0,08-0,12 | 10 | 23,56 |
| 0,12-0,16 | 15 | 25,20 |
| 0,16-0,20 | 8 | 29,80 |
| 0,20-0,24 | 5 | 36,50 |
Необходимо рассчитать показатели силы связи.
Решение.
Рассчитаем среднее значение фактора  как середину интервала, и изменение средней прибыли при переходе от одной группы к другой
как середину интервала, и изменение средней прибыли при переходе от одной группы к другой  . Результаты занесем в табл. 9.10.
. Результаты занесем в табл. 9.10.
Таблица 9.10
Затраты на рекламу в месяц млн.руб. 
| Число предприятий, 
| Средняя прибыль за месяц млн.руб. 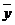
| Середина интервала млн.руб. 
| Изменение средней прибыли  млн.руб. млн.руб.
|
| 0,08-0,12 | 10 | 23,56 | 0,10 | - |
| 0,12-0,16 | 15 | 25,20 | 0,14 | 1,64 |
| 0,16-0,20 | 8 | 29,80 | 0,18 | 4,60 |
| 0,20-0,24 | 5 | 36,50 | 0,22 | 6,70 |
Изменение средней прибыли имеет существенные отличия при переходе от одной группы к другой, соответственно связь меду признаками нелинейная. Необходимо рассчитывать несколько показателей силы связи характеризующих взаимосвязи при переходе от одной группы к другой.
1)  ;
;
Это значит, что при увеличении затрат на рекламу от 0,08 до 0,16 млн. руб. средняя прибыль будет увеличиваться в среднем на 41 руб. на каждый дополнительно потраченный на рекламу рубль.
2)  ;
;
Это значит, что при увеличении затрат на рекламу от 0,16 до 0,20 млн. руб. средняя прибыль будет увеличиваться в среднем на 115 руб. на каждый дополнительно потраченный на рекламу рубль.
3)  .
.
Это значит, что при увеличении затрат на рекламу от 0,20 до 0,24 млн. руб. средняя прибыль будет увеличиваться в среднем на 167,5 руб. на каждый дополнительно потраченный на рекламу рубль.
Различия между показателями силы связи обусловлены тем, что сила влияния затрат на прибыль не постоянна, она возрастает при переходе от одной группы к другой.
Пример 9.5. По данным табл. 9.11 необходимо рассчитать показатели силы связи.
Таблица 9.11
Затраты на рекламу в месяц  млн.руб. млн.руб.
| Число предприятий, 
| Средняя прибыль за месяц 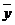 млн.руб. млн.руб.
| Середина интервала  млн.руб. млн.руб.
| Изменение средней прибыли  млн.руб. млн.руб.
|
| 0,08-0,12 | 10 | 23,56 | 0,10 | - |
| 0,12-0,16 | 15 | 25,20 | 0,14 | 1,64 |
| 0,16-0,20 | 8 | 26,86 | 0,18 | 1,66 |
| 0,20-0,24 | 5 | 28,51 | 0,22 | 1,65 |
Решение.
Изменения  отличаются не существенно, то есть связь между признаками линейная, рассчитаем показатель средней силы связи.
отличаются не существенно, то есть связь между признаками линейная, рассчитаем показатель средней силы связи.
 .
.
Это значит, что для всей совокупности, увеличение затрат на рекламу в среднем увеличит среднюю прибыль на 41,25 руб. на каждый дополнительно затраченный рубль.
Пример 9.6. Имеются данные о средней прибыли на отдельных торговых точках и профессиональном разряде продавцов (табл. 9.12)
Таблица 9.12
| Разряд | Средняя прибыль тыс.руб. 
| Число точек.

|
| Разряд | Средняя прибыль тыс.руб. 
| Число точек.

|
| I | 60 | 5 | I | 65 | 3 | |
| I | 68 | 7 | I | 68 | 4 | |
| II | 67 | 4 | II | 74 | 5 | |
| II | 75 | 3 | II | 67 | 4 | |
| II | 71 | 5 | II | 72 | 3 | |
| I | 70 | 5 | II | 69 | 4 |
1. Рассчитаем общую дисперсию выборки (табл. 9.13):


Таблица 9.13
| № | Средняя прибыль тыс.руб. | Число точек.
|
|
|
| |
| 1 | 60 | 5 | -8,673077 | 75,222265 | 376,111323 | |
| 2 | 68 | 7 | -0,673077 | 0,453033 | 3,171229 | |
| 3 | 67 | 4 | -1,673077 | 2,799187 | 11,196747 | |
| 4 | 75 | 3 | 6,326923 | 40,029955 | 120,089864 | |
| 5 | 71 | 5 | 2,326923 | 5,414571 | 27,072853 | |
| 6 | 70 | 5 | 1,326923 | 1,760725 | 8,803623 | |
| 7 | 65 | 3 | -3,673077 | 13,491495 | 40,474484 | |
| 8 | 68 | 4 | -0,673077 | 0,453033 | 1,812131 | |
| 9 | 74 | 5 | 5,326923 | 28,376109 | 141,880543 | |
| 10 | 67 | 4 | -1,673077 | 2,799187 | 11,196747 | |
| 11 | 72 | 3 | 3,326923 | 11,068417 | 33,205250 | |
| 12 | 69 | 4 | 0,326923 | 0,106879 | 0,427515 | |
| Итого |
| 52 |
|
| 775,44231 | |
| Среднее | 68,673077 |
|
|
| 14,912352 |
2. Рассчитаем дисперсию для каждой группы:
Таблица 9.14
| № | Средняя прибыль тыс.руб. | Число точек.
|
|
|
| |
| 1 | 60 | 5 | -6,375000 | 40,640625 | 203,203125 | |
| 2 | 68 | 7 | 1,625000 | 2,640625 | 18,484375 | |
| 3 | 70 | 5 | 3,625000 | 13,140625 | 65,703125 | |
| 4 | 65 | 3 | -1,375000 | 1,890625 | 5,671875 | |
| 5 | 68 | 4 | 1,625000 | 2,640625 | 10,562500 | |
| Итого |
| 24 |
| 303,625000 | ||
| Среднее | 66,375 |
| 12,651042 |
а) Группа с разрядом – I (табл. 9.14)

Таблица 9.15
| № | Средняя прибыль тыс.руб. | Число точек.
|
|
|
| |
| 1 | 67 | 4 | -3,642567 | 13,268294 | 53,073177 | |
| 2 | 75 | 3 | 4,357433 | 18,987222 | 56,961667 | |
| 3 | 71 | 5 | 0,357433 | 0,1277583 | 0,6387917 | |
| 4 | 74 | 5 | 3,357433 | 11,272356 | 56,361782 | |
| 5 | 67 | 4 | -3,642567 | 13,268294 | 53,073177 | |
| 6 | 72 | 3 | 1,357433 | 1,8426243 | 5,527873 | |
| 7 | 69 | 4 | -1,642567 | 2,6980263 | 10,792105 | |
| Итого |
| 28 |
|
| 236,42857 | |
| Среднее | 70,642567 |
| 8,4438776 |
б) Группа с разрядом равным II (табл. 9.15)
 .
.
3. Рассчитаем среднюю внутригрупповую дисперсию:
 .
.
4. Найдем межгрупповую дисперсию.

Проверим через правило сложения дисперсий

5. Рассчитаем корреляционное отношение:
 .
.
То есть, фактор, положенный в основу группировки (разряд) оказывает среднее влияние на результат (среднюю прибыль).
6. Рассчитаем детерминационное отношение

То есть вариация результативного признака на % обусловлена влиянием фактора – разряд продавца.












