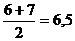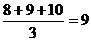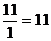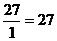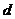В случае, когда имеются противоположные по значению варианты признака, говорят об альтернативном признаке (да, нет). Например, продукция может быть годной или не годной, животное может быть кошкой или не кошкой.
Для исследования взаимосвязей между двумя альтернативными признаками, то есть, вариация обоих атрибутивных признаков ограничена двумя группами, используют «тетрахорические показатели». Их расчет основан на использовании определенной расчетной таблицы (табл. 9.1).
Таблица 9.1
| II I | + | - |
| + | a | b |
| - | c | d |
Она состоит из четырех ячеек обозначенных буквами a, b, c, d – частоты, расположенные в I, II, III, IV квадрантах. Знаки 
и 
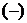в заголовках столбцов и строк характеризуют наличие или отсутствие альтернативного признака.
К «тетрахорическим показателям» относят:
· коэффициент ассоциации Пирсона
· коэффициент коллигации Юла
· коэффициент контингенции Юла и Кендэла
· коэффициент Шарлье и др.
Рассмотрим некоторые из них.
Коэффициент ассоциации Пирсона, данный коэффициент используют для измерения тесноты взаимосвязи надежности и годности. Рассчитывается по формуле:
(9.3)
Коэффициент коллигации Юла рассчитывается как:
(9.4)
Данный коэффициент показывает средний размер связи.
Рассмотренные коэффициенты могут принимать значения от 
до 
.
Если при измерении связи между качественными показателями образуется более двух групп, для определения тесноты связи используют:
· коэффициент взаимной сопряженности Пирсона
· коэффициент взаимной сопряженности Чупрова
· коэффициент взаимной сопряженности Крамера и. д.р.
Коэффициент взаимной сопряженности Пирсона рассчитывается:
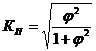(9.5)
Коэффициент взаимной сопряженности Чупрова рассчитывается:
(9.6)
где:
– число групп по первому и второму признаку соответственно.
– показатель взаимной сопряженности
Коэффициент взаимной сопряженности Чупрова целесообразно использовать, когда число групп по каждому признаку одинаково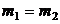 
. Если 
используют коэффициент Крамера.
Показатель взаимной сопряженности рассчитывают, используя вспомогательную таблицу (табл. 9.2)
Данные подставляют в формулу:
(9.7)
Таблица 9.2 - Вспомогательная таблица для расчета показателя взаимной сопряженности
| y x | I | II | III | Итого |
| I | … | … | 
| 
|
| II | … | … |
| |
| III | … | … |
| |
| Итого | 
|
|
| 
|
Коэффициент взаимной сопряженности Крамера рассчитывается:
(9.8)
где:
– минимальное, из значений 
и 
При 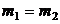значения коэффициентов Чупрова и Крамера совпадают.
Пример 9.1. По совокупности, состоящей из 27 предприятий, имеются данные о фондовооруженности тыс.руб. и производительности труда тыс.руб. (табл. 9.3).
Таблица 9.3
| № | 
| 
| № |
|
|
| 1 | 8,0 | 3 | 15 | 11,1 | 11 |
| 2 | 8,2 | 4 | 16 | 11,6 | 9 |
| 3 | 8,3 | 3 | 17 | 11,8 | 10 |
| 4 | 8,4 | 6 | 18 | 12,0 | 11 |
| 5 | 8,9 | 3 | 19 | 12,1 | 12 |
| 6 | 9,2 | 4 | 20 | 12,3 | 13 |
| 7 | 9,3 | 6 | 21 | 12,5 | 12 |
| 8 | 9,4 | 7 | 22 | 12,9 | 12 |
| 9 | 9,7 | 7 | 23 | 13,0 | 13 |
| 10 | 9,9 | 9 | 24 | 13,2 | 14 |
| 11 | 10,2 | 7 | 25 | 13,7 | 15 |
| 12 | 10,3 | 8 | 26 | 13,8 | 14 |
| 13 | 10,6 | 9 | 27 | 14,0 | 16 |
| 14 | 10,9 | 10 |
Необходимо определить направление и тесноту связи с помощью коэффициента Фехнера и коэффициента корреляции рангов Спирмена.
Решение.
I. Рассчитаем коэффициент Фехнера.
1. В таблице 9.4 рассчитаем отклонения значений признаков 
и 
от их средних значений – 
и 
, определим знак отклонений или 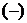и подсчитаем число совпадений (С) и несовпадений (Н) знаков отклонений.
Таблица 9.4
| № | x |
|
|
| С или Н |
| 1 | 8,0 | 3 | -2,9 | -6,2 | С |
| 2 | 8,2 | 4 | -2,7 | -5,2 | С |
| 3 | 8,3 | 3 | -2,6 | -6,2 | С |
| 4 | 8,4 | 6 | -2,5 | -3,2 | С |
| 5 | 8,9 | 3 | -2,0 | -6,2 | С |
| 6 | 9,2 | 4 | -1,7 | -5,2 | С |
| 7 | 9,3 | 6 | -1,6 | -3,2 | С |
| 8 | 9,4 | 7 | -1,5 | -2,2 | С |
| 9 | 9,7 | 7 | -1,2 | -2,2 | С |
| 10 | 9,9 | 9 | -1,0 | -0,2 | С |
| 11 | 10,2 | 7 | -0,7 | -2,2 | С |
| 12 | 10,3 | 8 | -0,6 | -1,2 | С |
| 13 | 10,6 | 9 | -0,3 | -0,2 | С |
| 14 | 10,9 | 10 | 0,0 | 0,8 | С |
| 15 | 11,1 | 11 | 0,2 | 1,8 | С |
| 16 | 11,6 | 9 | 0,7 | -0,2 | Н |
| 17 | 11,8 | 10 | 0,9 | 0,8 | С |
| 18 | 12,0 | 11 | 1,1 | 1,8 | С |
| 19 | 12,1 | 12 | 1,2 | 2,8 | С |
| 20 | 12,3 | 13 | 1,4 | 3,8 | С |
| 21 | 12,5 | 12 | 1,6 | 2,8 | С |
| 22 | 12,9 | 12 | 2,0 | 2,8 | С |
| 23 | 13,0 | 13 | 2,1 | 3,8 | С |
| 24 | 13,2 | 14 | 2,3 | 4,8 | С |
| 25 | 13,7 | 15 | 2,8 | 5,8 | С |
| 26 | 13,8 | 14 | 2,9 | 4,8 | С |
| 27 | 14,0 | 16 | 3,1 | 6,8 | С |
| Среднее | 10,9 | 9,2 |
|
|
|
2. Коэффициент Фехнера будет равен:
Коэффициент Фехнера показывает сильную положительную связь между признаками 
и .
II. Рассчитаем коэффициент корреляции рангов Спирмена.
1. Назначим ранги для показателя (табл. 9.5). Для этого ранжируем показатель 
по возрастанию и определим ранг, который признак занимает в ранжированном ряде.
а) Значение признака равное 3 занимает №1, №2 и №3, соответственно ранг данного значение будет 
.
б) Значение признака равное 4 занимает №4 и №5, соответственно ранг данного значение будет 
.
в) Значение признака равное 6 занимает №6 и №7, соответственно ранг данного значение будет 
.
г) Значение признака равное 7 занимает №8, №9 и №10, соответственно ранг данного значение будет 
.
д) Значение признака равное 8 занимает №11, соответственно ранг данного значение будет 
.
е) Значение признака равное 9 занимает №12, №13 и №14, соответственно ранг данного значение будет 
.
ж) Значение признака равное 10 занимает №15 и №16, соответственно ранг данного значение будет 
.
з) Значение признака равное 11 занимает №17 и №18, соответственно ранг данного значение будет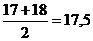 
.
и) Значение признака равное 12 занимает №19, №20 и №21, соответственно ранг данного значение будет 
.
к) Значение признака равное 13 занимает №22 и №23, соответственно ранг данного значение будет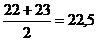 
.
л) Значение признака равное 14 занимает №24 и №25, соответственно ранг данного значение будет 
.
м) Значение признака равное 15 занимает №26, соответственно ранг данного значение будет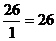 
.
н) Значение признака равное 16 занимает №27, соответственно ранг данного значение будет 
.
Таблица 9.5
| № | по возрастанию
| ранг признака
|
| 1 | 3 |
|
| 2 | 3 | |
| 3 | 3 | |
| 4 | 4 |
|
| 5 | 4 | |
| А | 1 | 2 |
| 6 | 6 |
|
| 7 | 6 | |
| 8 | 7 |
|
| 9 | 7 | |
| 10 | 7 | |
| 11 | 8 |
|
| 12 | 9 |
|
| 13 | 9 | |
| 14 | 9 | |
| 15 | 10 |
|
| 16 | 10 | |
| 17 | 11 |
|
| 18 | 11 | |
| 19 | 12 |
|
| 20 | 12 | |
| 21 | 12 | |
| 22 | 13 |
|
| 23 | 13 | |
| 24 | 14 |
|
| 25 | 14 | |
| 26 | 15 |
|
| 27 | 16 |
|
2. Назначим ранги для показателя ранжированием по порядку возрастания – 1; 2; 3;... 27 (табл. 6).
Далее в таблице 6 проставим ранги признаков и , рассчитаем разности рангов 
, квадраты разности рангов 
и сумму квадратов разностей рангов 
(табл. 9.6).
Таблица 9.6
| № |
|
|
|
|
|
|
| 1 | 8,0 | 3 | 1 | 2,0 | 1,0 | 1,00 |
| 2 | 8,2 | 4 | 2 | 4,5 | 2,5 | 6,25 |
| 3 | 8,3 | 3 | 3 | 2,0 | -1,0 | 1,00 |
| 4 | 8,4 | 6 | 4 | 6,5 | 2,5 | 6,25 |
| 5 | 8,9 | 3 | 5 | 2,0 | -3,0 | 9,00 |
| 6 | 9,2 | 4 | 6 | 4,5 | -1,5 | 2,25 |
| 7 | 9,3 | 6 | 7 | 6,5 | -0,5 | 0,25 |
| 8 | 9,4 | 7 | 8 | 9,0 | 1,0 | 1,00 |
| 9 | 9,7 | 7 | 9 | 9,0 | 0,0 | 0,00 |
| 10 | 9,9 | 9 | 10 | 13,0 | 3,0 | 9,00 |
| 11 | 10,2 | 7 | 11 | 9,0 | -2,0 | 4,00 |
| 12 | 10,3 | 8 | 12 | 11,0 | -1,0 | 1,00 |
| 13 | 10,6 | 9 | 13 | 13,0 | 0,0 | 0,00 |
| 14 | 10,9 | 10 | 14 | 15,5 | 1,5 | 2,25 |
| 15 | 11,1 | 11 | 15 | 17,5 | 2,5 | 6,25 |
| 16 | 11,6 | 9 | 16 | 13,0 | -3,0 | 9,00 |
| 17 | 11,8 | 10 | 17 | 15,5 | -1,5 | 2,25 |
| 18 | 12,0 | 11 | 18 | 17,5 | -0,5 | 0,25 |
| 19 | 12,1 | 12 | 19 | 20,0 | 1,0 | 1,00 |
| 20 | 12,3 | 13 | 20 | 22,5 | 2,5 | 6,25 |
| 21 | 12,5 | 12 | 21 | 20,0 | -1,0 | 1,00 |
| 22 | 12,9 | 12 | 22 | 20,0 | -2,0 | 4,00 |
| 23 | 13,0 | 13 | 23 | 22,5 | -0,5 | 0,25 |
| 24 | 13,2 | 14 | 24 | 24,5 | 0,5 | 0,25 |
| 25 | 13,7 | 15 | 25 | 26,0 | 1,0 | 1,00 |
| 26 | 13,8 | 14 | 26 | 24,5 | -1,5 | 2,25 |
| 27 | 14,0 | 16 | 27 | 27,0 | 0,0 | 0,00 |
| Итого |
|
|
|
|
| 77,00 |
3. Рассчитаем коэффициент корреляции рангов
Связь сильная.
Пример 9.2. Имеются данные о количестве торговых точек, сгруппированных по уровню средней прибыли и уровню квалификации продавцов в разных торговых точках (табл. 9.7).
Определить тесноту связи, через коэффициенты взаимной сопряженности.
Решение.
Рассчитаем показатель взаимной сопряженности непосредственно в таблице, используя формулу:
,
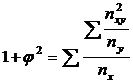1. Рассчитаем коэффициент Пирсона.
и из полученного значения 
(значение находится в нижнем правом углу таблицы) вычтем единицу:
2. Так как 
рассчитаем коэффициент Чупрова:
Коэффициент Чупрова всегда меньше чем коэффициент Пирсона.
3. Коэффициент взаимной сопряженности Крамера:
Так как значения коэффициентов Чупрова и Крамера совпадают.
Таблица 9.7
| Средняя прибыль Квалификация | Низкая | Средняя | Высокая | Итого |
| Низкий | 
| 
| 
| 
 
|
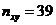
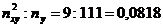
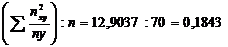
| Средний | 
| 
| 
| 
|
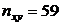
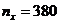
| Высокий | 
| 
| 
| 
|
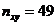
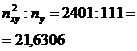
| Итого | 
| 
| 
| 
|
Пример 9.3. Группа предприятий, исследованная по влиянию на прибыль новой маркетинговой схемы, разделена на две подгруппы по надою.
Таблица 9.8
| Схема Прибыль | Переведены на новую схему | Не переведены |
| Прибыль увеличилась | 230 (а) | 84 (b) |
| Прибыль не увеличилась | 99 (c) | 210 (d) |
Рассчитаем коэффициент ассоциации Пирсона:
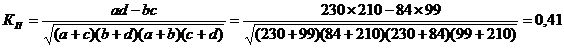
Полученное значение показывает среднюю, прямую связь между исследуемыми признаками.
Рассчитаем коэффициент коллигации Юла:
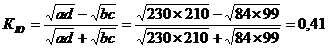
Полученное значение показывает, что средняя связь между исследуемыми признаками прямая, средняя.
