Оценивание результата измерений и его неопределенности проводится в следующей последовательности:
-составление уравнения измерений;
-оценка входных величин и их стандартных отклонений (неопределенностей);
-оценка измеряемой (выходной) величины и ее неопределенности;
- составление бюджета неопределенности;
-оценка расширенной неопределенности результата измерений;
-представление результата измерений.
Рассмотрим эти составляющие подробнее.
I. Составление уравнения измерения
В качестве основы для составления уравнения измерения используется классическое уравнение связи: зависимость Y = f (X 1, X 2,… Xk). Далее в результате анализа условий измерений и используемых СИ, устанавливаются другие факторы, влияющие на результат измерений, и они также включаются в уравнение связи в качествевеличин Xk +1, Xk +2,… Xm.
В итоге в рамках концепции неопределенности под уравнением измерения будет пониматься математическая зависимость между измеряемыми величинами X 1, X 2,… Xk, а также другими величинами, влияющими на результат измерения Xk +1, Xk +2,… Xm, и самим результатом измерения Y
(П2.1)
Величины X 1, X 2,… Xm можно считать входными величинами, используемые для оценивания неопределенности результата измерения, а результат измерения Y – выходной величиной измерения.
II. Оценка входных величин и их стандартных отклонений (неопределенностей)
Пусть имеются результаты n i измерений входной величины X i, где i = 1…m. Как известно, при нормальном распределении наилучшей оценкой этой величины является среднее арифметическое
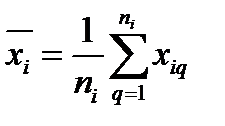(П2.2)
Стандартную неопределенность типа А определяют как среднеквадратическое отклонение по формуле:
(П2.3)
Для вычисления стандартной неопределенности по типу В используют:
-данные о предыдущих измерений величин, входящих в уравнение измерения;
- сведения, имеющиеся в метрологических документах по поверки, калибровки и сведения изготовителя о приборе;
- сведения о предполагаемом вероятностном распределении значений величин, имеющихся в научно-технических отчетах и литературных источниках;
- данные, основанные на опыте исследователя или общих знаниях о поведении и свойствах соответствующих (подобных) СИ и материалов;
- неопределенность используемых констант и справочных данных;
- нормы точности измерений, указанные в технической документации на методы и СИ;
- другие сведения об источниках неопределенностей, влияющих на результат измерения.
Неопределенности этих данных обычно представляют в виде границ отклонения значения величины от ее оценки. Наиболее распространенный способ формализации неполного знания о значении величины заключается в постулировании равномерного закона распределения возможных значений этой величины в указанных границах ± b i для i -ой входной величины. При этом стандартную неопределенность по типу В определяют по следующей формуле
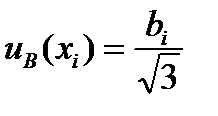(П2.4)
В случае других законов распределений формулы для вычисления неопределенности по типу В будут другие. В частности, если известно одно значение величины Xi, то это значение принимается в качестве оценки. При этом стандартную неопределенность вычисляют по формуле
(П2.5)
где Up – расширенная неопределенность, k – коэффициент охвата. Если коэффициент охвата не указан, то, с учетом имеющихся сведений, принимают предположение о вероятностном распределении неопределенности величины X i. Если такие сведения отсутствуют, то для определения коэффициента охвата можно воспользоваться данными таблицы П2.2 [П2.1].
Таблица П2.2
| Предполагаемое распределение неопределенности входной величины | Вероятность охвата Р, которой соответствует U (x i) | Коэффициент охвата k |
| Равномерное распределение | 0,99 – 1,0 | 1,71 - 1,73 |
| 0,95 | 1,65 | |
| Нормальное распределение | 1,0 (предел допускаемых значений) | 3 |
| 0,997 | 3 | |
| 0,99 | 2,6 | |
| 0,95 | 2 | |
| Неизвестное распределение | 2 |
Коэффициенты охвата для равномерного распределения, представленные в табл.П2.2, определены следующим образом. Для симметричных границ окончательного равномерного распределения СКО вычисляется по формуле (П2.4). Тогда расширенную неопределенность можно записать в виде 
. При расширенной неопределенности, соответствующей вероятности P =0,95 и границе равномерного распределения b =1, коэффициент k =0,95. 
= 1,65.
При расширенной неопределенности, соответствующей вероятности P =0,99, коэффициент k = 0,9995· = 1,71. При расчетах принималось, что =1,73 и площадь под равномерным распределением соответствует единице и, соответственно, при Р = 1коэффициент k =1,73.
Если известны граница суммы неисключенных систематических погрешностей, распределенных по равномерному (равновероятному) закону θ(Р) или расширенная неопределенность в терминах концепции неопределенности Up, то коэффициент охвата при числе неисключенных систематических погрешностей m >4, зависит от доверительной вероятности. Коэффициент охвата k равен1,1 при Р =0,95; и1,4 при Р =0,99 [П2.1].
Неопределенности входных величин могут быть коррелированны. Для вычисления коэффициента корреляции r (xi, xq) используют согласованные пары результатов измерений 
, где w = 1, 2,…, n ij; n ij – число согласованных пар результатов измерений 
Вычисления проводят по известной формуле из статистики и теории вероятности
(П2.6)
Значимость коэффициента корреляции определяется критерием отсутствия или наличия связи между аргументами.
III. Оценка измеряемой (выходной) величины и ее неопределенности
Оценку измеряемой величины y вычисляют как функцию оценок входных величин X 1, X 2,… Xm, по формуле (П2.1), предварительно внеся на все источники неопределенности, имеющие систематический характер, – поправки.
Вычисление суммарной неопределенности выходной величины проводят по тем же формулам, которые используются для расчета погрешностей косвенных измерений в классической концепции погрешности измерений.
В случае некоррелированных оценок входных величин, суммарную стандартную неопределенность 
вычисляют по формуле
(П2.7)
и в случае коррелированных оценок – по формуле
(П2.8)
где 
- коэффициент корреляции; 
- стандартная неопределенность i -ой – входной величины, вычисленная по типу А или типу В; 
- коэффициенты чувствительности выходной величины по отношению ко входной величине xi.
IV. Составление бюджета неопределенности
Под бюджетом неопределенности понимается формализованное представление полного перечня источников неопределенности измерений по каждой входной величине с указанием их стандартной неопределенности и вклада их в суммарную стандартную неопределенность результата измерений.
V. Оценка расширенной неопределенности результата измерений
Расширенная неопределенность равна произведению стандартной неопределенности u(y) результата измерений на коэффициент охвата k:
U (y) = k . u (y) (П2.9)
Руководство по неопределенности [П2.1] рекомендует рассматривать все результаты измерений при доверительной вероятности (вероятности охвата) Р =0,95. При этой вероятности преимущественно определяют число степеней свободы по эмпирической формуле Велча-Саттерствейта
(П2.10)
При этом коэффициент охвата определяется при вероятности Р =0,95 с использованием таблицы распределения Стьюдента по формуле
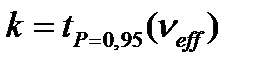, (П2.11)
Таблица 2П.3
Коэффициент охвата (
округлены до ближайшего целого числа)
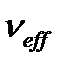
| 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 16 | 20 | 30 | 
|
| tP=0,95 | 3,182 | 2,776 | 2,571 | 2,447 | 2,365 | 2,306 | 2,262 | 2,228 | 2,120 | 2,086 | 2,042 | 1,960 |
| tP=0,99 | 5,841 | 4,604 | 4,032 | 3,707 | 3,499 | 3,355 | 3,250 | 3,169 | 2,921 | 2,845 | 2,750 | 2,576 |
Формулу для оценки суммарной стандартной неопределенности (П2.7) можно записать в более простом виде
, (П2.12)
также как и формулу (П2.10) для определения числа степеней свободы
, (П2.13)
где 
- число степеней свободы при прямых измерениях входной величины, n – число измерений, 
- оценка стандартных неопределенностей, вычисленных по типу А и по типу В, соответственно.
При оценке вклада неопределенности (см.формулу П2.10) по типу А принимают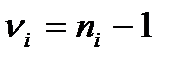 
, по типу В 
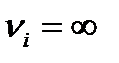. При этих условиях, легко показать из формулы (П2.10), что, если по типу А оценивается неопределенность только одной входной величины, то формула (П2.10) упрощается
, (П2.14)
где nA – число повторных измерений входной величины, оцениваемой по типу А.
VI. Представление результата измерений
При представлении результатов измерений Руководство рекомендует приводить достаточное количество информации, чтобы можно было проанализировать и/или повторить весь процесс получения результата измерений и вычисления неопределенностей, а именно:
- алгоритм получения результата измерений;
- алгоритм расчета всех поправок для исключения систематических погрешностей и их неопределенней;
- неопределенности всех используемых данных и способы их получения;
- алгоритмы вычисления суммарной и расширенной неопределенностей, включая значение коэффициента охвата k.
Таким образом, в документации по результатам измерений необходимо представлять:
uc – суммарную неопределенность;
Up – расширенную неопределенность;
k – коэффициент охвата;
ui – данные о входных величинах;
- эффективное число степеней свободы.
Например, если результатом измерения является электросопротивление, то при оформлениирезультата измерений, записывают: «Электросопротивление резистора составляет 163,2 Ом. Расширенная неопределенность результата измерений составляет ± 2,4 Ом при коэффициенте охвата равном 2» или «измерения показали, что электросопротивление резистора находится в интервале (160,8 – 165,6) Ом при коэффициенте, равном 2». По умолчанию предполагается, что эти результаты соответствуют вероятности охвата 0,95.
Несмотря на то, что нормативный документ РМГ 43-2001[П2.2] на территории России не действует (вместо него введен в действие ГОСТ Р 54500-2011 [П2.3]), приведенные в нем примеры очень понятны и могут дать необходимое представление о том, как проводить оценку неопределенности результатов измерений.
Пример из РМГ 43-2001
1) Приведем данные, имеющиеся в распоряжении оператора, задача которого состоит в измерении силы тока с помощью вольтметра и токового шунта.
1 Составление уравнения измерения
1.1Уравнение измерения
(1-П2)
где I – сила измеряемого тока, V – напряжение на шунте, которое непосредственно измеряется для определения силы тока, R – сопротивление шунта, t °C – температура окружающей среды, способная повлиять на результат измерения силы тока.
1.2. Производится многократное (n =10) измерение напряжения с помощью вольтметра на сопротивлении шунта при температуре t = (23,00±0,05)°С.
Границы неисключенной систематической погрешности вольтметра в милливольтах определены при его калибровке в виде следующего выражения:
q V = 3× 10-4× V + 0,02 (2-П2)
1.3. Сопротивление шунта определено при его калибровке для тока величиной I =10 А и температуре t =23,00°C и равно R 0 = 0,010 088 Ом. Относительные границы неисключеннойсистематической погрешности сопротивления шунта, установленные при его калибровке, равны
d q R = 0,070 % (3-П2)
Тогда при R = R 0 получают
q R = 7 × 10-4 × R 0 = 7,1×10-6Ом (4-П2)
1.4. Границы неисключенной систематической составляющей погрешности значения сопротивления шунта, обусловленной погрешностью измерений температуры, находят из формулы, определяющей зависимость сопротивления от температуры
R = R 0[1 + a(t – t 0)],
где R 0 – значение сопротивления при t = t 0 (t 0=23,00°C; R 0 = 0,010 088 Ом ); α – температурный коэффициент (a = 6∙10-6 К-1). В случае, когда границы погрешности измерения температуры составляют D t, границы соответствующей составляющей погрешности значения сопротивления равны
θ t , R =α∙D t · R (5-П2)
При D t =0,050С получают:θt,R = 3,0∙10-9 Ом или 3,0·10-5 %.
2 Нахождение результата измерений
В результате серии из n =10 измерений получают ряд значений Vi в милливольтах:
100,68; 100,83; 100,79; 100,64; 100,63; 100,94; 100,60; 100,68; 100,76; 100,65.
Среднеарифметическое вычисляют по формуле (П2.2)
мВ (6-П2)
Результат измерения силы тока получают по формуле
Ом
3 Анализ источников погрешности результата измерений
3.1. Среднеквадратическое отклонение (СКО), характеризующее случайную составляющую погрешности при измерениях напряжения 
, вычисляют по формуле (П2.3)
или 
(7-П2)
Примечания. 1) Значок d здесь и далее обозначает относительное значение величины.
2) В соответствии с рекомендациями Руководства симметричные интервалы не обозначаются значками ±.
3.2. Границы неисключенной систематической погрешности вольтметра в милливольтах при 
в соответствии с формулой (2-П2), будут равны
= 5,0× 10-2 мВ или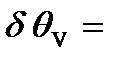 
0,050% (8-П2)
3.3. Границы неисключенной систематической погрешности сопротивления шунта, в соответствии с (3-П2) и (4-П2), установленные при его калибровке, равны
Ом или 
(9-П2)
3.4. Границы неисключенной систематической составляющей погрешности значения сопротивления шунта, обусловленной погрешностью измерений температуры в соответствии с (5-П2) равны
θ t , R = 3,0∙10-9 Ом или dθt,R = 3,0·10-5 % (10-П2)
В дальнейшем эту составляющую погрешности ввиду ее малости по сравнению с другими составляющими можно не учитывать.
4 Вычисление характеристик погрешности результата измерений
Для вычисления результирующей погрешности измерения, состоящей из случайной погрешности и суммы неисключенных погрешностей, используется формула, принятая в Государственной системе обеспечения единства измерений для косвенных измерений:
(11-П2)
где все составляющие погрешности определены при одной и той же доверительной вероятности Р. В числителе сумма доверительных границ случайной и суммарной неисключеннойпогрешности, в знаменателе - сумма СКО случайной и СКО суммарной неисключенной систематической погрешности, а 
- СКО суммарной погрешности измерения.
Примечание. Эта формула действительна при соотношении 
Если систематическая составляющая погрешности мала, т.е. 
< 0,8, формула (11-П2) упрощается 
С другой стороны, если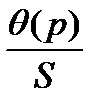 
> 8,0, то - 
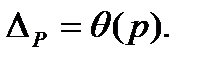Заметим, что для общности составляющие погрешности представляются в виде
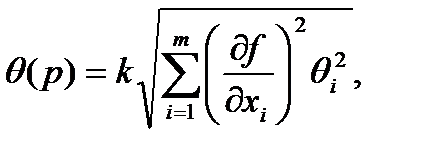
где k =1,1 при Р =0,95 и k =1,4 при Р =0,99 и m >4.
Ниже приводится вычисление всех составляющих погрешностей, входящих в формулу (11-П2).
4.1. Делается предположение о равномерном распределении неисключенных систематических составляющих погрешности результата измерений внутри их границ q V и q R . Тогда СКО суммарной неисключенной систематической составляющей погрешности результата измерений силы тока S q определяют по формуле
(12-П2)
или
d S q=0,050%
В этой формуле учтено, что коэффициенты влияния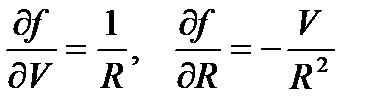 
4.2. Доверительные границы суммарной неисключенной систематической погрешности результата измерений силы тока q (р) при доверительной вероятности Р =0,95 оценивают по формуле
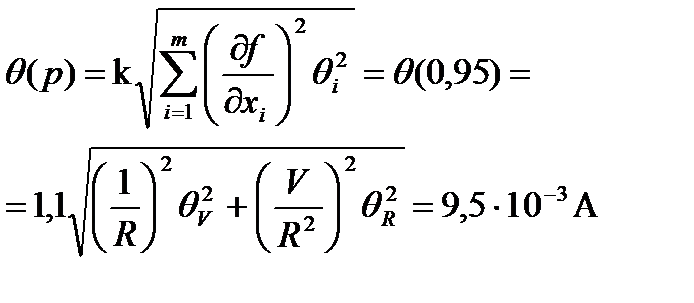(13-П2)
или dq0,95=0,095%
4.3. СКО случайной составляющей погрешности результата измерений силы тока S определяется по формуле
(14-П2)
4.4. СКО суммарной погрешности результата измерений силы тока будет равно
- (15-П2)
4.5. Доверительные границы погрешности результата измерений силы тока при вероятности 0,95 и эффективном числе степеней свободы 
, вычисленные по формуле (11-П2), дают результат
D0,95= 0,012 А или dD0,95= 0,12% (16-П2)
5 Вычисление неопределенности измерений
5.1. По типу А вычисляют стандартную неопределенность, обусловленную источниками неопределенности, имеющими случайный характер. Формула для вычислений подобна (7-П2)
мВ 
(17-П2)
Стандартную неопределенность силы тока, обусловленную источниками неопределенности, имеющими случайный характер, определяют по формуле
(18-П2)
5.2. По типу В вычисляют стандартные неопределенности, обусловленные источниками неопределенности, имеющими систематический характер. Закон распределения величин внутри границ считают равномерным.
Границы систематического смещения при измерениях напряжения, определенные при калибровке вольтметра, определяются соотношением (2-П2). Тогда соответствующую стандартную неопределенность uB , V вычисляют по формуле
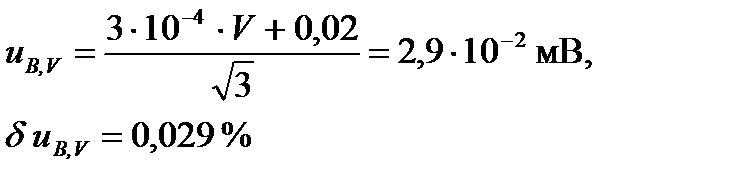(19-П2)
Границы, внутри которых лежит значение сопротивления шунта, определены при калибровке шунта и равны 7×10-4× R. Тогда при R = R 0 соответствующую стандартную неопределенность вычисляют по формуле
(20-П2)
Границы изменения значения сопротивления шунта, обусловленного изменением температуры, равны 
Соответствующую стандартную неопределенность получают в соответствии с формулой
(21-П2)
В дальнейшем этой составляющей неопределенности ввиду ее малости по сравнению с другими составляющими можно пренебречь.
Суммарную стандартную неопределенность uB, вычисленную по типу В, определяют по формуле
(22-П2)
5.3. Суммарную стандартную неопределенность uC вычисляют по формуле
(23-П2)
5.4. Эффективное число степеней свободы 
рассчитывают по формуле (10)
(24-П2)
5.5. Коэффициент охвата k находят по таблице 4 и определяют по формуле
(25-П2)
5.6. Расширенную неопределенность U 0,95 определяют следующим образом
(26-П2)
6 Сравнение результата вычислений различными методами
Сравнение результата вычислений погрешности измерений в доверительном интервале, соответствующем вероятности Р =0,95 и расширенной неопределенности с коэффициентом охвата равном двум, т.е. соответствующем уровню доверия 0,95. совпадают и равны 0,012 А.
Следует отметить, что это не случайно, поскольку в основе расчетов лежат одни и те же измерительные данные и одни те же подходы к распределениям различных переменных. Сравнения результатов измерений, определенных с помощью классического подхода и концепции неопределенности, как показано на многочисленных примерах в различных публикациях дают одни и те же окончательные результаты [П2.1, П2.2].
Однако результат, полученный в концепции неопределенности, трактуется иначе, чем результат, полученный при применении классического подхода. В концепции неопределенности не используются понятия истинного и действительного значений измеряемой величины. Результат измерения - вот что считается реальностью, поскольку величину истинного значения никто не знает. Расширенная неопределенность трактуется в Руководстве как интервал, содержащий заданную долю распределения значений, которые могли быть обосновано приписаны измеряемой величине.
Вообще расширенная неопределенность в концепции неопределенности не играет той роли, которая отводится в концепции погрешности. Считается, что основным результатом оценки является суммарная неопределенность uC, а расширенная неопределенность отличается от нее на постоянный коэффициент, который необходим в ряде специальных случаев для показа надежности оценки. Этот коэффициент может принимать значения от 2 до 3, при уровне доверия от 0,95 до 0,99.
Наши незнания об измеряемой величине определяются неопределенностью и группируются около результата измерения.
Список литературы, используемой в Приложении 2.
П2.1. А.Э. Фридман Основы метрологии. Современный курс. – С.-Пб.: НПО «Профессионал», 2008.
П2.2 РМГ 43-2001 Применение «Руководства по выражению неопределенности измерений», рекомендации по межгосударственной стандартизации, Межгосударственный совет по стандартизации, метрологии и сертификации, Минск, Изд-во стандартов, 2002
П2.3 ГОСТР 54500.1-2011/ Руководство ИСО/МЭК 98-1: 2009 Неопределенность измерения. Часть 1. Введение в руководства по неопределенностям измерения. – М.: Стандартинформ, 2012. – 17 с.
