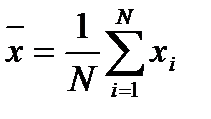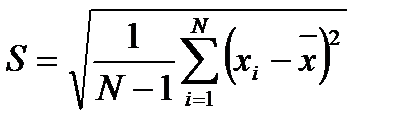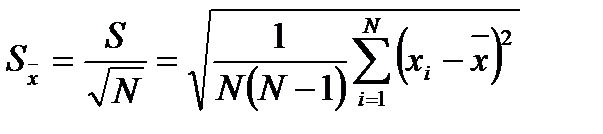В заключении подведем итог, чтобы человек, проводящий измерения и представляющий их результат, четко понимал всю последовательность операций (см. Таблицу 1.4). Измерения, проводимые на лабораторном практикуме, отличаются от измерений, проводимых, например, впервые (или высокоточных), поэтому в таблице для лабораторных работ выделен отдельный столбик.
Таблица 1.4.
Содержание этапов при проведении измерений
| № этапа | Вновь проводимые или метрологические измерения | Лабораторная работа |
| 1. | Уяснить задачу эксперимента и выбрать средства измерений с метрологическими характеристиками, отвечающими поставленной задаче (установить систематические погрешности средств измерений). | Определить цель и задачи проводимых измерений, ознакомиться со средствами измерения, используемыми в данной работе, установить их систематические погрешности. |
| 2. | Оценить оптимальное соотношение между точностью и временем для проведения измерений каждой измеряемой физической величины. | Определиться с количеством измерений n (чаще всего в лабораторных работах преподаватель требует провести 10 измерений). |
| 3. | Провести измерения каждой величины, стараясь реализовать условия максимальной идентичности и объективности. | |
| 4. | Определяют закон распределения результата измерения или проверяют нормальность этого закона. | Принимаем нормальный закон распределения результатов измерения. |
| 5. | Проводят точечные оценки законов распределения: среднее арифметическое всех результатов измерения:
СКО: СКО среднего арифметического значения:
| |
| 6. | Проводят проверку выскакивающих результатов на промах. | |
| 7. | Определяют доверительные интервалы для каждой измеряемой величины. Для этого задаются доверительной вероятностью (для обычных измерений P принимают равной 0,95; для высокоточных измерений P можно взять равной 0,99). Для данных n и P по таблице определяют значения коэффициента Стьюдента и определяют доверительный интервал: | |
| 8. | Определяют полную случайную погрешность для косвенных измерений | |
| 9. | Определяют суммарную погрешность результата (если такое суммирование можно провести),округляют полученную погрешность. | |
| 10. | Оформляют результат. Если можно суммировать случайную и систематическую погрешности, то результатзаписывают в виде интервала: y ± D y, при Р = 0,95 Если случайную и систематическую составляющие суммировать невозможно, то записывают полученное среднее арифметическое значение и все составляющие погрешностей. При необходимости строят график полученной функции. | |
В следующей главе пособия рассмотрен конкретный пример оформления отчета по лабораторной работе Физического практикума по механике.
1.
Контрольные вопросы к Главе 1.
1. Что представляет собой основное уравнение измерений?
2. Какие виды измерений бывают?
3. Назовите основные составляющие погрешностей.
4. Как обозначают классы точности средств измерений?
5. Какие основные законы распределений случайных величин использовались при обработке измерений?
6. Каковы точечные характеристики закона распределения?
7. Как переходят к интервальному представлению результата измерений?
8. Как рассчитать погрешность косвенных измерений?
9. Сформулируйте правила округления результата измерений?
10. Как надопредставлять результаты измерений?
Глава 2. Пример описания и оформления лабораторной работы по разделу «Механика»
2.1 Описание лабораторной работы № 4 «Измерение моментов инерции тел»
Цель работы: измерить величину момента инерции осесимметричных тела (коаксиального цилиндра) методом крутильных колебаний, провести сравнение измеренных значений с теоретическими предсказанными значениями момента инерции.
КРАТКАЯ ТЕОРИЯ.
1. Значение момента инерции тела относительно некоторой оси (осевого момента инерции) может быть рассчитано по формуле
, (2.1)
где r- плотность тела, а R - расстояние от от элементарного объема dV до оси.Вычислим с помощью этой формулы величину момента инерции коаксиального цилиндра высотой h, имеющего внутренний и внешний радиусы соответственно R1 и R2 относительно его оси симметрии (рис.2.1).
Направим ось Z системы координат вдоль оси симметрии цилиндра, а начало системы координат (точка 0) поместим на оси в середине высоты, т.е. в центре тяжести цилиндра. Разобьем коаксиальный цилиндр на тонкие диски высотой dz. На таком диске выделим узкий кольцевой слой радиусом R и шириной dR. В свою очередь на этом кольцевом слое выделим двумя радиусами, угол между которыми составляет малую величину d j, кольцевой сектор. Поскольку размеры этого сектора очень малы, мы не допустим большой ошибки, если его объем dV будем рассчитывать как объем куба со сторонами Rd j, dR и dZ. Таким образом, элементарно малый объем можно представить в следующем виде: d V=R.dR.d j. dZ.
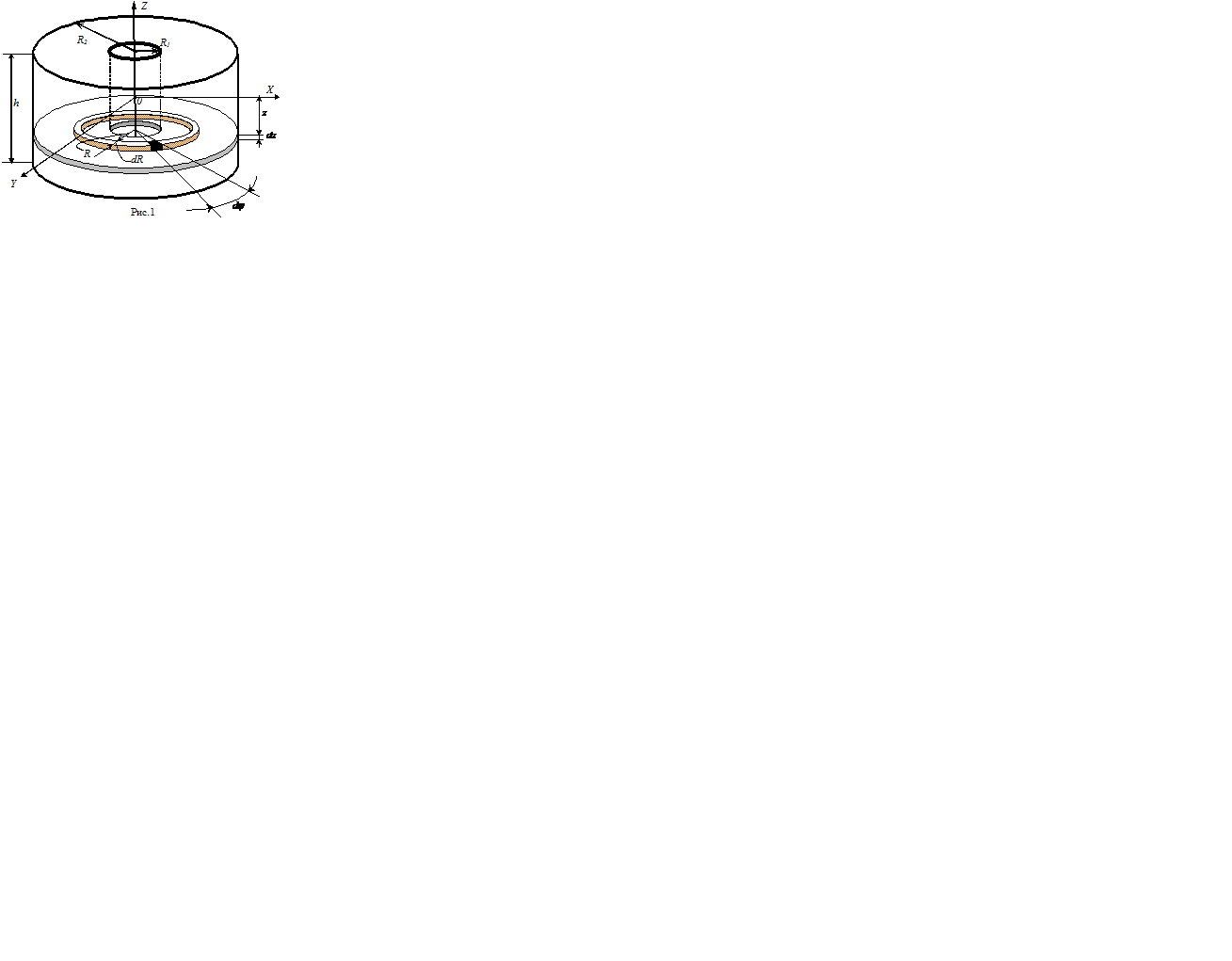
Рис. 2.1 Геометрия исследуемого образца
Интегрирование по всему объему цилиндра эквивалентно тройному интегрированию: поj в пределах от 0 до 2 p, по Z - в пределах от - h/2 до h/2, и по R в пределах от R1 до R2. Таким образом, интеграл (2.1) можно записать в следующем виде:
.
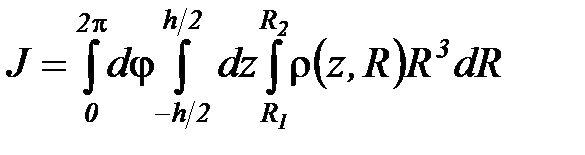Интегрирование по j дает просто множитель 2 p, то есть
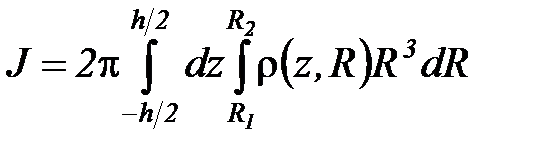
Если предположить, что тело однородно (r= Const), то после интегрирования по z и R, получаем
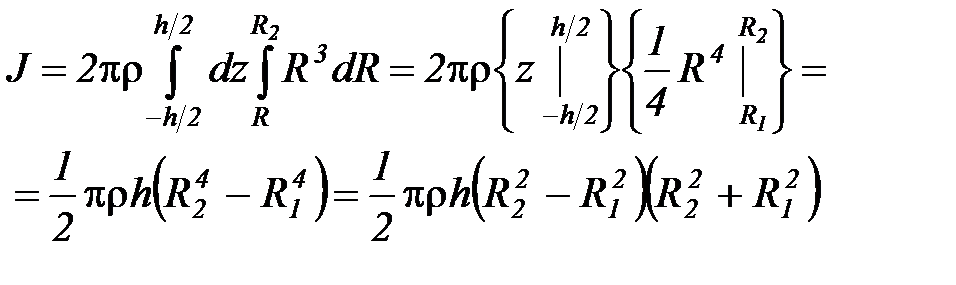
Но величина p (R 2 2 - R 1 2) - это площадь основания цилиндра, p (R 2 2 - R 1 2) h - это объем цилиндра, а p (R 2 2 - R 1 2) h r - это масса цилиндра M. Таким образом, для расчета момента инерции однородного коаксиального цилиндра получаем простую формулу:
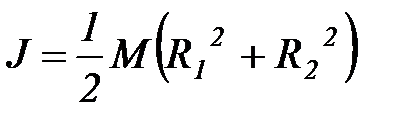. (2.2)
Итак, зная массу коаксиального цилиндра, а также его внутренний и внешний диаметр, можно определить его момент инерции относительно оси симметрии.
Необходимо отметить следующее обстоятельство. Формула (2.2) применима для определения величины момента инерции цилиндра только в том случае, если заранее известно, что цилиндр однороден. Такое предположение (об однородности) отсутствует в методе крутильных колебаний.
2. Расчет интеграла в формуле (2.1) достаточно прост для тел, обладающих некоторой симметрией. Для тел произвольной формы подобное интегрирование в общем случае невозможно. В этой ситуации для определения момента инерции можно воспользоваться наблюдением какого-либо движения, одна из характеристик которого известным образом зависит от момента инерции. В данной работе такой характеристикой является период крутильных колебаний. Метод крутильных колебаний позволяет определять значения моментов инерции для тел произвольной формы, имеющих произвольное распределение плотности по объему.
Крутильными колебаниями называют колебания, которые совершает тело, прикрепленное к стержню (или нити), если стержень (или нить) подвергнуть деформации кручения. Известно, что когда колебания совершает тело, подвешенное к пружине, подверженной деформации сжатия (растяжения), то тело в этом случае движется поступательно. Если деформации малы, т.е. справедлив закон Гука, то период таких колебаний Т определяется по формуле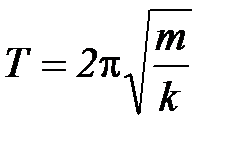 
, где m - масса тела и k - жесткость пружины при деформации сжатия (растяжения).
При крутильных колебаниях тело как бы совершает незавершенные вращения относительно некоторой оси. Поэтому в формулу для периода колебаний вместо массы входит момент инерции относительно оси вращения, а вместо жесткости k -жесткость по отношению к деформации кручения m. Таким образом, формула для периода крутильных колебаний приобретает вид
(2.3)
Связь между периодом колебаний и моментом инерции, задаваемая формулой (2.3), позволяет в принципе определить величину J из измерений периода Т, если известно значение m. Однако значение m обычно известно с невысокой точностью, поэтому способ измерения J, основанный на соотношении (2.3) имеет большую систематическую погрешность.
Систематическую погрешность измерений, обусловленную погрешностью m, можно исключить, если метод крутильных колебаний использовать для определения отношения моментов инерции тел прикрепленных к одной и той же нити. Очевидно, что это отношение не зависит от величины m. На самом деле, пусть к нити прикреплено некоторое тело, имеющее момент инерции относительно оси, совпадающей с осью вращения, равной J0. Период колебаний Т0 такого тела равен
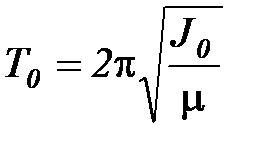
(2.4)
Если к первому телу прикрепить другое тело, момент инерции которого относительно оси вращения равен J, то момент инерции такой системы будет равен сумме J+J0. Соответственно изменится и период колебаний такой системы.
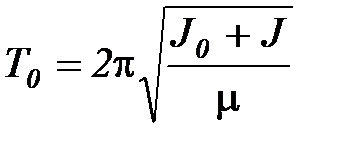(2.5)
Разделив (2.5) на (2.4), найдем 
. Отсюда
(2.6)
Из формулы (2.6) видно, что систематическая погрешность определения отношения J/J0 зависит только от систематических погрешностей измерения периодов колебаний Т и Т0, которые у современных секундомеров малы. Очевидно, что если величина J0 относительно оси вращения известна из каких-либо других соображений, то, вычислив соотношение J/J0 по формуле (2.6), легко определить момент инерции J относительно той же оси вращения.
МЕТОДИКА ЭКСПЕРИМЕНТА
Установка для измерения момента инерции методом крутильных колебаний представляет собой, собранные на массивном основании колонку для крепления исследуемых образцов и миллисекундомера. На колонке при помощи прижимных винтов размещаются три кронштейна. Верхний и нижний кронштейны имеют зажимы, Служащие для закрепления стальной проволоки, к которой подвешивается рамка с платформой в виде тонкого диска. Момент инерции рамки с платформой J0 относительно оси вращения известен. Его значение приведено на установке. Конструкция рамки такова, что позволяет размещать на платформе различные тела, момент инерции которых необходимо измерить. На среднем кронштейне закреплена стальная плита, которая служит основанием фотоэлектрическому датчику, электромагниту и угловой шкале. Электромагнит может изменять положение на плите, а его положение относительно фотодатчика показывает на угловой шкале стрелка, прикрепленная к электромагниту.
На лицевой панели миллисекундомера находятся:
- клавиша " Сеть " - включатель сети. Нажатие этой клавиши вызывает включение питающего напряжения. При этом на двух цифровых табло должны высвечиваться нули, а также должна гореть лампочка фотодатчика;
- клавиша " Сброс " - сброс секундомера. Нажатие этой клавиши вызывает сброс схем блока измерений и генерирование сигнала, разрешающего измерение;
- клавиша " Стоп " -окончание измерений. При нажатии этой клавиши генерируется сигнал на окончание счета времени;
-клавиша " Пуск " -управление электромагнитом. Нажатие этой клавиши вызывает отключение тока, питающего электромагнит.
На лицевой панели находится также два цифровых табло. На одном высвечивается число периодов колебаний рамки, на другом - время, в течение которого эти колебания совершаются.
При нажатии клавиши " Сеть " секундомер устанавливается в начальное состояние (нули на цифровых индикаторах) и блокируется схема формирования импульсов. Эта блокировка снимается сигналом, который вырабатывается при нажатии клавиши " Сброс ". Нажатие клавиши " Пуск " освобождает электромагнит, и начинаются крутильные колебания маятника. В момент первого прерывания светового потока, падающего на фототранзистор от лампочки, генерируется электрический импульс, который подключает к счетчику времени кварцевый генератор. Счетчик подсчитывает число импульсов, следующих с кварцевого генератора с частотой 10 кГц. Одновременно другой счетчик подсчитывает каждый (следующий после первого) нечетный импульс. Прохождение каждого такого нечетного импульса соответствует одному колебанию и показание цифрового табло счетчика периодов изменится на единицу.
При нажатии клавиши " Стоп " формируется сигнал, который подготавливает схемы к концу счета. Полностью счет прекращается в момент генерации очередного нечетного импульса фотодатчиком. При этом на цифровых табло высвечивается число колебаний и время, в течение которого они совершились. Систематическая погрешность измерения времени составляет 0,02 %.
Таким образом, методика измерения осевого момента инерции тела сводится к следующему. Вначале следует убедиться в применимости формулы (2.6), т.е. убедиться в том, что колебания слабо затухающие. После этого определить период колебания пустой платформы и платформы, с установленным на нее телом. Затем рассчитать J образца по формуле (2.6).
Описанный метод пригоден для определения момента инерции тела произвольной формы относительно оси колебаний. В частном случае, когда тело установлено на платформе так, что ось колебаний совпадает с осью симметрии тела, то методом крутильных колебаний определяется момент инерции относительно оси симметрии.
