Величины моментов инерции кольца, измеренные как методом крутильных колебаний, так и методом, использующим формулу (2.2), является результатами косвенных измерений. Получим формулы для расчета погрешности измерений величин D J, полученных этими методами. Для метода крутильных колебаний, в соответствии с правилами расчета погрешности косвенных измерений и формулой (6), получаем

Разделив обе части полученного выражения на J, получаем
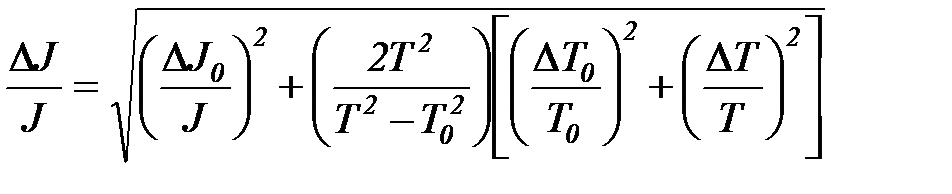 . (2.7)
. (2.7)
Подставляя в (2.7) вместо D J 0, D T 0 и D T вначале случайные, а затем систематические погрешности измеряемых впрямую величин, рассчитываются погрешности J, обусловленные соответственно случайными (D o J) и систематическими (D c J) погрешностями прямых измерений. Полная погрешность равна  .
.
Аналогично выводится формула и для расчета погрешности измерения методом, использующим формулу (2.5)

или  .(2.8)
.(2.8)
Так же, как и раньше, по формуле (2.8) рассчитываются погрешности, обусловленные случайными и систематическими погрешностями прямых измерений, а затем и полная погрешность.
После вычисления погрешностей можно провести корректное сравнение результатов измерения величин момента инерции, полученных разными способами. В том случае, если результаты измерений различаются на величину большую, чем погрешности эксперимента, необходимо сделать вывод о возможных причинах такого расхождения.
2.2 Пример оформления отчета по лабораторной работе по разделу «Механика»
Лабораторная работа № 4
«Измерение моментов инерции тел»
Цель работы: измерить величины момента инерции осесимметричных тел методом крутильных колебаний, провести сравнение измеренных значений с теоретически предсказанными значениями момента инерции.
1. Краткая теория:
Для определения момента инерции воспользуемся наблюдением какого-либо движения, одна из характеристик которого известным образом зависит от момента инерции. В данной работе такой характеристикой является период крутильных колебаний. Крутильными колебаниями называют колебания, которые совершает тело, прикрепленное к стержню (или нити), если стержень (или нить) подвергнуть деформации кручения.
При крутильных колебаниях тело совершает незавершенные вращения относительно некоторой оси. Таким образом, формула для периода крутильных колебаний приобретает вид
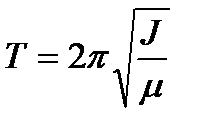 (1)
(1)
где J – момент инерции, m - деформация кручения.
Если к первому телу прикрепить другое тело, момент инерции которого относительно оси вращения равен J, то момент инерции такой системы будет равен сумме J + J 0. Соответственно изменится и период колебаний такой системы
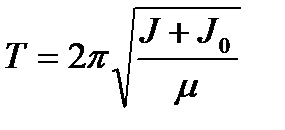 . (2)
. (2)
Систематическую погрешность измерений, обусловленную погрешностью m, можно исключить, если метод крутильных колебаний использовать для определения отношения моментов инерции тел прикрепленных к одной и той же нити. Поэтому получим
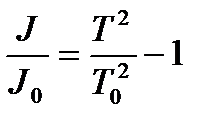 . (3)
. (3)
Из формулы (3) видно, что систематическая погрешность определения отношения J / J 0 зависит только от систематических погрешностей измерения периодов колебаний Т и Т0, которые у современных секундомеров малы.
Для момента инерции однородного кольца будем использовать формулу
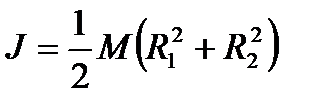 . (4)
. (4)
Итак, измерив массу кольца, а также его внутренний и внешний диаметр, можно определить момент инерции.
Необходимо отметить следующее обстоятельство. Формула (4) дает правильное значение момента инерции только в том случае, если точно известно, что кольцо однородное. В методе крутильных колебаний предположение об однородности кольца отсутствуют. Это значит, что метод крутильных колебаний позволяет определять значения моментов инерции для тел имеющих произвольное распределение плотности по объему.
Величины моментов инерции кольца, измеренные как методом крутильных колебаний, так и методом, использующим формулу (3), является результатами косвенных измерений. Для метода крутильных весов, в соответствии с правилами расчета погрешности косвенных измерений, получаем
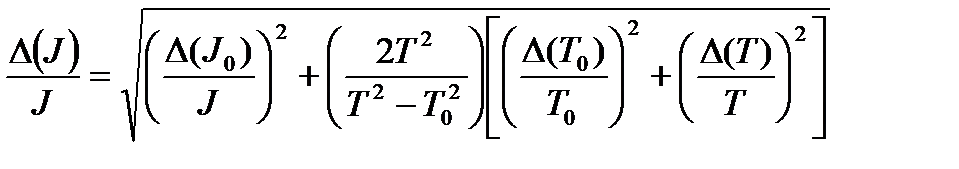 . (5)
. (5)
Подставляя в (5) вместо 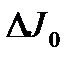 ,
,  и
и 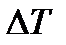 вначале случайные, а затем систематические погрешности измеряемых впрямую величин, рассчитываются погрешности J, обусловленные соответственно случайными и систематическими погрешностями прямых измерений. Полная погрешность равна
вначале случайные, а затем систематические погрешности измеряемых впрямую величин, рассчитываются погрешности J, обусловленные соответственно случайными и систематическими погрешностями прямых измерений. Полная погрешность равна
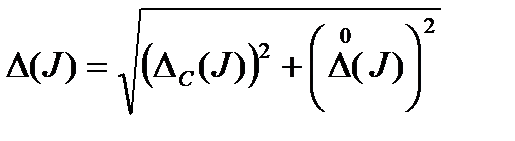 . (6)
. (6)
Формула для расчета погрешности измерения методом, использующим формулу (4)
 . (7)
. (7)
Так же, как и раньше, по формуле (7) рассчитываются погрешности, обусловленные случайными и систематическими погрешностями прямых измерений, а затем и полная погрешность.
Для вычисления среднего арифметического результатов наблюдения 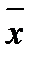 используем формулу
используем формулу
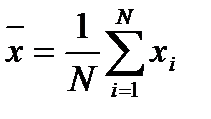 . (8)
. (8)
Для вычисления оценки среднего квадратического отклонения результата наблюдения  используем формулу
используем формулу
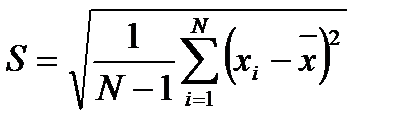 . (9)
. (9)
Для вычисления оценки среднего квадратического отклонения результата измерения 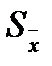 используем формулу
используем формулу
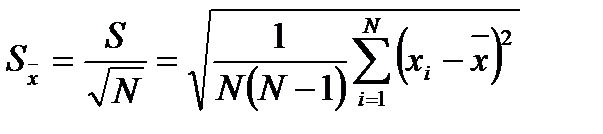 . (10)
. (10)
Доверительные границы случайной погрешности вычисляются по формуле
 (11)
(11)
где 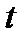 -коэффициент Стьюдента взятый из таблицы «Коэффициенты Стьюдента» с учетом количества проведенных измерений и доверительной вероятности (в данной работе Р =0,95).
-коэффициент Стьюдента взятый из таблицы «Коэффициенты Стьюдента» с учетом количества проведенных измерений и доверительной вероятности (в данной работе Р =0,95).
2. Приборы и оборудование:
A. Штангенциркуль Шц-1-150, согласно паспорту которого:
1) пределы измерений 0-150 мм;
2) цена деления нониуса 0,05 мм;
3) допускаемая погрешность ±0,004 мм.
B. Крутильный маятник с электронным цифровым секундомером, согласно паспорту которого:
1) момент инерции рамки с платформой равен (7,68±0,04)·10-4 кг·м2;
2) цена деления цифрового секундомера 1 мс;
3) допускаемая погрешность для цифрового секундомера 1 мс.
3. Ход работы:
3.1. Измерение момента инерции осесимметричного тела (кольца) методом крутильных колебаний.
3.1.1. Определение числа колебаний N, за которое амплитуда уменьшается в 2-3 раза.
А) пустая платформа.
| № п/п | Ni |
| 1 | >42 |
| 2 | >40 |
Б) платформа с установленным на нее кольцом.
| № п/п | Ni |
| 1 | >41 |
| 2 | >35 |
Так как число колебаний N >10, за которое амплитуда уменьшается в 2-3 раза, то колебания крутильного маятника являются слабо затухающими и следовательно можно использовать формулу (3) для расчета момента инерции кольца.
3.1.2. Определение периода колебаний пустой платформы.
| № п/п | t0i, с | Ni | T0i, с | 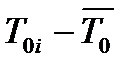 , ,
| 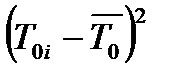 , с2 , с2
|
| 1 | 83,752 | 41 | 2,0427 | -0,000223 | 0,0000000501 |
| 2 | 30,643 | 15 | 2,0428 | -0,000088 | 0,0000000079 |
| 3 | 36,773 | 18 | 2,0429 | -0,000011 | 0,0000000001 |
| 4 | 14,302 | 7 | 2,0431 | 0,000187 | 0,0000000351 |
| 5 | 20,433 | 10 | 2,0433 | 0,000344 | 0,0000001187 |
| 6 | 30,644 | 15 | 2,0429 | -0,000022 | 0,0000000005 |
| 7 | 53,112 | 26 | 2,0427 | -0,000186 | 0,0000000347 |
| Σ |
|
| 14,301 | 0 | 0,0000002471 |
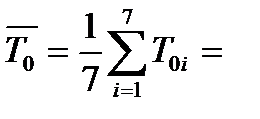 2,042955 с;
2,042955 с;
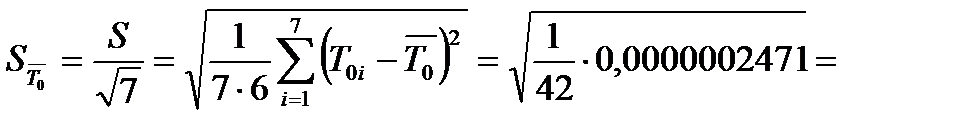 0,0000767 с;
0,0000767 с;
доверительный интервал для T 0: при n =7 и Р =0,95 находим t =2,45, по формуле (11) получим
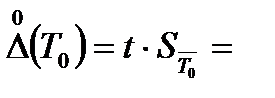 2,45·0,00008=0,000194 мм;
2,45·0,00008=0,000194 мм;
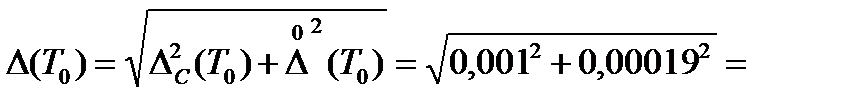 0,00102 с.
0,00102 с.
Ответ: 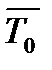 =(2,0430 ± 0,0010)с при Р =0,95.
=(2,0430 ± 0,0010)с при Р =0,95.
3.1.3. Определение периода колебаний платформы с исследуемым образцом.
| № п/п | ti, с | Ni | Ti, с | 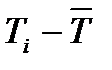 , с , с
| 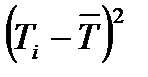 , с2 , с2
|
| 1 | 36,187 | 16 | 2,2616 | 0,04087 | 0,0016708679 |
| 2 | 37,652 | 17 | 2,2148 | -0,0059 | 0,0000358528 |
| 3 | 31,005 | 14 | 2,2146 | -0,00616 | 0,0000380491 |
| 4 | 90,755 | 41 | 2,2135 | -0,00727 | 0,0000529207 |
| 5 | 77,475 | 35 | 2,2135 | -0,00723 | 0,0000524150 |
| 6 | 55,342 | 25 | 2,213 | -0,00713 | 0,0000508547 |
| 7 | 42,061 | 19 | 2,2137 | -0,00707 | 0,0000500472 |
| Σ |
|
| 15,545 | 0 | 0,0019510074 |
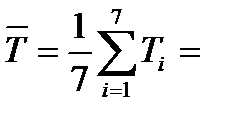 2,220811 с;
2,220811 с;
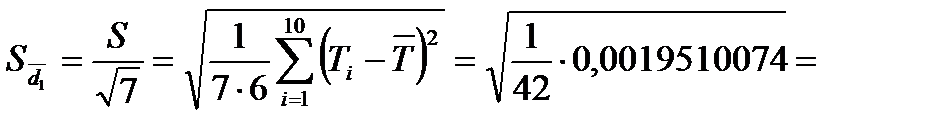 0,0068156 с;
0,0068156 с;
доверительный интервал для T: при n =7 и Р =0,95 находим t =2,45, по формуле (11) получим
 2,45·0,0068=0,01666 мм;
2,45·0,0068=0,01666 мм;
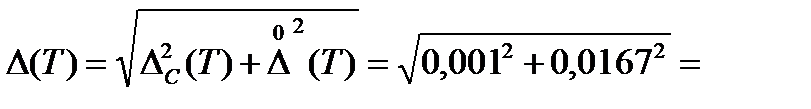 0,01673 с.
0,01673 с.
Ответ: 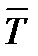 =(2,2208±0,0167) с при р=0,95.
=(2,2208±0,0167) с при р=0,95.
3.1.4. Вычисление момента инерции осесимметричного тела и погрешности его определения.
Для вычисления момента инерции воспользуемся формулой (3)
 1,3953·10-4 кг·м2.
1,3953·10-4 кг·м2.
Для подсчета погрешности используем формулу (5)


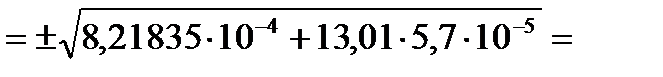 ±0,0394, следовательно,
±0,0394, следовательно,
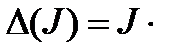 0,02877=±0,0401·10-4 кг·м2.
0,02877=±0,0401·10-4 кг·м2.
Ответ: J =(1,40±0,04)·10-4 кг·м2.
3.2. Расчет момента инерции осесимметричного тела (кольца) с помощью инструментальных измерений.
3.2.1. Определение массы кольца.
М =(151±1) г.
3.2.2. Измерение внутреннего диаметра кольца с помощью штангенциркуля с ценой деления нониуса 0,05 мм.
| № п/п |
|
|
|
| 1 | 38,00 | -0,115 | 0,013225 |
| 2 | 38,10 | -0,015 | 0,000225 |
| 3 | 38,05 | -0,065 | 0,004225 |
| 4 | 38,20 | 0,085 | 0,007225 |
| 5 | 38,20 | 0,085 | 0,007225 |
| 6 | 38,25 | 0,135 | 0,018225 |
| 7 | 38,00 | -0,115 | 0,013225 |
| 8 | 38,00 | -0,115 | 0,013225 |
| 9 | 38,15 | 0,035 | 0,001225 |
| 10 | 38,20 | 0,085 | 0,007225 |
| Σ | 381,15 | 0 | 0,085250 |
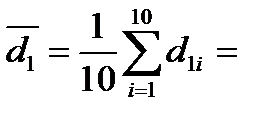 38,115 мм;
38,115 мм;
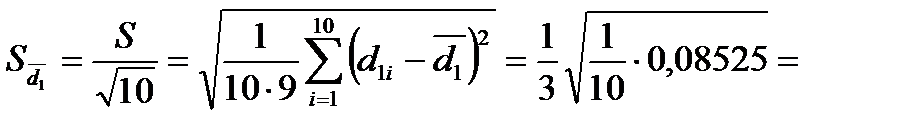 0,030777 мм;
0,030777 мм;
доверительный интервал для d1: при n =10 и Р =0,95 находим t=2,26, по формуле (11) получим
 2,26·0,031=0,07006 мм;
2,26·0,031=0,07006 мм;
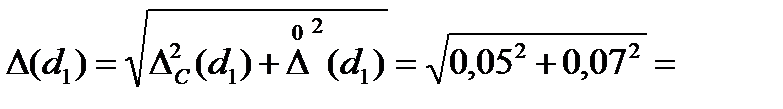 0,086 мм.
0,086 мм.
Ответ: 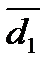 =(38,115±0,086) мм при Р =0,95.
=(38,115±0,086) мм при Р =0,95.
3.2.3. Измерение внешнего диаметра кольца с помощью штангенциркуля с ценой деления нониуса 0,05 мм.
| № п/п |
|
|
|
| 1 | 77,80 | -0,055 | 0,003025 |
| 2 | 77,90 | 0,045 | 0,002025 |
| 3 | 77,85 | -0,005 | 0,000025 |
| 4 | 77,95 | 0,095 | 0,009025 |
| 5 | 77,80 | -0,055 | 0,003025 |
| 6 | 77,85 | -0,005 | 0,000025 |
| 7 | 77,85 | -0,005 | 0,000025 |
| 8 | 77,80 | -0,055 | 0,003025 |
| 9 | 77,95 | 0,095 | 0,009025 |
| 10 | 77,80 | -0,055 | 0,003025 |
| Σ | 778,55 | 0 | 0,032250 |
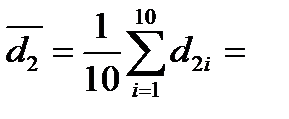 77,855 мм;
77,855 мм;
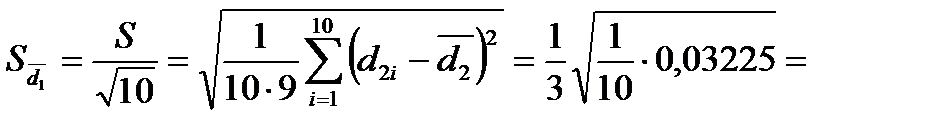 0,01893 мм;
0,01893 мм;
доверительный интервал для d 2: при n =10 и Р =0,95 находим t = 2,26, по формуле (11) получим
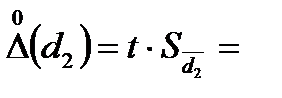 2,26·0,019=0,04294 мм;
2,26·0,019=0,04294 мм;
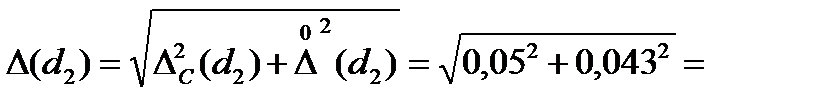 0,066 мм.
0,066 мм.
Ответ: 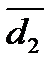 =(77,855 ± 0,066) мм при Р =0,95.
=(77,855 ± 0,066) мм при Р =0,95.
3.2.4. Вычисление момента инерции осесимметричного тела и погрешности его определения.
Для вычисления момента инерции используем формулу (4)
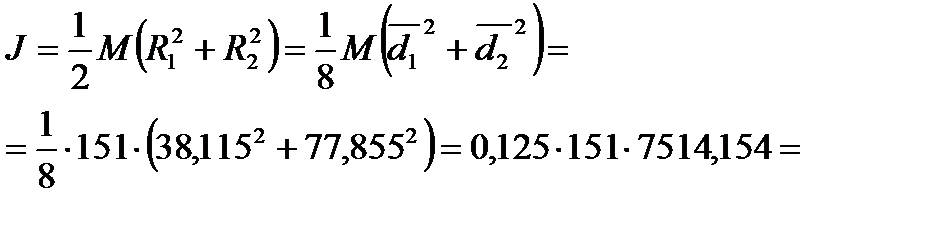
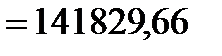 г·мм2=1,418·10-4 кг·м2.
г·мм2=1,418·10-4 кг·м2.
Для подсчета погрешности используем формулу (7)


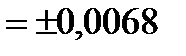 , следовательно,
, следовательно,
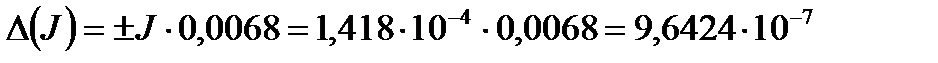 »10-6 кг·м2.
»10-6 кг·м2.
Ответ: J =(1,42±0,01)·10-4 кг·м2 при Р =0,95.
Вывод: значения момента инерции осесимметричного тела (кольца), измеренные методом крутильных колебаний, составляют (1,40±0,04)·10-4 кг·м2, что совпадает с значениями момента инерции, рассчитанного по инструментальным измерениям (1,42±0,01)·10-4 кг·м2. Следовательно, исследуемый образец является однородным.
Список литературы
1. РМГ 29 – 99 ГСИ. Метрология. Основные термины и определения
2. Тейлор Дж. Введение в теорию ошибок. – М.: Издательство «Мир», 1985. – 272 с.
3. Сергеев А.Г., Крохин В.В. Метрология. Карманная энциклопедия студента: Учебное пособие. – М.: Логос, 2001. – 375 с.
4. ГОСТ 8.417–2001 ГСИ. Единицы величин. – М.: Стандартинформ, 2001.
5. ГОСТ Р 8.736–2011 ГСИ. Измерения прямые многократные. Методы обработки результатов наблюдений. Основные положения. – М.: Стандартинформ, 2013. – 19 с.
6. ГОСТ 8.401–80 ГСИ. Классы точности средств измерений. Общие требования
7. Метрология, стандартизация, сертификация и электроизмерительная техника: Уч. пособие/под ред. К.К. Кима. – СПб.: Питер, 2006.
8. Краткие сведения по обработке результатов физических измерений./ Методические указания. Составитель Яковлев Г.П. – Екатеринбург: Изд-во Уральского университета, 2003 г.
9. МИ 1317-2004 ГСИ. Результаты и характеристики погрешности измерений. Формы представления. Способы использования при испытаниях образцов продукции и контроле их параметров
10. Теория измерений: Учеб.пособие/ Т.И. Мурашкина, В.А. Мещеряков, Е.А. Бадеева и др. – М.: Высш. шк., 2007. – 151 с.





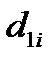 , мм
, мм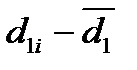 , мм
, мм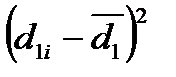 , мм2
, мм2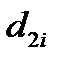 , мм
, мм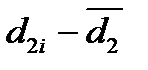 , мм
, мм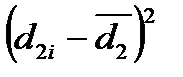 , мм2
, мм2
