В настоящем пособии мы будем работать исключительно с физическими величинами, которые можно измерить. Однако, есть физические величины, которые можно только оценить (например, цвет объекта по атласу цветов в колориметрии, твердость минералов по шкале твердости Мооса или силу землетрясений по шкале Рихтера). Также можно оценить каким-нибудь способом нефизические величины: коэффициент интеллекта, уровень знаний и т.п. Но нас будут интересовать только измеряемые физические величины.
Прежде чем начать измерение, необходимо выделить то физическое свойство данного объекта, которое будет определяться в конкретной измерительной задаче, также необходимо определить средство измерения, которое будет проградуировано в установленных единицах.
Основной смысл измерения будет заключается в так называемом основном уравнении измерения:
Х = q [ X ], (1.1)
где Х – измеряемая физическая величина, [ Х ] – единица измерения физической величины, q – количественное значение величины в установленных единицах измерения. Таким образом, результатом измерения является некоторое значение q в установленных единицах. Этот результат, конечно же, зависит от выбранных единиц измерения. Так, например, длина одного и того же объекта может составлять 10 дюймов и 25,4 сантиметров.
В действительности измерение одной и той же величины каждый раз происходит при различных условиях, и изменение их полностью определить невозможно. Поэтому каждый раз результат может получаться разным. Для дальнейшей обработки получаемых результатов необходимо воспользоваться определениями, данными в РМГ 29-99 «ГСИ. Метрология. Основные термины и определения»[1].
Истинное значение физической величины – это значение физической величины, которое идеальным образом характеризует в количественном и качественном отношении соответствующую физическую величину.
Действительное значение физической величины – значение физической величины, полученное экспериментальным путем и настолько близкое к истинному значению, что в поставленной измерительной задаче может быть использовано вместо него.
Результат измерения – значение величины, полученное путем ее измерения.
Чем ближе результат измерения к истинному значению, тем более качественно выполнено измерение. Однако на практике истинного значения никогда получить нельзя! Поэтому вместо него и используют действительное значение. Для количественного выражения качества проведенного измерения вводят понятие погрешности измерения: это разница между результатом измерения Х и истинным (в реальности действительным) значением Х и (или Х д):
D = Х - Х д, (1.2)
где D- обозначение абсолютной погрешности (это погрешность, выраженная в тех же единицах измерения, что и измеряемая величина).
По величине абсолютной погрешности трудно судить о точности проведенных измерений. Пусть были проведены два измерения напряжения с одинаковой абсолютной погрешностью, которая равна 0,1 мВ. Одно измерение U1 = 500 мВ, а второе U2 = 5 мВ. Качественно можно сказать, что первое измерение выполнено более точно. Поэтому для количественной оценки вводится понятие относительной погрешности.
Относительная погрешность – это погрешность, выраженная отношением абсолютной погрешности к действительному значению физической величины. Вот такой формулой она определяется:
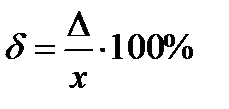(1.3)
Приведенная погрешность – это погрешность, выраженная отношением абсолютной погрешности к нормирующему значению:
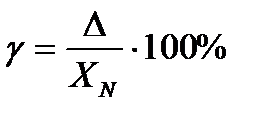(1.4)
где XN -нормирующее значение (что принимают в качестве нормирующего значения будет рассмотрено в разделе1.4).
Таким образом, по виду представления погрешности делятся на абсолютные, относительные и приведенные.
По характеру проявления погрешности можно разделить на случайные, систематические и промахи (грубые погрешности).
Систематическая погрешность (обозначается D С) – составляющая погрешности измерения, остающаяся постоянной или закономерно меняющаяся при повторных измерениях одной и той же физической величины. Составляющих данной погрешности может быть несколько. При проведении измерений иногда удается исключить некоторые составляющие (например, избавиться от влияния колебаний температуры при помощи термостатирования или можно экранировать магнитное поле). При проведении обработки результатов измерений рассматриваются только неисключенные систематические погрешности.
Случайная погрешность (
) – составляющая погрешности измерения, изменяющаяся случайным образом(как по знаку, так и по значению) в серии повторных измерений одной и той же физической величины, проведенных с одинаковой тщательностью в одних и тех же условиях. В них нет никакой закономерности, они неизбежны, неустранимы. Их присутствие выражается в виде разброса полученных результатов. Для их описания используется теория математической статистики.
Грубая погрешность – это случайная погрешность результата отдельного наблюдения, резко отличающаяся от остальных результатов (способы выявления таких погрешностей будут рассмотрены в разделе 1.7).
В зависимости от места возникновения различают инструментальные, методические и субъективные погрешности.
Инструментальная погрешность обусловлена погрешностью применяемого средства измерения.
Причинами возникновения методической погрешности могут быть следующие факторы:
- отличие принятой модели объекта измерения от модели, адекватно описывающей измеряемое свойство. Например, если при измерении площади поперечного сечения некоторой детали считают, что ее поперечное сечение имеет форму круга, а реально она может существенно отличаться от данного предположения. Проведение измерений диаметра в нескольких направлениях даст возможность скорректировать принятую модель.
-влияние средства измерения на объект. Этот фактор будет сказываться, например, при измерении напряжения: при подключении к участку цепи вольтметра, имеющего конечное значение внутреннего сопротивления, он будет шунтировать этот участок. При этом напряжение, которое будет показывать вольтметр, будет меньше реального значения.
- влияние алгоритмов (формул), применяемых при обработке результатов.
Субъективная погрешность измерения обусловлена, например, погрешностью отсчета оператором показаний по шкалам средства измерения. Эта погрешность может быть вызвана состоянием оператор, несовершенством органов чувств, эргономическими свойствами средств измерений. Таким образом, применение автоматических средств измерения позволит освободиться от субъективных погрешностей.
По влиянию внешних условий различают основную и дополнительную погрешности. Эти виды погрешности характеризуют погрешности средства измерения при работе в нормальных внешних условиях (основная погрешность) и при отклонении какой-либо влияющей величины от ее нормального значения (дополнительная погрешность). Например, нормальными значениями будут считаться температура 293 К, относительная влажность воздуха 60 %, плотность воздуха 1,2 кг/м3, частота питающей сети переменного тока 50 Гц. Эти значения указываются в паспорте средства измерения.
Чтобы перейти к расчетам погрешностей результатов измерений, надо рассмотреть какие бывают виды измерений, поскольку от этого зависит порядок обработки результатов и вычисление погрешностей.
1.3. Классификация измерений:
Измерения можно классифицировать по различным признакам. С точки зрения обработки полученных результатов важными являются две. Рассмотрим их.
1. По количеству измерительной информации измерения делятся на однократные и многократные [1]. Однократное – измерение, выполненное один раз (например, измерение времени по часам; или измерения, приводящие к разрушению объекта). Многократное измерение – измерение физической величины одного и того же размера, результат которого получен из нескольких следующих друг за другом измерений, т. е. состоящее из ряда однократных измерений. По ГОСТ Р 8.736 – 2011[5] многократными читаются измерения при n > 4.
2. По способу получения информации: прямые измерения, косвенные, совокупные,совместные
Прямое измерение – это измерение, при котором искомое значение физической величины получают непосредственно. Например, измерение длины детали при помощи штангенциркуля, измерение напряжения – вольтметром, измерение массы на весах. Для оценивания погрешности прямых измерений используют подходы, описанные в ГОСТ Р8.736 – 2011 ГСИ. Измерения прямые многократные. Методы обработки результатов измерений. Основные положения [5].
Косвенное измерение – это определение искомого значения физической величины на основании результатов прямых измерений других физических величин, функционально связанных с искомой величиной. Пример: определение плотности r тела цилиндрической формы по результатам прямых измерений массы m, высоты h и диаметрацилиндра d при помощи формулы:
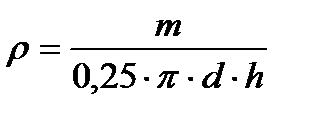(1.5)
Для того чтобы вычислить погрешность косвенных измерений, необходимо знать погрешность величин, измеряемых прямыми методами.
Совместные измерения – это измерения двух или нескольких неодноименных величин для нахождения зависимости между ними. Зависимость находят расчетным путем, путем решения системы уравнений, куда будут входить измеренные значения. Если зависимость предполагается линейной, то часто пользуются МНК (методом наименьших квадратов) (суть этого метода рассмотрена в разделе 1.10). Если же зависимость будет более сложная, то необходимо пользоваться компьютерными программами обработки результатов: например, Excel или Origin. Применение современных способов обработки результатов позволяет существенно упростить получение зависимостей в виде формул.
При совокупных измерениях одновременно проводят измерение нескольких одноименных величин. Искомую зависимость также определяют путем решения системы уравнений, получаемых при прямых измерениях различных сочетаний этих величин. Классическим примером такого вида измерений является определение массы отдельных гирь набора при помощи одной гири с заранее установленной массой (в метрологии для такой гири используется термин калиброванная) и по результатам прямых сравнений масс различных сочетаний гирь. Оценка погрешности при этом производится с использованием методов, применяемых для косвенных измерений.
Методы оценивания погрешностей результатов измерений мы начнем с систематических погрешностей, определяемых используемым средством измерения. Затем рассмотрим основные характеристики случайных погрешностей. Далее перейдем к погрешностям прямых измерений, после чего изложим порядок оценивания погрешностей косвенных измерений.
