Систематическая погрешность измерения определяется тем прибором, который используется в конкретном измерении: инструментальная погрешность. Метрологи и приборостроители существенно облегчили возможность определения данного вида погрешность при помощи такого понятия, как класс точности средства измерения. Он выражается в виде определенного числа и указывается или на шкале измерительного прибора или в его паспорте (технической документации). Нормативный документ, который регламентирует данный вопрос ГОСТ 8.401 - 80 [6].
ГОСТ 8.401 - 80 предусматривает выражение класса точности с помощью относительных чисел и абсолютных значений погрешности. В случае если класс точности выражается относительным числом, то это число выбирается из ряда
[ 1; 1,5; 2; 2,5; 4; 5; 6] · 10 n,
где показатель степени n может быть равен 1; 0; -1; -2 и т.д.
Обозначение класса точности зависит от характера систематической погрешности прибора: 1) аддитивный; 2) мультипликативный и 3) мультипликативный и аддитивный одновременно.
Рис. 1.1 Характер зависимости погрешности от измеряемой величины: а) аддитивный; б) мультипликативный, в) аддитивный и мультипликативный.
ГОСТ 8.401 - 80 устанавливает следующие способы обозначения классов точности.
1. Если характер погрешности – аддитивный (величина погрешности не зависит от измеренной величины рис. 1.1а), то на шкале прибора просто указано число из приведенного ряда, например 0,2. Это значит, что приведенная погрешность равна
g = ±0,2 %.
Как уже отмечалось выше, приведенной погрешностью называется отношение предела допускаемой основной погрешности к нормирующему значению измеряемой величины, т.е.
где D c - предел допускаемой основной погрешности; XN - нормирующее значение, выраженное в тех же единицах, что и D С.
Рис. 1.2Примеры выбора нормирующего значения: а - амперметр с равномерной шкалой с нулевым значением на краю шкалы, б - вольтметр с равномерной шкалой и нулевым значением внутри диапазона измерений
Нормирующее значение может выбираться по-разному:
а) для средств измерения с равномерной, практически равномерной или степенной шкалой, если нулевое значение лежит на краю шкалы или вне ее, нормирующее значение XN выбирается равным соответствующему пределу измерения (рис. 1.2,а); если нулевое значение лежит внутри диапазона измерений, то нормирующее значение выбирается равным большему из модулей пределов измерений (рис.1.2,б).
В случае, как на рис. 1.2, а нормирующее значение XN равняется60А. ТогдаD с = g . XN = 0,002. 60А = ±0,12 А.
При подсчетеD С приведенную погрешность g необходимо перевести из процентов в относительные единицы: 0,2 % = 0,002.
В случае, как на рис. 1.2,б нормирующее значение XN = 3Ви D С = ± 0,002 × 3В = ± 0,006В, так какï-2Вï<ï3Вï;
б) средствам измерений, для которых принята шкала с условным нулем, нормирующее значение устанавливается равным модулю разности пределов измерений. Например, для милливольтметра термоэлектрического пирометра с пределом измерений от 200 до 600°С XN = 600 -200 = 400°С;
в) для средств измерений с установленным номинальным значением нормирующее значение принимается равным этому номинальному значению. Например, для частотомера с диапазоном измерений от 45 до 55 Гц и номинальной частотой 50 Гц нормирующее значение XN = 50 Гц.
2. На шкале прибора указано число из приведенного ряда, подчеркнутое углом, например,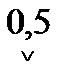 
. Шкала прибора существенно неравномерная. В этом случае также g = ± 0,5%, где g- приведенная погрешность. XN устанавливают равным всей длине шкалы или ее части, соответствующей диапазону измерения. Данные сведения можно уточнить можно по паспорту прибора.
3. Если характер погрешности – мультипликативный (см. рис. 1.1б), то на шкале прибора указано число из приведенного ряда, обведенное кружком. Например, на шкале нарисовано 1,0
В этом случае нарисованное число устанавливает относительную погрешность, выраженную в процентах: d = ± 1,0 %. Напомним, что относительной погрешностью называется отношение предела допускаемой основной абсолютной погрешностиDС к результату измерения X:
Пусть, например, предел измерения прибора 100 мА, при измерении стрелка отклоняется на 80 мА. В этом случае
D С = d . X = ±0,01× 80мА = ± 0,8мА.
Заметим, что значение d при расчетах надо перевести из процентов в относительные единицы.
4. Если погрешность имеет мультипликативный и аддитивный характер (см. рис. 1.1 в), то класс точности на приборе может быть выражен с помощью двух чисел из того же ряда, разделенных косой чертой. Например, на лицевой стенке прибора написано 0,02 / 0,01.В этом случае относительная погрешность вычисляется по формуле
(1.6)
где с = 0,02 %; d = 0,01; X K - больший (по модулю) предел измерений.
5. Для средств измерений, пределы допускаемой основной погрешности которых выражаются в форме абсолютных погрешностей,
D С = ± a илиD С = ± (a + b × . X), (1.7)
где a и b - положительные числа;
или в форме относительных погрешностей, причем последние установлены в виде графика, таблицы или формулы, отличной от рассмотренных выше, классы точности обозначают прописными буквами латинского алфавита или римскими цифрами, причем, чем ближе латинская буква к началу алфавита или цифра к нулю, тем меньше погрешность. В этом случае предел допускаемой основной погрешности прибора находят по паспорту прибора.
Заметим следующее: - средствам измерений с двумя или более диапазонами измерений одной и той же физической величины допускается присваивать два или более класса точности;- средствам измерений, предназначенным для измерения двух или более физических величин, допускается присваивать различные классы точности для каждой измеряемой величины.
Основная погрешность измерений - это погрешность, установленная для нормальных условий эксплуатации. Нормальные условия эксплуатации указываются в технической документации на средство измерений.
В пределах рабочих условий эксплуатации, если они выходят за пределы нормальных, кроме основной погрешности следует учитывать еще дополнительные погрешности. Сведения о них можно получить в технической документации на средство измерений.
На рис. 1.3 представлены фотографии конкретных приборов различных классов точности, о которых шел разговор выше. Это стрелочные аналоговые приборы и при работе с ними необходимо уметь правильно проводить измерения.
Рис. 1.3. Примеры представления класса точности на шкале прибора.
1. Необходимо знать цену деления шкалы. Для этого предел измерения X max надо разделить на количество делений N:
С = X max / N (1.8)
2. Чтобы провести правильный отсчет необходимо совместить изображение стрелки с ее изображением в зеркале.
а)
б)
Рис. 1.4. Проведение отсчета по шкале аналогового прибора: а) – неправильно; б) – правильно.
3. При записи результата необходимо умножить число делений n, которое показывает стрелка на цену деления C:
X = C . n. (1.9)
Рассмотрим конкретный пример средства измерения: микровеберметр Ф-190, предназначенный для измерения магнитного потока.
Рис. 1.5. Верхняя панель микровеберметра Ф-190.
Пусть предел измерения – 100 мкВб, показание при измерении составило n = 26 делений.
1. Определим цену деления: С = 100 мкВб: 50 делений = 2 мкВб/дел.
2. Тогда показания в микровеберах будет равно Ф = С ·n = 26 дел. . 2 мкВб/дел = 52 мкВб.
3. Определим систематическую погрешность по классу точности: g = 1,5 %. Нормирующее значение составляет 100 мкВб. Из формулы для приведенной погрешности (1.4) найдем абсолютную погрешность: DС = g· XN = 0,015 · 100 = 1,5 мкВб.
Если класс точности используемого средства измерений неизвестен, то в качестве систематической погрешности можно брать одно деление шкалы аналогового прибора или единицу последнего разряда цифрового прибора.
