Второй важный закон, использующийся в метрологии – нормальный закон распределения случайной величины:
Для этого закона распределения справедливы две аксиомы теории вероятностей:
1. Аксиома симметрии: при очень большом числе измерений случайные отклонения от среднего значения, равные по величине, но различные по знаку, встречаются одинаково часто.
2. Аксиома монотонного убывания плотности вероятностей: чаще всего встречаются меньшие отклонения, а большие отклонения встречаются тем реже, чем они больше.
Формула нормального закона распределения имеет следующий вид:
, (1.20)
где 
– среднее значение; s- среднее квадратическое отклонение. Общий вид дифференциальной и интегральной функций распределения для нормальных законов представлен на рис. 1.8.
Рис.1.8 Нормальный закон распределения плотности вероятности.
Точно также как в случае дискретных величин, для оценки законов распределения используют математическое ожидание М (х) и дисперсию D (x).
Математическое ожидание – положение случайной величины на числовой оси (среднее значение), определяющее центр распределения, вокруг которого группируются значения случайной величины. Для расчета используется следующая формула:
. (1.21)
Дисперсия (СКО в квадрате) служит для определения разброса получаемых результатов относительно среднего значения и определяется по формуле:
. (1.22)
Чем больше дисперсия, тем значительнее рассеяние результатов относительно среднего значения (см. рис. 1.9).
Рис.1.9. Законы нормального распределения относительно x ц=1,5 с различными СКО: 1 – 0,5; 2 – 1; 3 – 2; 4 – 5.
На практике все результаты измерений являются дискретными величинами, т. е. из всей генеральной совокупности (всех возможных значений) мы при измерении получаем некоторый ряд значений, который называется выборкой. Полученная выборка должна быть репрезентативной, т. е. достаточно хорошо представлять пропорции генеральной совокупности. Далее встает задача нахождения точечных оценок, характеризующих распределение величин, входящих в данную выборку. Эти оценки должны быть состоятельными (при увеличении объема выборки должны стремиться к истинному значению величины), несмещенными (математическое ожидание оценки равно оцениваемой числовой характеристике) и эффективными (иметь как можно меньшую дисперсию).
Точечной оценкой математического ожидания результата измерений является среднее арифметическое значение измеряемой величины:
. (1.23)
Точечная оценка дисперсии определяется по формуле:
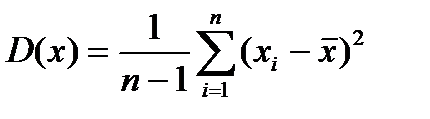. (1.24)
Формула для оценки среднего квадратического отклонения:
. (1.25)
Полученные оценки математического ожидания и среднего квадратического отклонения являются случайными величинами. Это проявляется в том, при повторении несколько раз серий из n наблюдений каждый раз будут получаться различные оценки 
и Sx. Рассеяние этих оценок принято оценивать СКОсреднего:
. (1.26)
Для практики важно на основе полученных точечных оценок определить доверительный интервал, в границах которого с доверительной вероятностью Р находится истинное значение измеряемой физической величины.
В метрологической практике используются квантильные оценки доверительного интервала. Под 100. Р -процентным квантилем x pпонимают абсциссу такой вертикальной линии, слева от которой площадь под кривой плотности распределения равна Р %, т. е. квантиль – это значение случайной величины (или ее погрешности) с заданной доверительной вероятностью Р. Например, математическое ожидание распределения является 50 %-ным квантилем x 0,5 (справа и слева относительно него вероятности равны 50 %). Между 25 %- и 75 %-ными квантилями заключено 50 % всех возможных значений случайной величины, а остальные 50 % лежат вне его. На основании такого похода вводят понятие квантильных значений погрешности, т. е. значений погрешности с заданной доверительной вероятностью Р – границ интервала ±D = (x p – x 1-P)/2: на его протяжении встречается Р % значений случайной величины, а q = 1- Р значений остаются за пределами их интервала.
При малом количестве наблюдений (n < 30) пользуются не нормальным законом распределения, а распределением Стьюдента. Оно описывает плотность распределения отношения:
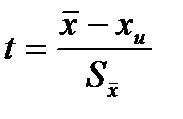. (1.27)
Вероятность того, что дробь Стьюдента в результате выполненных наблюдений примет некоторое значение в интервале от – t Pдо + t P можно рассчитать так:
, (1.28)
где k – число степеней свободы (n – 1). Коэффициенты Стьюдента табулированы (см. Табл. П1в Приложении 1). Поэтому с помощью распределения Стьюдента можно найти вероятность того, что отклонение среднего арифметического от истинного значения измеряемой величины не превышает следующей величины:
. (1.29)
