Неразветвленные цепи переменного тока

§ 12.1. Цепь с активным сопротивлением и индуктивностью

Векторная диаграмма тока и напряжений. Реальная катуш­ка любого электротехнического устройства имеет два параметра: активное сопротивление r и индуктивность L.Поэтому в схеме замещения реальную катушку можно представить активным r и реактивным Lэлементами, соединенными последовательно (рис 12.1). Явления, происходящие в реальной катушке, те же, что и в цепи рис. 12 1. Мгновенное значение тока в цепи с после­довательным соединением активного сопротивления г и индуктив­ности Lзависит не только от приложенного напряжения и, сопротивления г, но и от возникающей в цепи ЭДС само­индукции 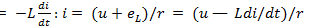.Отсюда +  Первое слагаемое напряжение активным напряжением, а второе 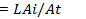— реактивным. Активное напряжение преодолевает активное сопротивление r,а реактивное 1 уравновешивает ЭДС     самоиндукции e_L.Согласно выводам, получаемым в § 11.1 и 11.2, активное напряжение совпадает по фазе с током, а реактивное опережает ток на90°. Это положение необходимо учесть при построении вектор­ной диаграммы цепи (рис. 12.2,а). За исходный вектор прини­мают вектор тока I который совмещают с положительным направлением оси абсцисс (при начальной фазе Ψ = 0). Вектор активного напряжения 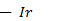откладывают по направлению вектора токам I, а вектор реактивного (индуктивного) напряже­ния 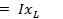проводят под углом +90° к вектору тока I.

Таким образом, векторы напряжений U_a, U_L. и U образуют прямоугольный треугольник, называемый треугольником напря­жений. Из векторной диаграммы видно, что напряжение Uна за­жимах катушки опережает по фазе ток I на угол ср. Величину этого угла можно определить из выражения .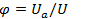

 

 

2.Полное сопротивление цепи. Из треугольника напряжений, пользуясь теоремой Пифагора, определим напряжение на зажимах катушка: 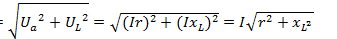 Отсюда ток в цепи

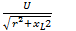                                 (12.1)

 

Это отношение выражает закон Ома. Величина 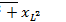 назы­вается полным сопротивлением цепи и обозначается z.Таким образом, полное сопротивление

                              (12.2)

а ток

                                  (12.3)

Активное, индуктивное и полное сопротивления связаны меж­ду собой таким же соотношением, как стороны прямоугольного треугольника (рис. 12.2,6); r и x_L — катеты этого треугольника, az— гипотенуза. Треугольник сопротивлений можно получить, если все стороны треугольника напряжений (рис. 12.2, а) умень­шить в I раз. Действительно, U/I=z; U_a/I = r\ Ul/I =x_L.Соп­ротивления цепи постоянны, поэтому их нельзя изображать векторами.

3.Активная, реактивная и полная мощности. Умножим сто­роны треугольника напряжений (рис. 12.2, а) на ток в цепи I. В результате получим подобный треугольник, стороны которого соответствуют мощностям (рис. 12.2, в). Первый катет треуголь­ника мощностей изображает активную мощность цепи

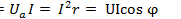,                          (12.4)

а второй — реактивную

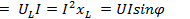.                         (12.5)

 

Гипотенуза треугольника мощностей изображает полную мощность

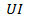.                                                     (12.6)

Полная мощность — характерная величина генераторов, трансформаторов и других электрических устройств. Единицей полной мощности в СИ является вольт-ампер (В·А). Более крупной единицей является киловольт-ампер (кВ·A): 1 кВ·А — = 10³ В·А. Формулы (12.4) — (12.6) справедливы для вычисле­ния соответствующих мощностей в любой цепи переменного тока.

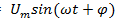4.Графики мгновенных значений тока, напряжения и мощ­ности. Напряжение на зажимах катушки Uопережает по фазе ток I на угол φ, поэтому фаза напряжения должна быть большефазы тока на угол φ. Если мгновенное значение тока в ка­тушке  то напряжение . Мгновенная мощность цепи р=ш. На рис. 12.3 даны графики тока, напряжения и мощности. Мгно­венная мощность равна нулю в те моменты времени, когда равны нулю напряжение и или ток i.Если напряжение и ток имеют одинаковые знаки, мгновенная мощность положительна. В это время цепь получает энергию от генератора. В те части периода, когда напряжение и ток имеют разные знаки, мгновенная мощ­ность отрицательна. При этом некоторая часть энергии возвра­щается генератору.

 

§ 12.2. Цепь с активным сопротивлением и емкостью

1.Векторная диаграмма тока и напряжений. В § 11.4 рассмот­рена цепь с емкостью (идеальный конденсатор). В действитель­ности любой конденсатор обладает потерями, т. е. активной мощностью Р. Поэтому реальный конденсатор можно предста­вить схемой последовательного соединения активного сопротив­ления г и емкостного сопротивления х_с (рис. 12.5). Сопротивле­ние r определяется мощностью потерь: . Напряжение цепи и в любой момент времени состоит из двух слагаемых: u = u_a + u_c - Активное напряжение и_а совпа­дает по фазе с током в цепи i,а емкостное u_c отстает по фазе от тока на 90°. Дейст­вующие значения слагаемых напряжения: U_а = Ir, Uc= Ix_c= I /( ωC). Для опреде­ления действующего значения напряжения Uпостроим векторную диаграмму. Пост­роение диаграммы (рис. 12.6, а) начнем Рис. 12.5с вектора тока I, отложив его горизонтально. Вектор активного падения напряжения U_а отложим по нап­равлению вектора тока I, а вектор емкостного падения напряже­ния Ucповернем относительно вектора тока на 90° по ходу часо­вой стрелки. Сложим векторы напряжений U_aи Uc,получим вектор напряжения U.Векторы напряжений U_a, Ucи Uобра­зуют прямоугольный треугольник. Из векторной диаграммы вид­но, что напряжение на зажимах цепи отстает по фазе от тока на угол ф. Абсолютную величину этого угла можно определить из выражения cosφ = U_a / U.

2.Треугольники сопротивлений и мощностей. Все стороны треугольника Напряжений уменьшим в I раз. В результате получим треугольник сопротивлений (рис. 12.6)

 

 

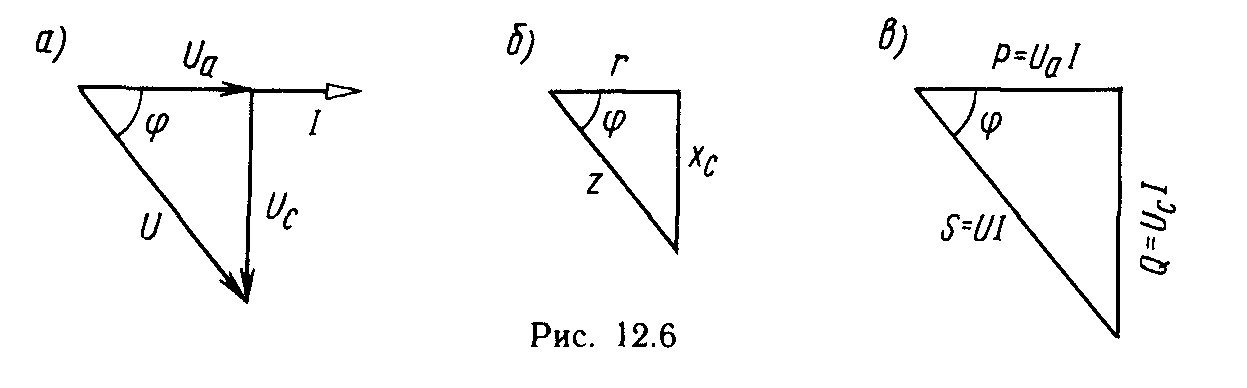
Из этого треугольника следует, что полное сопротивление рассматриваемой цепи

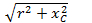                               (12.7)

Значит ток,

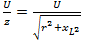                             (12.8)

Полученное выражение представляет собой закон Ома. При уве­личении сторон треугольника напряжений (рис. 12.6, а) в I раз получим подобный треугольник мощностей (рис. 12.6, в). Мощ­ности цепи:   активная  реактивная

, полная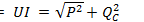

Разность фаз напряжений и тока в цепи можно определить из выражений:

 

§ 12.3. Цепь с активным сопротивлением, индуктивностью и емкостью

Если в неразветвленной цепи с активным сопротивлением r, индуктивностью L и емкостью C (hрис.12.7) протекает ток , то мгновенное значение приложенного к цепи напряжения . Напряжение на активном сопротивлении u_a совпадает по фазе с током в цепи i, напряжение на индуктивности u_L опережает ток на 90º, °, а напряжение на емкости и_с отстает от тока на 90°. Действую­щие значения напряжений на участках цепи: 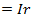, .Дейст­вующее значение напряжения на за­жимах цепи получим методом вектор­ного сложения: 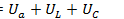. По­строим векторную диаграмму тока и напряжений. Сначала отло­жим вектор тока I (рис. 12.8,а). Вектор падения напряжения в активном сопротивлении U_aсовместим с вектором тока I, век­тор индуктивного падения U_Lотложим вверх под углом 90°, а вектор емкостного падения напряжения Uc— вниз под углом 90° к вектору тока I. Сложив векторы напряжений U_a, U_LиUc,получим вектор напряжения U,приложенного ко всей цепи. Векторная диаграмма построена для случая, когда x_L>x_cи цепь имеет активно-индуктивный характер. При этом условии U_L>Uc,а напряжение Uопережает по фазе ток I на угол ф. Если Xc>x_L,то U_c>U_Lи цепь имеет активно-емкостный харак­тер. При этом напряжение U(рис. 12.9) отстает по фазе от тока I на угол φ. При равенстве реактивных сопротивлений (x_L=xc) U_L=Uc(рис. 12.10).При этом напряжение Uсовпадает по фазе с током I (φ=0)и цепь носит активный характер. Этот режим в рассматриваемой цепи называется резонансом напря­жений.

 

 

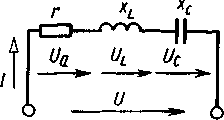
2.Треугольники сопротивлений и мощностей. Рассмотрим треугольник напряжений на рис. 12.8,а. Один катет этого треу­гольника выражает активное напряжение U_a,другой — реактив­ное напряжение цепи U_L— U_c,а гипотеза — полное напряжение U.Разделив стороны треугольника напряжений на ток I, полу­чим треугольник сопротивлений (см. рис. 12.8,6), из которого следует, что полное сопротивление цепи 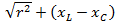². Поэтому ток в цепи

                                                  (12.9)

Если все стороны треугольника напряжений (см. рис. 12.8, а) умножить на ток I, то получим треугольник мощностей (см. рис. 12.8, в). Мощности: активная , где 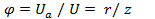; реактивная ; .

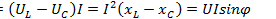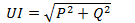Угол сдвига между напряжением и током равен углу между сторонами z и r треугольника сопротивлений иопределяется через тангенс:

или через косинус и синус

§ 12.4. Общий случай неразветвленной цепи

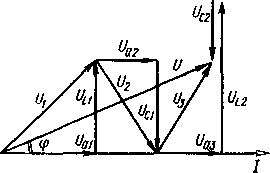
1.Векторная диаграмма тока и напряжений. На рис. 12.12 показана схема неразветвленной цепи, участки которой обла­дают активными и реактивными сопротивлениями. На векторной диаграмме (рис. 12.13, а) отложены векторы активных напряже­ний U_a1U_a2, и_аз, совпадающих по фазе с током, индуктивных — U_L1и UL2,опережающих ток по фазе на 90°, и емкостных — U_C1и U_C2, отстающих от тока по фазе на 90°. Сумма всех векто­ров напряжений равна вектору напряжения Uна зажимах цепи. На векторной диаграмме (рис. 12.14) векторы напряжений построены в той же последовательности, в которой соединены соот­ветствующие элементы цепи.

2.Треугольники сопротивлений и мощностей. Рассмотрим векторную диаграмму на рис. 12.13, а. Первый катет полученного треугольника напряжений равен арифметической сумме активных напряжений 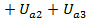, второй — алгебраической сумме реактивных напряжений , а гипотенуза — напряжению Uна зажимах цепи. Уменьшив все стороны этого треугольника в I раз, получим треугольник сопротивлений (рис. 12.13.б), из которого следует, что полное сопротивление цепи:

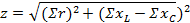
Таким образом, при последовательном соединении нескольких приемников складывать между собой можно только активные или только реактивные сопротивления, учитывая при этом их знаки. Индуктивные сопротивления берутся с положительным знаком, а емкостные - с отрицательным. Складывать модули полных сопротивлений нельзя. Для нахождения эквивалентного полного сопротивления цепи используется формула 12.10.Ток в цепи:

 

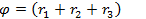Увеличив каждую из сторон треугольника напряжений в I раз, получим треугольник мощностей (рис. 12.13, в). Мощности цепи: активная , где  или 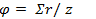;реактивная , где 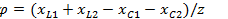; полная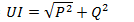

 

Рис. 12.14