1. Алгебраическая форма. Для расчета цепей переменного тока широко используются комплексные числа. Для этого изменяющиеся синусоидально ЭДС, напряжения и токи, а также сопротивления, проводимости и мощности изображаются комплексными числами. Это позволяет заменить графические действия над векторами алгебраическими действиями над комплексными числами, использовать для расчета цепей переменного тока законы Кирхгофа и все методы расчетов сложных цепей постоянного тока.
Из курса математики известно, что комплексное число можно представить в одной из трех форм: алгебраической, показательной и тригонометрической. В алгебраической форме комплексное число (сокращенно — комплекс) А выражается как сумма действительного числа А' и мнимого числа 
,т. е 
Мнимое число равно произведению мнимой единицы 
и коэффициента при ней А".
Для графического изображения комплексных чисел возьмем прямоугольную систему координат (комплексную плоскость, рис. 14.1) и условимся откладывать от горизонтальной оси действительные, или вещественные, числа, а по вертикальной — мнимые, принимая во внимание их знаки. Оси действительных и мнимых чисел сокращенно называют действительной и мнимой осями. Имея, например, комплекс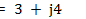 
, нанесем на действительную ось число 3, а на мнимую — мнимое число 
. Из концов полученных отрезков восставим перпендикуляры до их пересечения. Из начала координат в точку пересечения проведем вектор, который будет выражать заданное комплексное число. Таким образом, всякому комплексу на комплексной плоскости соответствует некоторый вектор. Число называют поворотным множителем. Умножение на jкомплексного числа приводит к повороту изображающего вектора на 90° в положительном направлении, т. е. против направления вращения часовой стрелки. Если задано действительно положительное число 
, то на комплексной плоскости оно изобразится отрезком или вектором, направленным по действительной положительной полуоси. При умножении числа на I получим мнимое число 
,которое изображают вектором, направленным по мнимой положительной полуоси,т. е. повернутым относительно первого вектора на 90° в положительном направлении.
2. Показательная форма. Для того чтобы комплексное число написать в показательной форме, необходимо знать его модуль и аргумент. Модуль комплексного числа определяется по теореме Пифагора: 
. Например, модуль комплекса 
(рис. 14.1) равен 
. Угол 
, составленный вектором с действительной положительной полуосью, называется аргументом комплекса.Положительные аргументы комплексов откладывают от действительной положительной полуоси против, а” отрицательные — по ходу часовой стрелки. Аргумент комплекса 
можно определить по тангенсу: 
. Например, для комплекса 
, откуда 
. Комплексное число в показательной форме выразится произведением модуля и поворотного множителя 
,где 
—основание натуральных логарифмов. Поворотный множитель 
показывает, что вектор на комплексной плоскости повернут относительно действительной положительной полуоси на угол а против направления движения часовой стрелки. Для рассмотренного примера 
Если аргумент комплекса отрицателен, то 
.
3. Тригонометрическая форма. При решении задач комплексным методом приходится переходить от показательной формы к алгебраической. Заданными являются модуль и аргумент комплекса, требуется определить действительную и мнимую части комплексного числа и представить его в алгебраической форме. Из прямоугольного треугольника (рис. 14.2) 
,а
. Следовательно, комплекс 
Полученная запись выражает тригонометрическую форму комплексного числа. Пусть задан комплекс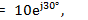 
а требуется записать этот же комплекс в тригонометрической и алгебраической формах. Для этого воспользуемся только что полученной формулой 
4. Сложение, вычитание, умножение и деление комплексных чисел. Над комплексными числами можно производить действия сложения, вычитания, умножения, деления. Для сложения и вычитания комплексы представляют в алгебраической форме. При сложении двух и нескольких комплексных чисел отдельно складывают их действительные и мнимые части 
. Пусть 
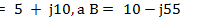. Тогда 
. При вычитании одного комплексного числа из другого вычитаются отдельно их действительные и мнимые части 
. Так как комплексное число можно представить вектором, то сложение или вычитание чисел соответствует сложению и вычитанию векторов. Умножение и деление комплексов производятся в показательной или алгебраической формах записи. В первом случае эти действия выполняются проще. Поэтому комплексы, заданные в алгебраической форме, для умножения или деления переводят в показательную. Произведение двух комплексов, выраженных в показательной форме, есть комплекс, модуль которого равен произведению модулей сомножителей, а аргумент — алгебраической сумме аргументов перемноженных комплексов: 
, где
, а 
. Пусть 
.Если сомножители имеют одинаковые модули, равные по величине, но противоположные по знаку аргументы, то их произведение равно квадрату модуля сомножителей: 
. Два таких комплекса называются сопряженными. Частное от деления двух комплексов, выраженных в показательной форме, есть комплекс, модуль которого равен частному от деления модуля комплекса делимого на модуль комплекса делителя, а аргумент равен алгебраической разности аргументов делимого и делителя: 
Пусть 
. Тогда 
