Основные понятия, относящиеся к переменным

ТОКАМ

§ 10.1. Период и частота переменного тока

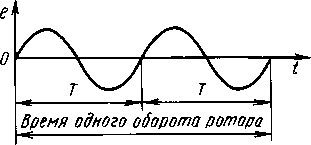
При передаче и распределении электрической энергии возни­кает необходимость в применении различных напряжений: высо­кого — для передачи энергии на большие расстояния и низко­го—для питания приемников энергии. Такое преобразование напряжений легко осуществляется лишь при переменном токе. Для этого используют электромагнитные аппараты — трансфор­маторы, имеющие простое устройство и высокий КПД. Современ­ная энергетика построена на использовании переменного тока, который получают на электрических станциях с помощью синх­ронных генераторов. Генераторы и двигатели переменного тока имеют высокие технико-экономические показатели, надежны в работе и удобны в эксплуатации. Электрическая энергия пере­менного тока широко используется в различных областях про­мышленности, сельского хозяйства, транспорта, связи и быта. В ряде отраслей техники используется энергия постоянного тока, для этого применяются выпрямители переменного тока, специаль­ные генераторы постоянного тока, а при небольшой мощности — первичные элементы и аккумуляторы. Наиболее распространен синусоидальный ток , график которого дан на рис. 10.1. По оси абсцисс отложено время t,а по оси ординат — ток i. Зна­чения тока, напряжения, ЭДС в любой данный момент време­ни называют мгновенными значениями и обозначают строчными буквами i, и, е, а наибольшие мгновенные значения периодически изменяющихся величин — амплитудными значениями и обозна­чают прописными буквами с индексом m: I_m, U_m, E_m.

Синусоидальный ток изменяется по значению и направлению. Одно его направление условно считают положительным, другое — отрицательным. Токи положительного направления откладывают выше оси абсцисс, а отрицательного — ниже. В начальный момент времени t_oток i =0 (рис. 10.1). Затем он увели­чивается, достигает максимального значения 1_т при t₁,уменьшается и при t₁снова становится равным нулю. После этого ток меняет направление, достигает отрицательного максимума, а затем вновь увеличивается до нуля. На этом заканчивается полный цикл изменений синусоидального переменного тока длительностью Т.

Время Т, в течение которого переменный ток совершает пол­ный цикл своих изменений, называется периодом переменного тока, а число периодов в секунду — его частотой:

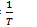                                    (10.1)

Единицей частоты в СИ служит герц (Гц). Частота равна 1 Гц, если полный цикл изменения тока совершается за 1 с. Бо­лее крупные единицы частоты — килогерц (кГц) и мегагерц (МГц): 1 кГц= 10³ Гц, 1 МГц = 10⁶ Гц. В СССР и Европе про­мышленной частотой является 50 Гц, в Америке, Канаде и Япо­нии — 60 Гц. Выбор промышленной частоты обусловлен технико­экономическими соображениями. При меньших частотах заметно мигание света осветительных приборов, а при больших — затруд­няется передача энергии на дальние расстояния. В различных отраслях техники кроме переменных токов промышленной часто­ты используют переменные токи других частот. Диапазон частот этих токов начинается с долей герц, достигает нескольких мил­лиардов герц. В радиотехнике, телевидении переменные токи вы­сокой частоты используют для передачи электрических сигналов без проводов посредством электромагнитных волн.

 

 

§ 10.2. Получение синусоидальной ЭДС

1. Устройство простейшего генератора переменного тока.

Принцип устройства генератора синусоидального тока поясняет рис. 10.2, а. На поверхности цилиндрического якоря I укреплен виток изолированного провода 2. Концы витка через щетки 3 и контактные кольца 4 соединены с приемником энергии r₁. Магнит­ная индукция поля, создаваемого неподвижной частью машины, распределяется по окружности якоря генератора по синусоидаль­ному закону. Это достигается особой формой полюсных наконеч­ников. У середины полюсов благодаря минимальному воздушно­му зазору магнитная индукция имеет максимальное значение В_т(рис. 10.2, б). От середины полюса к его краям воздушный зазор постепенно увеличивается, а магнитная индукция уменьшается.При этом векторы магнитной индукции в любой точке перпенди­кулярны поверхности якоря. В некоторых точках на поверхности якоря магнитная индукция равна нулю. Плоскость 0₁0₂ (рис. 10.2, б) называется нейтральной. Обозначим а угол между ней­тральной плоскостью 0₁0₂ и подвижным радиусом ОА. Тогда магнитная индукция в воздушном зазоре

.                                           (10.2)

 

 

 

2.Уравнения ЭДС, тока и напряжения. При вращении ротора (рис. 10.2, а) с постоянной скоростью vв проводниках витка аб и вг длиной l наводятся равные ЭДС .Так как проводники соединены последовательно и их ЭДС в контуре направлены одина­ково, то общая ЭДС витка .      Магнитная индукция

В в   воздушном зазоре изменяется синусоидально. Поэтому .В полученной формуле произведение 2B_mlvвыража­ет максимальное значение ЭДС Е_т в обмотке ротора при а= 90°. Поэтому

.                                             (10.3)

Таким образом, ЭДС генератора, как и его магнитная индук­ция, изменяется по синусоидальному закону. Ток в замкнутой це­пи

,

где r — эквивалентное сопротивление цепи.

Отношение  выражает максимальный ток I_т. Поэтому мгно­венное значение синусоидального тока

.                                               (10.4)

Зная мгновенное значение тока iи сопротивление приемника энергии r₁, можно определить мгновенное значение напряжения на зажимах генератора: . Так как I_тr₁ = U_т — максимальное значение напряжения, то .

3.Угловая скорость вращения ротора. Преобразуем формулу электродвижущей силы генератора переменного тока. За один оборот ротора при изменении угла а на 2л радиан происходит полный цикл изменений ЭДС продолжитель­ностью Т (рис 10.3). Поэтому угло­вая скорость вращения ротора ω=𝜶/ t =2𝛑/Т=2𝛑/T, а ЭДС двух­полюсного генератора

.(10.5)

 

Аналогично записывают уравнения синусоидального тока и напряжения:

                            (10.6)

.     (10.7)

 

4.Угловая частота. У генератора с одной парой полюсов (р = 1) одному обороту ротора соответствует один период Т элект­родвижущей силы. Если генератор имеет две пары полюсов (р = 2), то одному обороту ротора соответствуют два периода ЭДС (рис. 10.4). Таким образом, количество периодов синусои­дальной ЭДС, возникающей в витке за один оборот ротора, рав­но числу пар полюсов генератора (р). Произведение р𝜶 называ­ется электрическим углом, а отношение электрического угла ко времени — электрической угловой скоростью или угловой часто­той

                                   (10.8)

Угловая частота выражается в радианах в секунду (рад/с). При частоте f = 50 Гц ω = 314 рад/с. Частота ЭДС (или тока) у двухполюсного генератора (р = 1) равна числу оборотов ротора в секунду: f = n /60, где п — число оборотов ротора в минуту. У многополюсного генератора, имеющего р пар полюсов, частота

.                                             (10.9)

Для получения промышлен­ной частоты f =50 Гц ротор двухполюсного генератора дол­жен иметь частоту вращения 3000 об/мин, ротор четырех­полюсного генератора —

1500 об/мин, шестиполюсно­го — 1000 об/мин. Переменные токи высокой частоты получают с помощью электромашинных генераторов, а с более высо­кой частотой — с помощью специальных генераторов на элект­ронных лампах или полупроводниковых приборах.

§ 10.3. Действующее и среднее значения переменного тока

Действующее значение переменного тока. При расчетах и электрических измерениях широко применяется действующее значение переменного тока I. Для его определения можно исходить из теплового действия переменного тока в электриче­ской цепи. Действующее значение переменного тока равно значе­нию такого эквивалентного постоянного тока, который, проходя через то же сопротивление, что и переменный ток, выделяет в нем за период то же количество теплоты. На рис. 10.5 даны графики синусоидального тока i= I_msinω t и постоянного тока I (пунктирная прямая), которые выделяют одинаковое количество теплоты в некотором сопротивлении r за период Т. Количество теплоты, выделенное синусоидальным током iза элементарное время dt,d Q = i²rdt,а за время, равное                 периоду Т,

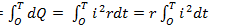                (10.10)

Такое же количество теп­лоты в сопротивлении r за время Т выделим постоян­ный ток I, равный действую­щему значению данного пере­менного тока:

.           (10.11)

Приравняв правые части (10.10) и (10.11) и решив полу­ченное равенство относительно тока I, получим

 

= =

Так как

,то

  (10.12)

Таким образом, действующее значение переменного синусои­дального тока меньше его амплитудного значения в √2 раз. Такое же соотношение справедливо для действующих значений синусоидального напряжения и ЭДС: и . Действующие значения обозначаются буквами без подстрочных индексов и указываются на шкалах электроизмерительных приборов (амперметров и вольтметров электромагнитной, электродинамической систем). Следовательно, если амперметр переменного тока показывает 10 А, а вольт­метр — 220 В, то максимальное значение тока в цепи , а максимальное значение напряжения .

2.Среднее значение переменного тока. При анализе работы различных выпрямителей, электрических машин и т.д. пользуются средними значениями изменяющихся величин:тока I _ср, напряжения U _ср, ЭДС Е_ср. Среднее арифметическое значение из всех мгновенных значений положительной полуволны называется с редним значением синусоидального тока за полупериод. Оно равно отношению количества электричества, кото­рое перемещается через поперечное сечение проводника за положительный полупериод, к продолжительности этого полупе риода. Таким образом,

Среднее за полупериод значение синусоидального напряжения U_ep= 0,637U_mи ЭДС E_Ср = 0,637E_m. За один период синусои­дальный ток дважды меняет направление. В течение первой поло­вины периода определенное количество электричества переме­щается по проводнику в одном направлении, а в течение второй это же количество электричества перемещается в обратном направлении. Следовательно, количество электричества, прошед­шее через поперечное сечение проводника, и среднее значение синусоидального тока за период равны нулю.

3.Коэффициенты формы и амплитуды. Отношение действую­щего значения переменного тока (напряжения или ЭДС) к сред­нему значению называется коэффициентом формы = k _ф= I / I _ср, а отношение амплитудного значения к действующему — коэффи­циентом амплитуды k_a — I_m/EДля синусоидального тока k _ф = = I / I _ср = 0,707 I _m/(0, 637 I_m) =1,11, ak_a= I_m / I = I_m /(0,707 I _m) = 1,41. Для кривых, имеющих более острую форму, чем синусои­да, и / k _ф>1,11 и k_a>1,41.

§ 10.4. Фаза. Разность фаз

1.Построение синусоидальной кривой. В §10.2 было выведе­но уравнение синусоидального тока:i= l_msin α=l_msinω t, где I_т — амплитудное значение тока; ω — угловая частота. В этом уравнении переменная величина ω t обозначает некоторый угол в радианах или градусах, который непрерывно возрастает пропорционально времени t.При увеличении угла cotменяется мгновенное значение тока I_т. Пусть амплитудное значение сину­соидального тока iI _m = 10 А. Определим мгновенные значения этого тока при следующих значениях угла ω t: 0, 30, 60, 90° и т. д. При ω t = 0 i = 10 sin0°, при ω t = 30° i= 10 sin30° = 5 А.

Аналогично определяют мгновенные значения тока при других значениях угла ωt. По результатам расчетов, сведенных в табл. 10.1, построен график данного синусоидального тока (рис. 10.8). Обратите внимание на то, что ток iдостигает значения 0, 5 I _т при угле 30°; 0,86 I_m — при угле 60°; I_m — при угле 90°.

1.  Начальная фаза синусоидальной величины. На рис. 10.8 начало координат совпадает с началом периода (синусоиды). Момент времени, в который синусоидальная величина (ток, напряжения, ЭДС) равна нулю и переходит от отрицательных значений к положительным, называется началом периода. Если в момент начала отсчета времени синусоидальный ток не равен нулю, то его уравнение принимает вид i= l_msin(ω t +Ψ). Аргу­мент синуса ω t +Ψ, выражаемый в радианах или градусах, называется фазным углом или фазой. Угол Ψ определяет смеще­ние синусоиды относительно начала координат и называется начальной фазой. Если t= 0, то i= I_msinΨ. Следовательно, начальная фаза — это электрический угол, определяющий сину­соидальный ток (напряжение или ЭДС) в начальный момент времени (при t = 0). Начальная фаза Ψ отсчитывается по оси ω t от начала синусоиды до начала координат. Поэтому при Ψ>0 начало синусоиды сдвинуто влево, а при Ψ<0 — вправо относительно начала координат. Общие выражения синусоидаль­ного напряжения и ЭДС имеют вид

Рис. 10.8

1.Угол и время сдвига фаз синусоидальных величин.

Нарис. 10.9 представлены графики синусоидального напряжения и тока с различными начальными фазами Ψ₁ и Ψ₂: , . Разность начальных фаз двух синусои­дальных величин одной частоты называется углом сдвига фаз.

В данном случае угол сдвига фаз напряжения и и тока i . Разделив угол сдвигафаз на угловую частоту, полу­чим время сдвига, на которое одна синусоидальная величина опережает другую: . При наличии угла сдвига фаз одна из сину­соидальных величин, у которой начало периода или положи­тельная амплитуда достигает­ся раньше, называется опе­режающей по фазе, а другая, у которой те же значения достигаются позже, — отстаю­щей по фазе. На рис. 10.9 напряжение и опережает по фазе ток i на угол φ. Синусоидальные величины одной частоты совпада­ют по фазе, если они имеют одинаковые начальные фазы. В этом случае угол сдвига фаз φ=0 и обе синусоиды достигают нулевых и положительных амплитудных значений одновременно. При угле сдвига фаз φ=±𝛑 синусоидальные величины одной частоты изменяются в противофазе.

§ 10.5. Векторная диаграмма

Расчет цепей переменного тока облегчается, если изображать синусоидально изменяющиеся токи, напряжения, ЭДС вращаю­щимися векторами. Пусть требуется изоб­разить вращающимся вектором синусои­дальный ток  Для этого возьмем прямоугольную систему коорди­нат хОу (рис. 10.10). Из начала координат О под углом Ψ проведем вектор I_m, длина которого в выбранном масштабе равна амплитудному значению тока I_т. Если вектор I_mвращать против движения часовой стрелки с угловой скоростью ω=2𝛑 f, то его проекция на ось ординат будет изменяться по синусоидальному закону. Предположим, что за время t

вектор повернется на угол ωt. Тогда проекция вектора на ось ординат . Значит, отрезок Оа соответст­вует мгновенному значению переменного тока, причем одному обороту вектора I_т будет соответствовать полный цикл измене­ний синусоидального тока.

Совокупность векторов, изображающих на одном чертеже несколько синусоидальных величин одной частоты, называется векторной диаграммой. Векторы, изображенные на такой диаг­рамме, имеют одинаковую угловую частоту ω. Поэтому их взаим­ное расположение на чертеже не меняется. Следовательно, при построении векторных диаграмм один вектор можно направить произвольно, а остальные расположить по отношению к первому под углами, равными соответствующим углам сдвига фаз, и оси координат не чертить. В большинстве случаев векторные диаг­раммы цепей переменного тока служат для определения соотно­шений между действующими значениями напряжений и токов. Поэтому диаграммы обычно строят не для амплитудных значе­ний, а для действующих, что обусловливает лишь уменьшение длины векторов в √2 раз.