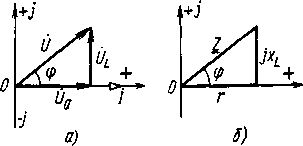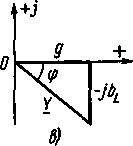1. Токи, напряжения в комплексной форме записи. Синусоидальные величины можно изображать комплексными числами. Комплексные значения тока, напряжения и.ЭДС принято обозначать прописными буквами с точкой: 
, а их модули, соответствующие действующим значениям, обозначают теми же буквами, но без точек над ними: 
. Вернемся к цепям с последовательным соединением активного сопротивления и индуктивности (см. § 12.1), активного сопротивления и емкости (см. § 12.2). Векторная диаграмма первой цепи, построенная на комплексной плоскости, дана на рис. 14.3, а, а второй — на рис. 14.4, а. В обоих случаях вектор тока 
направлен по оси действительных чисел вправо от начала координат. Поэтому комплекс тока 
/, где — модуль комплекса тока, а
|
Рис. 14.3 |
0° — его начальная фаза. Комплекс напряжения на зажимах цепи с последовательным соединением активного сопротивления и индуктивности (рис. 14,3,а) 
где Uaи 
— вещественная и мнимая части; Uи 
— модуль и начальная фаза комплекса напряжения. Таким образом, комплексное изображение синусоидальной величины определяет ее действующее (амплитудное) значение и начальную фазу. Пусть ток в катушке = 5 А, активное падение напряжения 
, а индуктивное 
. Тогда комплекс тока 
, а комплекс напряжения 
Для перехода от алгебраической формы к.показа тел ьной найд ем модуль комплекса напряжения:
. Значит 
. Поэтому комплекс напряжения 
|
|
2. Сопротивления и проводимости в комплексной форме.
Сопротивления и проводимости можно выразить комплексными числами. Комплексное сопротивление цепи обозначается 
,а комплексная проводимость— .При обозначении комплексных величин принято ставить точки только над теми комплексами, которые изображают синусоидально изменяющиеся величины. Поэтому для комплексов полного сопротивления и проводимости вместо точки над буквой ставят черту снизу. Модуль комплексного сопротивления цепи обозначают 
, а комплексной проводимости — . Рассмотрим треугольники сопротивлений и проводимостей цепей с последовательным соединениемактивного сопротивления и индуктивности (рис. 14.3,6, в), расположенные на комплексной плоскости. Активные сопротивления и проводимости изображены положительными отрезками на оси действительных чисел, а реактивные — положительными или отрицательными на оси мнимых чисел. С учетом этого составим комплексы полных сопротивлений и проводимостей. Для цепей с последовательным соединением и 
, а для цепей с и C 
. Модули и аргументы этих величин определяют по следующим формулам. Для цепей с последовательным соединением 
и 
и 
, а для цепей с и 
.
|
|
3. Комплексное значение мощности. В общем случае комплексное напряжение 
, а комплексное значение тока 
. Тогда сопряженный комплекс тока, отмеченный звездочкой 
для определения мощности в комплексной форме необходимо комплекс напряжения умножить на сопряженный комплекс тока: _ 
. Действительная часть полученного комплекса равна активной мощности, а мнимая — реактивной. Положительный знак перед мнимой частью полученного комплекса указывает на индуктивный характер нагрузки, а отрицательный — на емкостный.
§ 14.3. Законы Омы и Кирхгофа в комплексной форме
Закон Ома в комплексной форме 1=0/Z = 0Y.В этом выражении учитывается связь между действующими значениями напряжения Uи тока I,а также разность фаз между ними. Комплексное сопротивление ветви с сопротивлением г, индуктивностьюКомплексное эквивалентное
сопротивление неразветвленной цепи равно сумме всех ее комплексных сопротивлений: 
.Комплексная эквивалентная проводимосп при'параллельном соединении равна сумме комплексных проводимостей отдельных параллельных ветвей: 
. Комплексное сопротивление эквивалентное двум параллельным ветвям, 
. Первый закон Кирхгофа в комплексной форме записывают в виде 
, т. е. алгебраическая сумма комплексных токов, сходящихся в узле электрической цепи, равна нулю.
Для составления уравнения по первому закону Кирхгофа нужно выбрать условно положительные направления токов. Токи, направленные к узлу, записываются с положительным законом, а от узла — с отрицательным. Например, для узла А (рис. 14.5) получим 
. Второй закон Кирхгофа в применении к контуру цепи в комплексной форме записывается в виде = 
т. е. алгебраическая сумма действующих в контуре комплексных ЭДС равна алгебраической сумме комплексных падений напряжений. Уравнения по второму закону Кирхгофа записывают после выбора положительных направлений токов во всех ветвях цепи. Для схемы рис. 14.5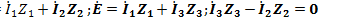 
|
|
§ 14.4. Расчет последовательно-параллельных цепей
Изображение синусоидальных величин комплексными числами позволяет применить для расчета цепей синусоидального тока те же методы и соотношения, которые использовались в цепях постоянного тока. Рассмотрим пример расчета цепи со смешанным соединением участков.
Глава 15
ТРЕХФАЗНЫЕ ЦЕПИ
