Поверхностный эффект и эффект близости

Постоянный ток распределяется по поперечному сечению про­водника равномерно, т. е. имеет одинаковую плотность во всех точках этого сечения. Сопротивление постоянному току вычисля­ют по формуле  Плотность переменного тока неодина­кова. Она возрастает от минимального значения на оси провода до максимального на его поверхности. Это явление называется поверхностным эффектом. Неравномерное распределение пере­менного тока в поперечном сечении проводника приводит к не­полному использованию этого сечения. Можно считать, что пере­менный ток проходит не по всему сечению проводника S, а толь­ко по его части S'.Так как S'<S,то сопротивление проводника переменному току больше сопротивления этого же проводника

постоянному току:

Поверхностный эффект возникает вследствие различной ин­дуктивности слоев проводника. Центральный слой проводника 1 (рис. 11.8) сцепляется с полным потоком Ф₍, а поверхностный слой 2 — только с внешним потоком Ф₂. Поэтому центральный слой по сравнению с поверхностным обладает большей индуктив­ностью и сопротивлением . Неравенство индуктивных сопротивлений различных слоев проводника вызывает неравно­мерное распределение переменного тока между этими слоями. В результате плотность переменного тока в проводнике возраста­ет от центра сечения к поверхности. Поверхностный эффект уси­ливается с ростом частоты, площади поперечного сечения прово­да, удельной электрической проводимости и магнитной проница­емости материала.

Рис. 11.8

При промышленной частоте влиянием поверхностного эффек­та часто пренебрегают. Исключение составляют медные и алюми­ниевые провода диаметром более 1 см и стальные любого сече­ния, имеющие большую магнитную проницаемость. На высоких частотах, используемых в радиотехнике, переменный ток прохо­дит по поверхностному слою проводника. Поэтому для экономии металла применяют полые провода (в виде трубок), снаружи по­крытые тонким слоем серебра, сни­жающим электрическое сопротивле­ние. В устройствах высокочастот­ной связи применяются биметалли­ческие провода, сердцевина которых выполнена из стали, а наружный слой, по которому проходит ток вы­сокой частоты, — из меди. Такие провода имеют высокую механиче­скую прочность и хорошую электро­проводность. На активное сопротив­ление влияет и эффект близости,заключающийся во взаимном влиянии нескольких близко лежа­щих проводов с переменными токами на распределение плот­ности тока по сечению. Если токи в двух параллельных проводах имеют одинаковое направление, то их плотность увеличивается в наиболее удаленных слоях. Если же токи направлены противо­положно, то их плотность увеличивается в наиболее близких слоях обоих проводов.

 

§ 11.4. Цепь с емкостью

1.Уравнения и графики тока и напряжения. Векторная диаг­рамма. На рис. 11.9 в электрическую цепь включен конденсатор емкостью С. Активное сопротивление и индуктивность конденса­тора настолько малы, что ими пренебрегают. Подведем к нему синусоидальное напряжение .Под действием напря­жения на пластинах конденсатора появится заряд

 

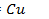.                                            (11.15)

 

За первую и третью четверти периода(рис. 11.10, а), когда напряжение и заряд увеличиваются, конден­сатор заряжается и в цепи возникает зарядный ток. За вторую и четвертую четверти периода, когда напряжение и заряд умень­шаются, конденсатор разряжается и в цепи возникает разрядный ток. Таким образом, при переменном напряжении конденсатор периодически заряжается и разряжается и в цепи проходит ток, равный скорости изменения заряда на пластинах конденсато­ра:

,                        (11.16)

где 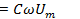                                          (11.17)

 

Векторная диаграмма цепи с емкостью дана Из (11.16) следует, что в цепи с емкостью ток опережает по фазе напряжение на 90°, Кривая тока показана на рис. 11.10, а. Здесь ток достигает максимума в те моменты времени, когда напряжение равно нулю. При максимальном напряжении токпрекращается. В первую и третью четверти периода конденсатор заряжается. При этом ток и напряжение имеют одинаковое на­правление (и знак). Во вторую и четвертую четверти периода конденсатор разряжается. При этом ток и напряжение имеют разные знаки. Ток достигает максимума при и = О, когда напря­жение изменяется с максимальной скоростью. При амплитудном значении напряжения скорость его изменения du/dt= 0 и ток

 

на рис. 11.10, 6.

2.Емкостное сопротивление. Преобразуем (11.17), разделив правую и левую части этого уравнения на , и получим

 или

 

Последнюю формулу можно написать и так:

                                        (11.18)

Формула (11.18) дает соотношение между током и напряже­нием и поэтому условно называется законом Ома для цепи с емкостью. Значение 1/(ωС) имеет размерность сопротивления (Ом) и называется реактивным сопротивлением емкости или емкостным сопротивлением (обозначается x _с). Таким образом,

                                        (11.19)

где С — емкость конденсатора, Ф; со — угловая частота, рад/с.

 

 

Если емкость конденсатора выразить в микрофарадах, то сопро­тивление

 

                                                (11.20)

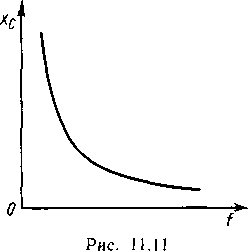
Для постоянного тока f = 0 и x_{c =∞}. Это значит, что при постоянном напряжении ток в цепи с емкостью равен нулю. С увеличением частоты (рис. 11.11) емкостное сопротивление уменьшается.

3.Мгновенная и реактивная мощности. В цепи с емкостью ток опережает по фазе напряжение на 90°. Поэтому, когда ток дости­гает максимума, напряжение равно нулю (см. рис. 11.10, а). И наобо­рот, при максимальном напряжении в цепи ток исчезает. При выбранном начале отсчета времени, в начале и конце каждой четверти периода ток или напряжение, а значит, и мгновенная мощность 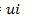равна нулю. В промежутках между этими моментами мощность положительна или отрицательна. В первую и тре­тью четверти периода, когда ток и напряжение имеют одинаковые зна­ки, мгновенная мощность положительна. В эти промежутки времени конденсатор заряжается и потребляемая им энергия накапливается в электрическом поле конденсатора. Во вторую и четвертую четверти периода, когда ток и напряжение имеют разные знаки, мгновенная мощность цепи отрицательна. В это время конденсатор разряжается, т. е. запасенная в его электри­ческом поле энергия возвращается генератору. Таким образом, в цепи происходит периодический обмен энергией между генера­тором и конденсатором. Выведем уравнение мгновенной мощ­ности. Синусоидальное напряжение изменяется по уравнению

а ток . Мгновенная мощность

Следовательно, мгновенная мощность изменяется по синусои­дальному закону с двойной частотой. Амплитудное значение такой мощности равно UI,а среднее значение за период — нулю. Амплитудное значение мощности в цепи с емкостью называется реактивной мощностью .Она характеризует скорость обмена энергией между генератором и цепью с емкостью

Глава 12