Цепь с параллельным соединением катушки и конденсатора

1. Векторная диаграмма напряжения и токов. Рассмотрим разветвленную цепь переменного тока, в одну из ветвей которой включена емкость. В первую параллельную ветвь (рис. 13.3), как и в предыдущем случае, включим активное и индуктивное x сопротивления, а во вторую — активное и емкостное сопротивления. К цепи подведем синусоидальное напряжение, действующее значение которого равно U.Ток в первой ветви

а во второй —

Зная, что ток отстает по фазе от напряжения Uна угол , а ток опережает это же напряжение на угол , строим векторную диаграмму (рис. 13.4,а). По горизонтальной оси отложим вектор напряжения U.Вектор тока повернем относительно вектора напряжения по часовой стрелке на угол , а вектор тока — против часовой стрелки на угол . Начало вектора совместим с концом вектора Тогда замыкающий вектор I будет выражать ток в неразветвленной части цепи.

Расчет токов. Из векторной диаграммы видно, что векторы токов ₂ и I образуют треугольник. Поэтому арифметическая сумма токов и больше тока I. Ток в неразветвленной части ценеразветвленной части цепи . Разложим все токи на активную и реактивную составляющие. Активные составляющие токов и направлены в одну сторону — по направлению вектора напряжения, а реактивные — в противоположные. Реактивная составляющая первого тока отстает по фазе от напряжения на 90°, а второго опережает это же напряжение на 90°, т. е. реактивные составляющие токов в параллельных ветвях находятся в противофазе (сдвинуты между собой по фазе на 180°). Поэтому активная составляющая тока цепи , а реактивная . Ток в неразветвленной части цепи .

5) Зг

2. Применение метода проводимости. Если все стороны многоугольника токов уменьшить в Uраз, то получим многоугольник проводимостей (рис. 13.4,6). Проводимости параллельных ветвей: активные и . реактивные и полные и .Проводимости всей цепи: активная ,реактивная , полная Обратим внимание на то, что реактивная проводимость всей цепи находится как разность реактивных проводимостей параллельных ветвей. Для определения токов необходимо соответствующие проводимости умножить на напряжение источника энергии:

, ; . (13.6)

Векторная диаграмма и многоугольник проводимостей на рис. 13.4,а,б построены для случая, когда . Здесь ток цепи I отстает по фазе от напряжения на угол и вся цепь имеет активно-индуктивный характер. Когда же (), вся цепь имеет активно-емкостный характер. При этом ток цепи режает напряжение на угол . Возможен режим, при котором Реактивные токи полностью компенсируют друг друга, и ток в неразветвленной части цепи совпадает по фазе с напряжением. При этих условиях в цепи возникает резонанс токов. Этот режим работы электрической цепи подробно рассмотрен в § 13.4.

§ 13.3. Общий случай цепи с параллельными ветвями

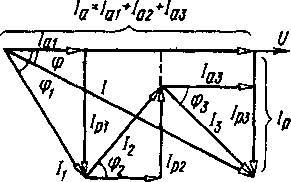
1. Векторная диаграмма напряжения и токов. Цепь, изображенная на рис. 13.5, состоит из трех параллельных ветвей. Первая ветвь для источника питания является активно-индуктивной нагрузкой, а вторая — активно-емкостной. Поэтому ток отстает по фазе от напряжения Uна угол а ток опережает это напряжение на угол . Характер третьей ветви зависит от соотношения ее индуктивного и емкостного сопротивлений. Допустим, что , тогда третья ветвь имеет активно-индуктивный

Рис. 13.5 Рис. 13.6

характер и ток отстает по фазе от напряжения на угол . С учетом этого построена векторная диаграмма рассматриваемой цепи (рис. 13.6). Для упрощения диаграммы начало вектора тока совмещено с концом вектора тока ,а начало вектора тока — с концом вектора тока . При таком построении замыкающий вектор выражает ток Iв неразветвленной части цепи.

2. Расчет токов. Из векторной диаграммы видно, что активная составляющая тока цепи равна арифметической сумме активных составляющих токов в ветвях: , а реактивная — алгебраической сумме реактивных составляющих: В ветвях в r и Lреактивные составляющие токов считаются положительными, а в ветвях с r и C — отрицательными. Ток цепи , а токи в параллельных ветвях

Резонанс токов

1. Векторная диаграмма напряжения и токов. Резонансная частота. Вернемся к параллельному соединению катушки индуктивности и конденсатора (см. рис. 13.3). В § 13.2 указывалось, что в цепи при равенстве составляющих токов возникает резонанс токов. На рис. 13.8 приведена диаграмма цепи при резонансе токов. Активные составляющие токов в параллельных ветвях и совпадают по фазе с приложенным напряжением U,а реактивные , сдвинутые на 180°, полностью компенсируют друг друга. Поэтому общий ток цепи 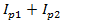. При этом угол сдвига фаз общего тока цепи и напряжения равен нулю. Так как ,то при резонансе

или . (13.7)

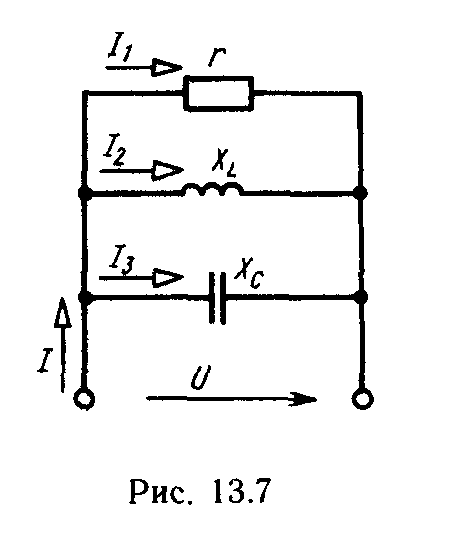
Следовательно, при резонансе токов реактивная проводимость катушки индуктивности равна реактивной проводимости конденсатора . Значит, реактивная проводимость всей цепи

Если это уравнение решить относительно частоты, то получим

(13.8)

Из (13.8) видно, что резонансная частота зависит не только от индуктивности Lи емкости С, но и от активных сопротивлений контура и . В частном случае, когда активные сопротивления малы и ими можно пренебречь, частота резонанса токов , т. е. совпадает с частотой резонанса напряжений. Такое же равенство частот возникает при равенстве активных сопротивлений

2. Особенности резонанса токов. Полная проводимость всей цепи с параллельным соединением катушки и конденсатора

. (13.9)

ная проводимость становится наименьшей из всех возможных при изменении частоты источника . Наоборот, сопротивление всей цепи становится наибольшим. При максимальном сопротивлении общий ток в цепи 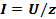становится наименьшим. Он совпадает по фазе с напряжением источника ( =0). Характер изменения полного сопротивления и тока всей цепи от частоты показан на рис. 13.9. При резонансе токи в параллельных ветвях и могут быть значительно больше общего тока цепиmI. Это объясняется тем, что реактивные составляющие токов катушки индуктивности и конденсатора взаимно уравновешиваются и поэтому не влияют на ток . Выясним зависимость общего тока цепи при резонансе от активных сопротивлений контура 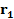и . С уменьшением этих сопротивлений уменьшаются активные мощности и . В результате снижаются активные составляющие токов 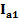|, и ток в .Для идеального контура, когда

Если это уравнение решить относительно частоты, то получим

(13.8)

3. Особенности резонанса токов. Полная проводимость всей цепи с параллельным соединением катушки и конденсатора

. (13.9)

l,z“

При резонансе b₁и b₂,а y=g₁+g₂т.е полная проводимость равна активной проводимости цепи. Обратим внимание на то,что полная проводимость становится наименьшей из всех возможных при изменении частоты источника f.

Наоборот, сопротивление всей цепи становится наибольшим. При максимальном сопротивлении общий ток в цепи становится наименьшим. Он совпадает по фазе с напряжением источника ( =0). Характер изменения полного сопротивления и тока всей цепи от частоты показан на рис. 13.9. При резонансе токи в параллельных ветвях и могут быть значительно больше общего тока цепиmI. Это объясняется тем, что реактивные составляющие токов катушки индуктивности и конденсатора взаимно уравновешиваются и поэтому не влияют на ток . Выясним зависимость общего тока цепи при резонансе от активных сопротивлений контура и . С уменьшением этих сопротивлений уменьшаются активные мощности и . В результате снижаются активные составляющие токов , и ток в . Для идеального контура, когда , токи и . В этом случае между катушкой индуктивности и конденсатором происходит обмен энергией без активных потерь. Сопротивление идеального контура 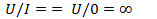, т. е. становится бесконечно большим. В действительности любой колебательный контур имеет активные сопротивления. Поэтому 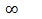и . Чем меньше активные сопротивления контура, тем больше его сопротивление и тем меньший ток проходит в цепи от источника энергии к контуру. При резонансе реактивные мощности Поэтому реактивная мощность всей цепи . От источника питания к контуру поступает только активная энергия. Резонанс токов широко используется в радиотехнических цепях (устройствах автоматики, телемеханики и связи). Использование резонанса токов позволяет улучшить коэффициент мощности электрических установок промышленных предприятий.

Коэффициент мощности

1. Определение и расчет коэффициента мощности. При активной нагрузке, к которой можно отнести лампы накаливания, нагревательные приборы, ток и напряжение совпадают по фазе ( = 0). При этом активная мощность 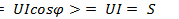, т. е. равна полной мощности. В цепях с активным сопротивлением и индуктивностью или с активным сопротивлением и емкостью угол сдвига фаз напряжения и тока 0, а активная мощность меньше полной: 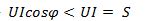.Электрическая энергия, израсходованная в цепи переменного тока за время t,называется активной.

При неизменной активности мощности Р активная энергия

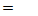Pt.Произведение реактивной мощности Qи времени tназывается реактивной энергией ,а отношение активной мощности приемника энергии к полной — коэффициентом мощности:

- (13.10)

В общем случае активная мощность меньше полной, поэтому 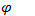<1. И только при активной нагрузке, когда вся мощность является активной , . У большинства приемников меняется во время их работы. Например, 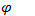асинхронного электродвигателя изменяется от 0,2 до 0,85 при увеличении его механической мощности от нуля до номинальной. При этих условия работу установки характеризует средневзвешенный коэффициент мощности. Его находят за определенный промежуток времени (например, за месяц) по показаниям счетчиков активной и реактивной энергии:

(13.11)

2. Значение коэффициента мощности. Для выяснения значения коэффициента мощности обратимся к основным характеристикам питающего генератора: номинальному напряжению току и мощности . Пусть = 1200 В, = 200 А. Тогда . К генератору поочередно присоединим приемники с таким же номинальным напряжением и током, но с различным . При подключении активной нагрузки, когда 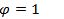, активная мощность генератора , т. е. равна полной мощности. Если теперь к тому же генератору подключить нагрузку, имеющую = 0,5, то активная мощность генератора , т. е. снизится в два раза. Несмотря на это, по обмоткам генератора и соединительным проводам проходит тот же ток (200 А). Значит, генератор работает с полной номинальной мощностью и подключать к нему дополнительную нагрузку нельзя. Активная мощность генератора уменьшилась за счет увеличения его реактивной мощности, бесполезно загружающей генератор и линию электропередачи. Если к генератору подключить нагрузку с 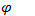= 0, то его активная мощность . Итак, один и тот же генератор при номинальной полной мощности может отдавать приемникам энергии различную активную мощность. С уменьшением приемника активная мощность генератора уменьшается, а реактивная увеличивается. Наилучшее использование номинальной мощности генератора возможно при его работе с номинальными напряжением и током, =1. В этом случае генератор может развивать наибольшую мощность, равную полной номинальной мощности: .Это возможно, если все подключенные к генератору приемники будут работать при =1. Однако 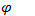= 1 только при активной нагрузке. При активно-индуктивной нагрузке 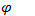<l. В этом случае применяют ряд мер, повышающих установки до значений, близких к единице (0,95-=- 1).

3. Способы улучшения коэффициента мощности. Расчет емкости статистических конденсаторов. Различают естественные и искусственные способы улучшения коэффициента мощности. Известно, что электродвигатели переменного тока, трансформаторы работают с наибольшим при полной их загрузке. Поэтому электродвигатели и трансформаторы нужно выбирать по требуемой мощности, не допуская их недогрузки и работы вхолостую. Способы повышения коэффициента мощности, связанные с правильным выбором оборудования и его эксплуатацией, называются естественными. Во многих случаях естественные способы улучшения дополняют искусственными, при которых применяют специальное оборудование.

При одном из них параллельно приемнику подключают статические конденсаторы так называемой компенсационной установки (рис. 13.10).

Векторная диаграмма такой установки показана на рис. 13.11. Вектор напряжения Uотложен в горизонтальном направлении. Ток приемника отстает от напряжения на угол , а ток конденсатора опережает это же напряжение на угол 90°. Общий ток цепи равен геометрической сумме и . Реактивная составляющая тока приемника частично (или полностью) компенсируется током конденсатора .

В связи с этим уменьшаются общий ток цепи с до и угол сдвига фаз с до . Активная составляющая тока приемника I_па не меняется. На рис. 13.12,а,б показаны треугольники мощностей установки до и после включения конденсаторов. Реактивную мощность установки выразим через неизменную активную мощность Р. До подключения конденсатора .а после включения . Реактивная мощность статических конденсаторов .Эту же мощность выразим через напряжение сети Uи проводимость конденсатора .Следовательно,

. Отсюда емкость батареи конденсаторов

При полной компенсации, когда = 0,

Однако для полной компенсации реактивной составляющей тока нагрузки требуется значительная емкость конденсаторов, что в ряде случаев экономически невыгодно.

Глава 14