Собственные колебания в контуре

1. Колебательный контур. В цепи с последовательным соеди­нением активного сопротивления, индуктивности и емкости мож­но получить резонанс напряжений. Для понимания этого явления очень важно иметь представление о процессах, происходя­щих в колебательном контуре. Колебательный контур (рис. 12.15) состоит из катушки индуктивности Lи конденсатора С. В поло­жении 1 переключателя П конденсатор С подключается к источ­нику с постоянным напряжением Uи заряжается от него до амплитудного напряжения U_m= U.В процессе заряда в электри­ческом поле конденсатора накапливается потенциальная электри­ческая энергия .После того как конденсатор пол­ностью зарядится, переключатель П поставим в положение 2. При этом конденсатор отсоединяется от источника и начинает разряжаться на катушку индуктивности. При разряде напряже­ние и энергия электрического поля конденсатора снижаются до нуля.

Разрядный ток конденсатора в катушке индуктивности наво­дит ЭДС самоиндукции, которая противодействует любому изме­нению тока в цепи. Благодаря этому разрядный ток конденса­тора изменяется плавно, без скачков. К моменту, когда конден­сатор разрядится полностью и напряжение на его пластинах будет равным нулю, ток в катушке индуктивности достигнет амплитудного значения I_т. При этом в магнитном поле катушки сконцентрируется максимальное количество энергии . Если не учитывать активное сопротивление контура, на котором электрическая энергия преобразуется в тепловую, то можно

считать, что энергия электрического поля конденсатора полностью преобразуется в энергию магнитного поля катушки ин­дуктивности:

                                  

                                  (12.12)

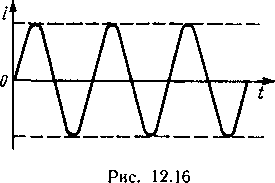
Достигнув максимального значения, ток и энергия магнитного поля начнут уменьшаться. ЭДС самоиндукции при этих условиях направлена в сторону убывающего тока и поддерживает его. При уменьшении тока происходит заряд конденсатора, в результате которо­го увеличивается напряжение на его пластинах. Энергия магнитного по­ля переходит в энергию электри­ческого поля. К тому моменту, когда ток в цепи станет равным нулю, напряжение на конденсаторе вновь достигает амплитудного значения U_m.При этом энергия магнитного поля катушки индук­тивности полностью преобразуется в энергию электрического поля конденсатора. После этого процесс разряда и заряда кон­денсатора повторяется. Изменяется лишь направление тока в контуре. Таким образом, между катушкой индуктивности и конденсатором происходит обмен энергией. При этом в колеба­тельном контуре возникает переменный синусоидальный ток определенной частоты (рис. 12.16). Такие колебания тока (и напряжения) в контуре называют незатухающими собственными колебаниями.

2.Частота незатухающих собственных колебаний. Выведем формулу частоты незатухающих собственных колебаний контура (ω₀ и fo).Амплитудное значение тока в катушке индуктивности

Отсюда угловая частота незатухающих собственных колебаний ω₀= 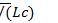а частота                  

                          (12.13)

Следовательно, частота собственных колебаний зависит от индуктивности и емкости контура, причем с увеличением индук­тивности и емкости частота незатухающих собственных колеба­ний уменьшается. Из (12.12) вытекает также важное соотноше­ние:

 

Значение имеет размерность сопротивления; оно называется характеристическимили волно­вымсопротивлением колебательного контура.

 

Затухающие колебания в контуре. В реальном колебатель­ном контуре всегда имеется некоторое активное сопротивление r. Поэтому энергия контура превращается в теплоту. Значит, каж­дое очередное колебание в контуре будет совершаться с меньшим запасом энергии. Значит каждое очередное колебание в контуре будет совершаться с меньшим запасом энергии. В результате амплитуда собствен­ных колебаний будет уменьшать­ся (рис. 12.17) и они через некоторое время прекратятся. Частота затухающих колебаний, несмотря на изменение амплиту­ды, остается неизменной. Она за­висит от индуктивности, емкости и активного сопротивления контура:

 

§ 12.6. Резонанс напряжений

1. Условия получения резонанса напряжений. Резонанс на­пряжений возникает в цепи, состоящей из активного сопротив­ления, индуктивности и емкости (см. рис. 12.7), при равенстве ее реактивных сопротивлений x_L = x_c.Так как ,а

то при резонансе . Отсюда частота колебаний

По этой же формуле опре­деляется и частота незатухающих собственных колебаний конту­ра f ₀ (см. § 12.5). Следовательно, при резонансе напряжений частота подводимого к контуру переменного напряжения совпа­дает с частотой собственных колебаний контура, т. е. f= fo.Ре­зонанс напряжений можно получить при постоянных параметрах контура, изменяя частоту подводимого напряжения. Если частота источника энергии остается постоянной, то для получения резонанса изменяют индуктивность катушки Lили емкость кон­денсатора С.

2.Особенности резонанса напря­жений. Полное сопротивление при резонансе , т. e. равно активному сопро­тивлению (рис. 12.18, б). Оно стано­вится наименьшим из всех возмож­ных при изменении частоты источ­ника f.Это значит, что индуктивное и емкостное напряжение взаимно уравновешиваются и полное напря­жение источника равно активному напряжению цепи U_a(рис. 12.18, а). Под действием напряжения цепи при минимальном сопротивлении в цепи возникает наиболь­ший ток /= U/z= U/г. При этом он совпадает по фазе с напря­жением цепи, угол φ становится равным нулю. При малом активном сопротивлении цепи напряжения на индуктивности и емкости могут быть значительно больше напряжения источника. Действительно, ток в цепи , а напряжения .При резонансе каждое из реак­тивных сопротивлений равно волновому сопротивлению цепи:

. Величина Q= р/r назы­вается добротностью контура(цепи). Отсюда . Следовательно, при резонансе напряжения U_Lи U_cбольше напряжения Uна зажимах цепи в Qраз. При равенстве реак­тивных сопротивлений x_L = х_сравны и реактивные мощности. Поэтому реактивная мощность цепи . Это зна­чит, что при резонансе напряжений между индуктивностью и емкостью происходит полный обмен энергиями. Энергия магнит­ного поля катушки переходит в энергию электрического поля конденсатора и наоборот. Источник переменного напряжения не участвует в обмене и доставляет энергию лишь активному сопротивлению цепи r.

1. 3.Практическое значение резонанса напряжений. Резонанс напряжений используется для настройки приемных и передаю­щих устройств в области автоматики и связи на определенную частоту. На рис. 12.19 показан так называемый входной фильтр локомотивнойсигнализации. По рельсам проходит импульсный ток частотой f. Он индуцирует в приемных катушках ЭДС этой же частоты. Так как катушки вместе с конденсатором С и пер­вичной обмоткой трансформатора w ₁ образуют контур, настроен­ный на частоту f, то в нем возникает резонанс напряжений. Ток в контуре становится максимальным, и на вто­ричной обмотке трансформатора w₁возникает максимальное напряже­ние частотой f, передаваемое на уси­литель и далее к соответствующей аппаратуре. Для частот, отличаю­щихся от частоты f, контур имеет большое сопротивление. Поэтому ток и напряжение этих частот на выходе трансформатора ничтожно малы. Таким образом, входная цепь локомотивной сигнализации являет­ся фильтром, который пропускает к аппаратуре только токи одной частоты и защищает ее от токов других частот.

Резонанс напряжений широко используется в радиотехнике. Например, для мощного излучения антенный контур передающих радиостанций всегда настраивают в резонанс колебаниям, соз­даваемым генератором. В электроэнергетических устройствах резонанс напряжений применяется редко. Высокие напряжения на индуктивности и емкости при резонансе, значительно превы­шающие напряжение на зажимах цепи, представляют опасность для изоляции и обслуживающего персонала.

§ 12.7. Резонансные кривые

1.Зависимость сопротивления от частоты. Пусть цепь, сос­тоящая из последовательно соединенных активного сопротивле­ния r, индуктивности Lи емкости С, находится по переменным синусоидальным напряжением U,частоту которого можно плавно изменять от нуля до максимума. При изменении частоты будут изменяться сопротивления x_L, х_с, r, ток I, напряжения U_a, U_Lи U_C,мощности Р, Q, Sи угол сдвига фаз φ между напряжением и током. Кривые зависимости I, U_L, U_cи φ от частоты называют резонансными кривыми.Построим кривые изменения сопротивле­ния x_L, х_си z(рис. 12.20,а). Индуктивное сопротивление прямо пропорционально частоте (на графике — прямая линия). При = 0,при . Емкостное сопро­тивление х_с— обратно пропорционально частоте (на графи­ке — гипербола). При . а при . Полное сопротивление цепи

.

При резонансной часто­те x_L— x_c.Поэтому реактивное сопротивление х= xl— Хс — 0, а полное сопротивление z = rстановится минимальным. Если частота fисточника больше резонансной f о, то x_L>x_cи в цепи кроме активного возникает дополнительное сопротивление

Отсюда полное сопротивле­ние цепи становится больше активного сопротивления. При f= ∞ xl =∞ и 2=∞. При частотах, меньших резо­нансной, в цепи также появляется сопротивление .По­этому полное сопротивление цепи так­же становится больше активного соп­ротивления. При f =О x_С= ∞ и z=∞. Таким образом, полное сопротивление цепи с увеличением частоты (начиная с f = 0) уменьшается, при резонанс­ной частоте /о становится минималь­ным, а затем снова увеличивается до ∞.

1. Резонансные кривые. Ток в цепи (рис. 12.20, б) увеличивается от нуля при f=О, когда 2=∞, до наибольшего при резонанс­ной частоте f ₀, а затем уменьшается до нуля при f=∞. Угол сдвига фаз напряжения и тока φ также зависит от частоты источника питания. При резо­нансной частоте f о напряжение и ток совпадают по фазе, цепь имеет актив­ный характер и угол φ=0. При увели­чении частоты от f о До ∞ угол ср уве­личивается от 0 до 90°, а цепь носит индуктивный характер.

Если частоту источника питания уменьшать от foдо 0, то угол φ будет изменяться от 0 до 90°. Таким образом, при увеличении частоты от 0 до ∞ угол ср увеличивается от -90° до 0 при резо­нансной частоте, а затем до +90°. При этом цепь сначала имеет емкостный, затем активный и, наконец, индуктивный характер. Индуктивное напряжение (рис. 12.20, в). При увеличении частоты от 0 до f ₀ ток I и сопротивление x_Lувели­чиваются. Поэтому увеличивается и индуктивное напряжение, равное произведению этих величин. Можно показать, что при дальнейшем увеличении частоты индуктивное напряжение увели­чивается, достигает наибольшего значения U_Lmaxпри частоте f_L,а затем плавно уменьшается до напряжения источника U. Напряжение на емкости U_c = Ixcпри f =0 равно напряжению на зажимах цепи U(все напряжение сосредоточивается на бесконечно большом сопротивлении х_с). С увеличением частоты емкостное напряжение увеличивается; при частоте f_cдостигает максимального значения Ucmах = Ulmax, а затем уменьшается до нуля (при f= 0, х_с = 0 и Uc= 0).

При резонансной частоте f ₀ напряжения на индуктивности и емкости .Качество резонансного контура определяется добротностью Q.Чем больше добротность контура, тем ближе расположены частоты f_Lи f _с к резонансной частоте f о и тем острее характеристики I, U_Lи Uc-Вблизи резонансной частоты f_aможно выделить область частот, в пределах которой ток в контуре не меньше 0,707 резонансного значения. Эту область частот называют полосой пропускания контура. Ширина полосы пропускания зависит от добротности контура. Чем больше добротность контура, тем уже резонансная кривая тока и меньше полоса пропускания. Резонансными кривыми называют также зависимости тех же величин от изменяющейся емкости С или индуктивности L при постоянной частоте f ( или ω)

 

Глава 13

РАЗВЕТВЛЕННЫЕ ЦЕПИ ПЕРЕМЕННОГО ТОКА

§ 13.1. Цепь с двумя параллельно соединенными катушками индуктивности

1. Векторная диаграмма напряжения и токов. Параллельное соединение приемников (двигателей, осветительных устройств, бытовых приборов) находит самое широкое применение. Все приемники при этом включаются в общую сеть переменного тока с определенным напряжением U.Рассмотрим цепь с параллель­ным соединением двух катушек индуктивности (рис. 13.1). Каждую катушку можно рассматривать как обмотку электро­двигателя переменного тока. Первая параллельная ветвь содержит активное сопротивление  и индуктивность первой катушки, а вто­рая — активное сопротивление  и ин­дуктивность второй катушки. Цепь с последовательным соединением активного сопротивления и индуктивности рассмот­рена в § 12.1. Ток первой катушки hотстает по фазе от напряжения Uна угол  (см. рис. 12.2, а). Величину этого угла можно определить по сопро­тивлениям  и (см. рис. 12.2, б): Ток второй катушки I₂ отстает по фазе от напряжения Uна угол , откуда . Построим векторную диаграмму цепи с параллель­ным соединением катушек индуктивности (рис. 13.2, а). За исходный вектор диаграммы примем вектор напряжения U, одинаковый для обеих катушек. По отношению к этому вектору под углами  и  в сторону отставания строим векторы и . Начало вектора  совместим с концом вектора .Тогда замыкающий вектор Iбудет выражать ток внеразветвленной части цепи.

Рнс. 13.1

2.Расчет токов и мощностей. Токи в параллельных ветвях определим по закону Ома ;

Значительно сложнее определить ток , равный геометрической сумме токов и . Векторы токов  и  образуют треугольник, каждая сторона которого меньше суммы двух других его сторон. Поэтому ток всей цепи меньше арифметической суммы токов в параллельных ветвях. Для определения тока в неразветвленной части цепи каждый из токов  и  разложим на две взаимно перпендикулярныесостав­ляющие:активную, совпадающую по фазе с напряжением U,и реактивную, отстающую от напряжения на 90° (рис. 13.2,а). Активная составляющая первого тока а второго . Реактивная составляющая токов  и равны .  Сложивактивные составляющие то­ков и , получим активную составляющую тока всей цепи , а при сложении реактивных составляющих — реактивную составляющую тока . Ток всей цепи оп­ределим по теореме Пифагора:

 

в)

 

(13.1)

Следовательно, для нахождения тока всей цепи нужно снача­ла определить активные и реактивные составляющие токов в параллельных ветвях, затем активную и реактивную составляю­щие тока всей цепи. Активная мощность цепи ,а реактивная .Полная мощность a

2. Метод проводимостей. Обратимся к рис. 13.2,а. Токи и их составляющие образуют много­угольник токов. Если все его стороны уменьшить в Uраз, то по­лучим многоугольник проводимостей (рис. 13.2,6). На эквива­лентной схеме каждую катушку можно изобразить двумя па­раллельно соединенными элементами: проводимостями активной gи реактивной b (рис. 13.2,в). Проводимости первой ветви: активная

,(13.2) реактивная

(13.3) полная

                                     (13.4)

Проводимости второй ветви: активная ; реактивная ; полная . Из многоугольника прово­димостейвидно, чтоактивная проводимость цепи ,ареактивная                                .

Полная проводимостьвсей цепи Таким образом, проводимость параллельных ветвей и всей цепи можно определить через активные и реактивные сопротивления катушек индуктивности. Токи катушек  и I в неразветвленной части цепи прямо пропорциональны соответст­вующим проводимостям и напряжению U:

;. .                         (13.5)

Рассмотренный метод расчета разветвленных цепей перемен­ного тока называется методом проводимостей.По проводимости можно определить также мощности цепи и . Мощности: активная реактивная ;полная