Сложение и вычитание синусоидальных величин

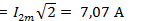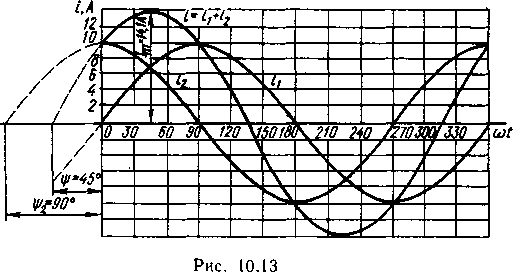
1. Сложение и вычитание синусоидальных величин на времен- ной диаграмме. При расчете электрических цепей переменного тока приходится складывать и вычитать синусоидальные токи, напряжения или ЭДС. Рассмотрим следующий числовой пример. Пусть два приемника энергии соединены параллельно. Ток перво­го , а второго . Действующие значения этих токов:  и . Требуется написать уравнение тока iв неразветвленной части цепи и вычислить его действующее значение. По первому закону Кирхгофа, 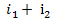. Мгновенные значения токов i ₁, i₂и iзависят от электрического угла ωt.При ωt= 0, i₁ = 10 sin0° = 0°, i ₂ = = 10 sin90° =10 A, i = i₁ +i₂=0+10= 10 А.

При ω = 30° h= 10 sin30° = 5 А, i ₂ = 10 sin120° = 8,6 A, i = = 5 + 8,6= 13,6 А. Аналогично определяют токи 0, i ₂и i₂при дру­гих значениях угла ωt.По мгновенным значениям (табл. 10.2) построены графики токов i, i ₂ и i ₁ (рис. 10.13). Из графиков видно, что ток i, как и токи i₁и i ₂, изменяется по синусоидальному закону с той же частотой.

2.Сложение и вычитание синусоидальных величин на вектор­ной диаграмме. Рассмотрим, как осуществляется сложение тех же синусоидальных токов i ₁ и i ₂ на векторной диаграмме (рис. 10.15). Ток i ₂ опережает по фазе ток i ₁, на 90°. Поэтому вектор I_2m повернут относительно вектора i_1m на 90° против движения часовой стрелки. Сложив по правилу параллелограмма векторы l_1mи I_2m, получим вектор I_т, изображающий общий синусоидальный ток. Его максимальное значение

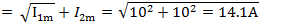, а тангенс начального фазового угла

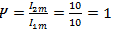1.

Значит, ф=45°. Такой же результат был получен при сложении токов на временной диаграмме. Однако на векторной диаграмме операции сложения выполняются проще. Таким образом, на векторной диаграмме производится сложение векторов, изображающих амплитудные (или действующие) зна­чения синусоидальных величин (токов, напряжений или ЭДС).

Если нужно сложить не два, а большее число синусоидальных токов, то удобно пользоваться правилом многоугольника. По это­му правилу векторы переносятся параллельно самим себе так, чтобы начало второго вектора совпадало с концом первого, начало третьего — с концом второго и т. д. (рис. 10.17). Затем изначала первого вектора в конец последнего проводят замыкаю­щий вектор, изображающий суммарный синусоидальный ток. Для того чтобы из одного вектора вычесть другой, необходимо к первому прибавить второй, но взятый с обратным знаком. Изменение знака вектора означает поворот его на ±180°. На рис. 10.18 векторы I₂ и — I₂— равны по абсолютной величине, но сдвинуты на угол 180°. Геометрическая сумма векторов I₁и — I₂ выразится новым вектором:

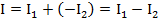
Приведенныеположения о геометрическом сложении и вычитании векторов синусоидальных токов одной частоты справедливы и для других синусоидально изменяющихся величин (напряжений и ЭДС).

Глава 11