Метод эквивалентного преобразования треугольника и звезды сопротивлений

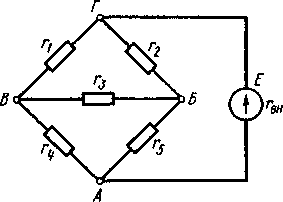
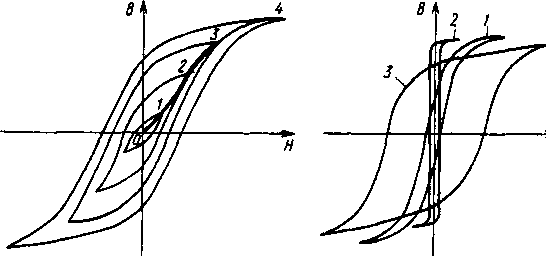На рис. 6.10, а дана электрическая цепь с одним источником питания, широко применяемая в области электрических измере­ний. Особенностью этой цепи является наличие в ней соединений, называемых треугольником и звездой. Треугольником сопротив­лений называют соединение трех ветвей, образующих замкнутый контур с тремя узлами. В схеме рис. 6.10, а имеется два треуголь­ника c сопротивлениями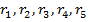

Звездой сопротивлений называют соединение трех ветвей, имеющих общий узел. На рис. 6.10, а звезду сопротивлений обра­зуют ветви с сопротивлениями 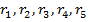. Любой тре­угольник сопротивлений можно заменить эквивалентной звездой. В результате замены получается другая схема, позволяющая упростить расчет. Например, схема рис. 6.10, а после замены треугольника сопротивлений  эквивалентной звездой 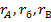 в упрощается (рис. 6.10, б) и содержит только последовательно и параллельно соединенные участки.

 

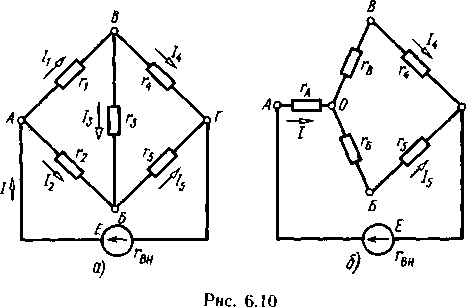
Эквивалентность треугольника и звезды сопротивлений за­ключается в том, что их замена не изменяет потенциалов узловых точек (на схеме рис. 6.10, а точек А, Б, В), являющихся вершинами треугольника и эквивалентной звезды. Не изменяются также токи, напряжения и мощности в остальной части схемы, не затронутой преобразованием. Для перехода от треугольника соп­ротивлений к эквивалентной звезде пользуются следующими фор­мулами:

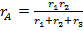; ; (6.11)

.

Сопротивление  луча А равно произведению двух сопротив­лений треугольника, сходящихся в узле A, деленному на сумму всех сопротивлений треугольника. Так же определяются сопротивления 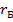 и . Вернемся к схе­ме рис. 6.10,6. Ее легко рассчи­тать и определить токи I, I₄ и I₅, которые не изменились после замены треугольника эквивалент­ной звездой. Остальные токи I₁, I₂ и I₃Находят из уравнений по законам Кирхгофа, составленных для исходной электрической схе­мы цепи (рис. 6.10,а).

В некоторых электрических цепях расчет упрощается после замены трехлучевой звезды сопротивлений эквивалентным треугольником. При преобразовании звезды в эквивалентный треугольник пользуются следующими формулами:

 

 

 

 

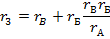
Таким образом, сопротивление стороны эквивалентного треугольника равно сумме сопротивления двух лучей звезды, присоединенных к те же вершинам, что и сторона треугольника,и их произведения, деленного на сопротивление третьего луча звезды.

 

 

Четырехполюсники

Основные уравнения четырехполюсника. Четырехполюсни­ком называют электрическую цепь, имеющую два входных и два выходных зажима. К входным зажимам 1—1' присоединяется ис­точник электрической энергии, а к выходным 2—2' — приемник с сопротивлением r_н (рис. 6.12). Таким образом, четырехполюсник является промежуточным звеном между источником энергии и ее приемником. К четырехполюсникам можно отнести линии передачи энергии и сигналов, несущих информацию, трансформаторы, рель­совые цепи, фильтры, предназначенные для разделения сигналов, и другие электрические устройства. Внутренняя электрическая схема четырехполюсников может быть весьма сложной и содер­жать ветви с источником энергии. Четырехполюсники с источника­ми энергии называют активными, а без источников — пассивными.

 

 Любой пассивный линейный четырехполюсник можно заменить эквивалентным с тремя сопротивлениями, соединенными звездой (Т-образная схема замещения) или треугольником (П-образная схема замещения). На рис. 6.13 показана Т-образная схема заме­щения пассивного четырехполюсника. Напряжение и ток на входе четырехполюсника обозначают U₁, I₁, а на выходе четырехполюс­ника U₂, I₂. Для Т-образной схемы замещения выразим U₁, I₁ через U₂, I₂. Входной ток /, 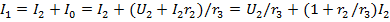. Входное напряжение

После введения обозначений  , , ,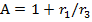

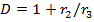
получим основные уравне­ния четырехполюсника: 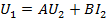, 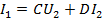. Значе­ния А, В, С, D называются коэффициентами четырехполюсника и связаны между собой соотношением . Справедли­вость этого равенства легко доказать, подставляя вместо А, В, С, D их выражения через сопротивления . Коэффициенты четырехполюсника А и D — отвлеченные числа, В имеет размер­ность сопротивления, С — размерность проводимости. При работе четырехполюсника в качестве промежуточного звена между источ­ником и приемником энергии его внутренняя схема и значения ее сопротивлений не меняются. Поэтому коэффициенты А, В, С, D являются постоянными, т. е. не зависят от сопротивления нагрузки r_н или напряжения U₁ источника энергии.

При заданном режиме работы приемника (напряжении U₂ и то­ке I₂), пользуясь основными уравнениями, легко определить на­пряжение U₁ и ток I₁ на входе четырехполюсника. Все расчеты с сопротивлениями внутренней схемы четырехполюсника при этом исключаются. Таким образом, расчет сложной электрической цепи можно упростить, если в ней выделить четырехполюсник. Разли­чают симметричные и несимметричные четырехполюсники. Четы­рехполюсник называется симметричным, если при перемене места­ми источника энергии и приемника значения входных и выходных напряжений и токов не меняются. В симметричном четырехполюс­нике A = D и А² -ВС = 1.

2.Экспериментальное определение коэффициентов четырехпо­люсника. Коэффициенты А, В, С, D четырехполюсника находят из опытов холостого хода и короткого замыкания. В опыте холостого хода (рис. 6.14) вторичные зажимы разомкнуты и I₂ = 0. Обозна­чив входное напряжение U_1xx, входной ток I_1ХХ, выходное напряже­ние U_2хх, перепишем основные уравнения четырехполюсника для холостого хода: U_1xx, = A/ U_2хх и, С= I_1ХХ / U_2хх. Отсюда А = U_1xx / U_2хх, С= I_1ХХ/ U_2хх. В опыте короткого замыкания (рис. 6.15) выходные зажимы 2—2' замкнуты через очень малое сопротивление ампер­метра, а к входным зажимам подведено пониженное напряжение U_1кз такое, чтобы выходной ток I_2кз не превышал номинального значения. Основные уравнения четырехполюсника в условиях ко­роткого замыкания (U₂= 0) примут вид U_1кз = B/I_2кз и I_1кз=DI_2кз

Отсюда B=U_1кз/I_2кз,D= I_1кз/ I_2кз

3.Режим четырехполюсника при нагрузке. Пусть заданы на­пряжение U₂ и ток I₂ на нагрузке. При проведении опыта холостого хода четырехполюсника напряжение на выходных зажимах 2—2’ можно выбрать равным заданному напряжению U₂, а при проведе­нии опыта короткого замыкания в выходном контуре установить ток I₂Заданные величины U₂ и I₂ устанавливаются регулировкой напряжения на входе четырехполюсника. Тогда напряжение и ток на входе четырехполюсника будут равны при холостом ходе U_1xx =A U₂, I_1ХХ = С/ U₂; при коротком замыкании U_1к = BI_2кз, I_1кз = D/I_2кзпри заданном режиме U₁ = A U₂ + BI₂ = U_1xx+ U_1кз, I₁ = C U₂  +DI₂ = I_1ХХ + I_1кз Следовательно, при любом заданном режиме (U₂, I₂) работы приемника напряжение U₁ и ток I₁ можно определить путем наложения соответствующих режимов холостого

 

 

Глава 7 МАГНИТНОЕ ПОЛЕ § 7.1. Основные понятия

1. Определение и основные свойства магнитного поля.

В проводнике с током и вокруг него возникает магнитное поле При достаточно сильном токе его можно обнаружить с помощью магнитной стрелки (рис 7.1, а) Если к про­воднику с электрическим током (на рис. 7.1, б этот проводник обозначен кружком с крести­ком, так как ток направлен за плоскость чертежа) поднести магнитную стрелку, то она изменит свое положение. После отключения тока магнитная стрелка возвратится в исход­ное положение Магнитное поле возникает не только вокруг проводников с током, но и при движении любых электрически заряженных час­тиц и тел, а также при изменении электрическо­го поля В постоянных магнитах оно создается и вращений их вокруг своих осей.

Магнитное поле имеет ряд физических свойств. Основным свойством является силовое воздействие его как на движу­щиеся в нем заряженные тела, так и на неподвижные проводники с электри­ческим током. Магнитное поле может также намагничивать ферромагнитные тела, возбуждать ЭДС в проводниках, которые перемещаются в магнитном поле. Эти свойства имеют большое практическое значение. Силовое дейст­вие магнитного поля используется в электродвигателях, многих электроиз­мерительных приборах, электротехни­ческих аппаратах. На использовании индуцированных ЭДС осно­ван принцип действия генераторов, трансформаторов, различных преобразователей и других устройств.

 

                                                                                                 рис7.2.

 

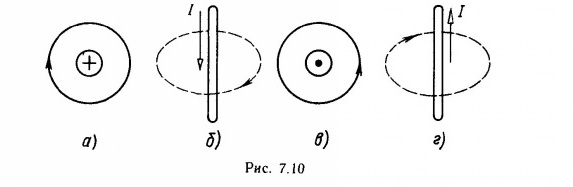
2. Направление магнитного поля. За направление магнитного поля в заданной точке принимается такое, которое укажет север­ный конец магнитной стрелки, помещенной в эту точку. Для того чтобы наглядно графически изобразить магнитное поле, введено понятие о магнитных линиях. Их проводят так, чтобы направле­ние касательной в каждой ее точке совпало с направлением поля. Направление магнитных линий вокруг прямолинейного проводни­ка с током определяется по правилу буравчика: если поступа­тельное движение буравчика совпадает с направлением тока в проводе, то вращение рукоятки буравчика укажет направление магнитных силовых линий.

На рис. 7.2 ток I направлен за плоскость чертежа. Для того чтобы буравчик двигался в этом направлении, его следует вра­щать по ходу часовой стрелки. Значит, магнитные линии распо­ложены по концентрическим окружностям и направлены по ходу часовой стрелки. Направление магнитного поля в каждой точке совпадает с касательной, проведенной к магнитной линии. На рис. 7.3 показаны магнитные линии поля витка с током, а на рис. 7.4 — катушки с током. Для этого случая правило буравчи­ка имеет другую формулировку: если рукоятку буравчика вра­щать по направлению тока в витках, то его поступательное дви­жение совпадает с направлением магнитных линий внутри ка­тушки.Направление поля внутри катушки можно определить и по правилу правой руки: если ладонь правой руки положить на вит­ки катушки так, чтобы четыре сложенных вместе пальца показы­вали направление тока в витках, то отогнутый под прямым углом большой палец укажет направление поля внутри катушки.

 

§7.2. Величины, характеризующие магнитное поле

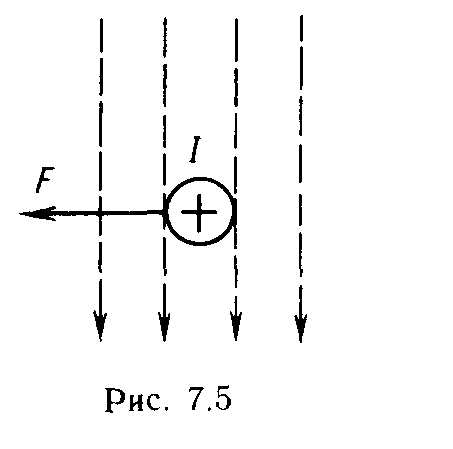
1. Магнитная индукция. Интенсивность магнитного поля в каждой его точке определяется магнитной индукцией, обозначае­мой В. Для того чтобы дать определение магнитной индукции и установить ее единицу в СИ, воспользуемся силовым воздействи­ем магнитного поля на проводник с током. В однородном поле (рис. 7.5), магнитная индукция которого постоянна и равна В, помещен прямолинейный проводник длиной / с током /. Причем угол между проводником и магнитными линиями равен 90°. По закону Ампера, установленному опытным путем, известно, что на такой проводник действует электромагнитная сила

BIl.

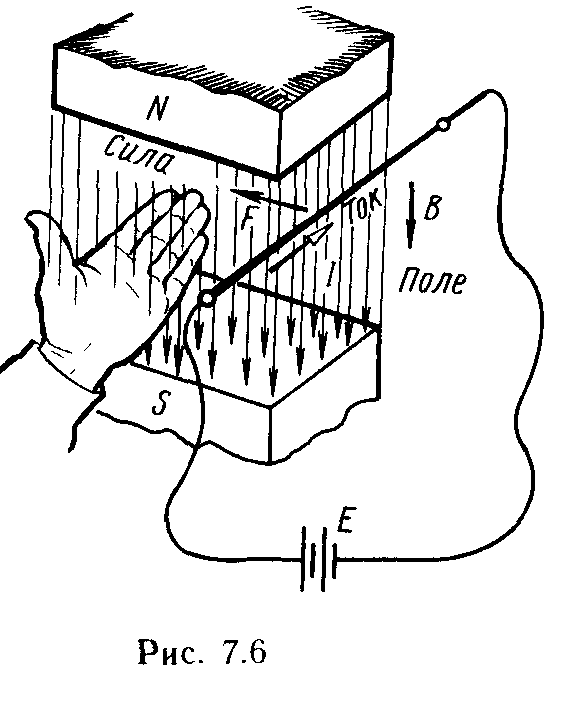
Направление электромагнитной силы определяется по прави­лу левой руки: если ладонь левой руки расположить так, чтобы магнитные линии входили в нее, а четыре выпрямленных пальца совпадали с направлением тока, то отогнутый под прямым углом большой палец укажет направление силы (рис. 7.6).

Из формулы (7.1) магнитная индукция

 

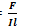(7.2)

 

Если 1=1 А, /=1 м, то B=F.Отсюда следует оп­ределение магнитной индукции: магнитная индукция есть величина, численно равная силе, которая действует на проводник длиной 1 м с током 1 А, помещен­ный в однородное магнитное поле перпендикулярно его направле­нию. Из (7.2) определим единицу магнитной индукции в СИ:

[В] = H/(А·м) = Дж/(м·А·м) = В·А·с/(А·м²) = В·с/м².

 

 

Для В·с установлено наименование — вебер (Вб). Следова­тельно, единицей индукции служит Вб/м². Ее называют тесла [Тл]. Магнитную индукцию иногда выражают и в более мелких единицах — гауссах: 1 Гс= 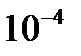 Тл. Магнитная индукция — величина векторная. Направление вектора индукции в каждой точке совпадает с направлением поля.

 

Магнитное поле считается однородным, если векторы В магнитных индукций во всех его точках одинаковы. В противном случае поле считается неодно­родным. С помощью магнитных линий можно не только указать направление магнитного поля, но и выразить значение магнитной индукции. Неоднородное магнитное поле будет изображаться зам­кнутыми линиями, проведенными с неодинаковой плотностью.

 

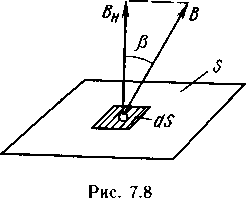
2. Магнитный поток. На рис. 7.7 перпендикулярно вектору магнитной индукции В однородного поля расположена площадка 5. Произведение магнитной индукции В однородного поля и пло­щадки 5, перпендикулярной вектору этой индукции, называется магнитным потоком:

.                                                   (7.3)

Для определения магнитного потока в неоднородном поле по­ступают следующим образом. На заданной поверхности Sвыде­ляют элементарную площадь dS(рис. 7.8). Находят нормальную составляющую вектора магнитной индукции на элементарной площадке: В, где 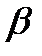 — угол между нормалью к площадке dSи вектором магнитной индукции В. Затем находят элементар­ный магнитный поток через элементарную площадь dS:dФ= dS. Магнитный поток через всю поверхность Ф =

Ф= 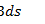. Выведем размерность магнитного потока в СИ: [ф] = [BS] =  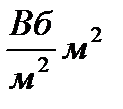= Вб. Более мелкой единицей является максвелл (Мкс): 1 Вб = 10⁸ Мкс.

3.Абсолютная и относительная магнитная проницаемости. Напряженность магнитного поля.

 

Интенсивность магнитного поля зависит от среды (вещества), в которой Она возникает.Это можно объяснить следую­щим образом. Движение электронов по орби­там внутриатома рассматривается как элементарный ток. При отсутствии внешнего магнитного поля элементарные токи внутривещества ориентированы беспорядочно и Рис. 7.9 магнитное поле этих токов не обнаруживается. Под действием внешнего поля, в которое вносится вещество, появляется согласованная ориен­тацияэлементарных токов и они создают свое дополнительноемагнитноеполе,                                  налагаемое на внешнее и изменяющее его.Таким образом, любое вещество, находящееся в магнитном поле внешних токов, приходит в состояние намагниченности, которое характеризуется возникновением в нем добавочного магнитного поля.

Интенсивность и характер намагниченности различных ве­ществ в одинаковом магнитном поле внешних токов значительно отличаются. Поэтому все вещества можно разделить на три груп­пы: диамагнитные (вода, водород, кварц, серебро, медь и т.д.), в которых магнитное поле элементарных токов направлено про­тив поля внешних токов, т. е. результирующее поле ослабляется; парамагнитные (алюминий, кислород, воздух и т.д.); ферромаг­нитные (железо, никель, кобальт и некоторые сплавы).

Парамагнитные и ферромагнитные вещества характеризуются тем, что магнитное поле элементарных токов в них направлено одинаково с полем внешних токов. В результате магнитное поле усиливается. Однако намагниченность ферромагнитных веществ в отличие от парамагнитных во много раз сильнее при одинако­вом магнитном поле внешних токов.

Магнитные свойства веществ характеризуются абсолютной магнитной проницаемостью 𝝁̥₀ Абсолютную магнитную проницае­мость пустоты называют магнитной постоянной:        

𝝁̥₀=4𝛑·10⁻⁷ Гн/м. Генри — единица индуктивности (Гн = Ом • с). От­ношение абсолютной магнитной проницаемости данного вещества 𝝁̥ₐ к магнитной постоянной 𝝁̥₀ называется относительной магнитной проницаемостью т.е.

Ясно, что для пустоты 𝝁ᵣ=1. Относительная магнитная проницаемость парамагнитных веществ больше единицы, а диа­магнитных — меньше единицы.Это различие большинства ве­ществ незначительно. Например, у парамагнитного алюминия 𝝁ᵣ=1,000023, а у диамагнитной ме­ди 𝝁ᵣ=0,99991. Поэтому при тех­нических расчетах магнитная про­ницаемость диамагнитных и пара­магнитных материалов и сред принимается равной единице.

В электротехнике особое значение имеют ферромагнитные материалы, относительная магнитная проницаемость которых до­стигает десятков тысяч и зависит от магнитных свойств матери­ала, температуры, напряженности магнитного поля. Большая магнитная проницаемость ферромагнетиков используется для того, чтобы усиливать магнитные поля и придать им нужную кон­фигурацию в электрических машинах и аппаратах.

При расчетах магнитных цепей необходимо применять величи­ну, которая, так же как и магнитная индукция, характеризует магнитное поле, но в то же время не зависит от свойств среды. Такой величиной является напряженность магнитного поля Н. Напряженность магнитного поля и магнитная индукция связаны простым соотношением

 

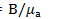                                    (7.4)

Напряжен напряженность магнитного поля — векторная величина. На­правление вектора напряженности Н в изотропных средах, т. е. в средах с одинаковыми во всех направлениях магнитными свойствами, совпадает с направлением поля в каждой его точке. Напряженность магнитного поля в СИ выражается в амперах на метр (А/м):

[В] = [В/𝝁ₐ] = Вб • м/ [Н] =[В/𝝁ₐ]Вб·м/(м² • Гн) = В • с • м/(м²• Ом·с) = А/м.

 

 

 

 

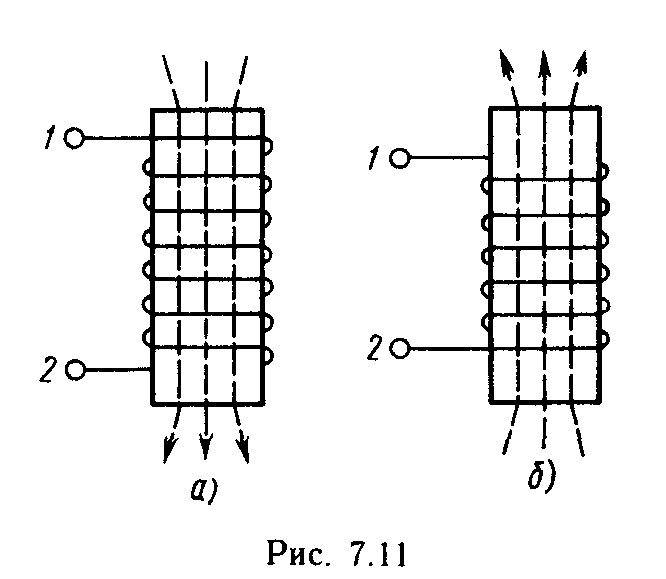
Единицей напряженности является также эрстед (Э): 1 Э = 80 А/м = 0,8 А/см.

Закон полного тока

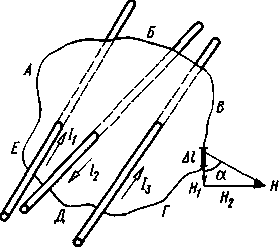
Магнитное поле и электрический ток неразрывно связаны друг с другом. Значит, напряженность, индукция и поток зависят от тока. Зависимость между напряженностью магнитного поля и током можно установить, применив закон полного тока. На рис. 7.12 показаны три проводника с электрическим током. Вокруг проводников проведен контур АБВГДЕА. В разных точках этого контура напряженность магнитного поля будет различной по зна­чению и направлению. Предположим, что на бесконечно малом элементе длины контура ∆ l вектор напряженности поля образует с элементом длины ∆l угол α. В этом случае вектор Н можно разложить на две составляющие: 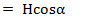 и 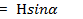. Про­дольная составляющая напряженности магнитного поля ∆l на­правлена по длине ∆ l, а поперечная H— под углом 90° к ∆l. Произведение 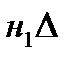l называется магнитным напряжениемAU_Mна участке , которое будет поло­жительным, если вектор Hiсов­падает с направлением обхода контура, например с движением часовой стрелки. Магнитное нап­ряжение выражается в амперах [U_M]=[ 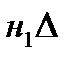l ] = А.

Сумму элементарных магнит­ных напряжений вдоль замкнуто­го контура называют цир­куляцией вектора напряженности магнитного поля по замкнутомуконтуру. Алгебраическая сумма токов, пронизывающих по­верхность, ограниченную контуром, называется полным током ∑l

Закон полного тока формулируется следующим образом: цир­куляция вектора напряженности магнитного поля по замкнутому контуру равна полному току, пронизывающему поверхность,ограниченную этим контуром.

Токи, пронизы­вающие поверхность, считаются положительными, если их маг­нитное поле совпадает с положительным направлением обхода контура. Так, на рис. 7.12 при обходе контура по часовой стрелке токи I₁ и I₃ положительные, а ток I₂отрицательный.

 

 

 

                                                                                    Рис 7.12.

 

§ 7.4. Магнитное поле тока р прямолинейном проводе

1. Магнитное поле за пределами провода. Рассмотрим магнит­ное поле тока I в прямолинейном проводе большой длины (рис. 7.13). Напряженность и магнитную индукцию такого поля легко определить по закону полного тока. Выведем формулу напряжен­ности магнитного поля в точке А, которая удалена от оси прово­да на расстояние х>R

(R — радиус провода). Для этого в плос­кости, перпендикулярной оси проводника, проведем окружность радиусом х с центром на оси провода. Так как все точки этой окружности удалены от оси провода на одинаковое расстояние, то напряженность поля в них одинакова.

Вектор напряженности в любой точке контура направлен по касательной к силовой линии._ Поэтому продольная составляю­щая напряженности поля Hi = H.Площадь, ограниченную выде­ленным контуром, в данном случае пронизывает только один токI. Значит, 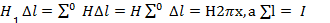. На осно­вании закона полного тока приравниваем правые части этих уравнений, т. е.Н2𝛑х = I. Отсюда

 

Значит, напряженностьи индукция магнитного поля прямо пропорциональны току и обратно пропорциональны рас­стоянию от оси провода. Можно пользо­ваться (7.5) и (7.6) в том случае, если x>R, а длина провода значительно боль­ше расстояния х.

2.Магнитное поле внутри провода. Определим напряженность поля внутри провода, т. е. в точках, удаленных от оси провода на расстояние х<R

 

 

 

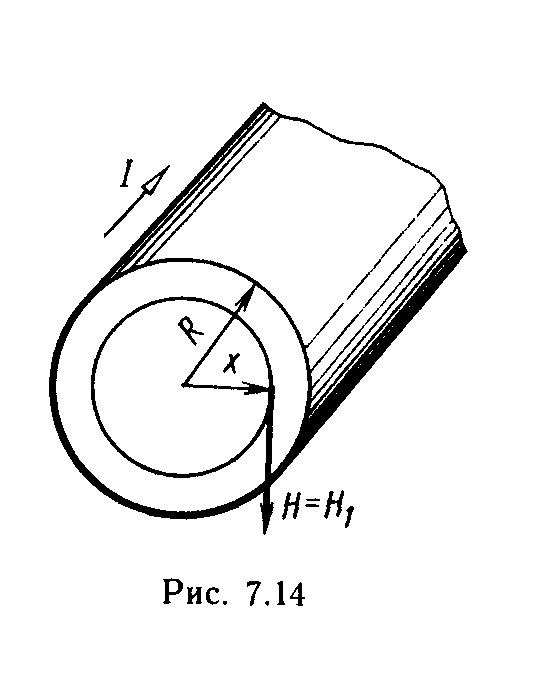
Для этого из центра про­вода проведем окружность радиусом х.

Площадь, ограниченная этой окруж­ностью, пронизывается током

I = 𝛿Sx, здесь 𝛿 = I/(𝛑R²) — плотность тока в проводе; Sx=𝛑x²— площадь, ограни­ченная выделенным контуром. Следо­вательно,

I_x = I𝛑x²/(nR²) = Ix²/R².Так как напряженность поля Н в силу симметрии во всех точках выделенного контура постоянна, то, по закону полного тока,

Отсюда

 

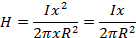
Следовательно, напряженность и индукция в любой точке внутри провода прямо пропорциональны расстоянию х этой точки от оси провода. В частности, на оси провода, т. е. при х = О, напряженность

Н= 0 и В = 0. От оси провода к его поверхности напряженность и магнитная индукция линейно возрастают, до­стигая наибольшего значения на его поверхности.

 

 

2. Магнитное поле нескольких проводов с токами. В некото­рых случаях магнитное поле создается системой проводов с электрическими токами. Находят магнитную индукцию в какой- либо точке этого поля следующим образом: а) определяют значе­ние и направление магнитной индукции B1 в данной точке от тока первого проводника; б) определяют значение и направление маг­нитных индукций В2, Вз и т. д. в этой же точке от других токов; в) путем сложения векторов магнитных индукций B1, В2, Вз... и т. д. находят искомый вектор магнитной индукции В.

 

 

 

 

 

 

 

§ 7.5. Магнитное поле кольцевой и прямой катушек

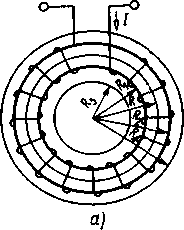
1. Магнитное поле кольцевой катушки. Воспользуемся зако­ном полного тока для определения напряженности магнитного поля кольцевой катушки с током I, имеющей wравномерно распределенных витков (рис. 7.19, а). Для этого выделим замк­нутый контур по средней магнитной линии радиуса R.Во всех точках этого контура вектор напряженности магнитного поля совпадает с касательной к контуру и имеет одинаковое значение. Поэтому 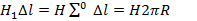а полный ток,пронизывающий ограниченную контуром поверхность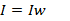

По закону полного тока .,т.е

Следова­тельно, напряженность поля катушки по средней магнитной линии                            

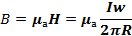
а магнитная индукция

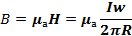
' рис 7.19

 

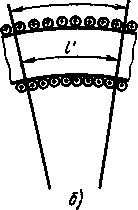
2. Магнитное поле прямой катушки. Напряженность магнит­ного поля кольцевой катушки численно равна отношению намаг­ничивающей силы Iwко всей длине окружности 2𝛑R.Напряжен­ность поля находят и другим способом: путем деления намагничи­вающей силы Iw'части дуги окружности на длину этой дуги I' (рис. 7.19, б), т. е. 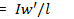'.Прямую катушку (рис. 7.20) можно рассматривать как часть кольцевой с бесконечно большим радиу­сом. Поэтому напряженность магнитного поля по осевой линии прямой катушки при достаточно большой ее длине можно опреде­лить по следующей приближенной формуле:

.                                                (7.11)

Ошибка при определении Н будет тем меньше, чем больше отношение длины катушки к ее диаметру. Магнитная индукция прямой катушки

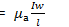                                                 (7.12)

§ 7.6. Сила взаимодействия токов двух параллельных проводов

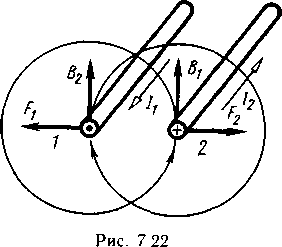
1. Направление и значение силы взаимодействия. Опытным путем установлено, что магнитное поле действует на провод с то­ком, помещенный в поле, с некоторой силой F,называемой элект­ромагнитной. На практике часто встречается параллельное рас­положение проводов стоками, например в линиях электропередачи. Рассмотрим действиеэлектромагнитных  сил           в         системе двух па­раллельных прямолинейных проводов1и2длиной l, располо­женных на расстоянии а друг от друга. Токи l₁ и l ₂ указанных проводов направлены в одну сторону (рис. 7.21) или в противо­положные (рис. 7.22). Проходящий по проводу 2 ток /₂ создает поле, магнитная индукция которого на оси провода 1 выражается формулой (7.6):                                                 

 

 

Направление вектора индукции В₂определяется по правилу буравчика. Так как в магнитном поле провода 2 находится про­вод I с током I1, то на него действует электромагнитная сила

l

Провод 2с током I2 находится в магнитном поле провода 1 с током I1. Магнитная индукция

а электромагнитная сила

Направление сил F1 и F2определяется по правилу левой руки. Из сказанного следует, что провода с токами одного направления притягиваются друг к другу, а с токами противоположного от­талкиваются друг от друга с силой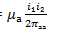

 

 

2. Принцип действия ваттметра электродинамической системы.

На принципе механического взаимодействия проводов с электри­ческими токами действуют приборы электродинамической систе­мы. На рис. 7.25 показаны устройство и включение ваттметра электродинамической системы. Неподвижная катушка ваттметра (НК) имеет незначительное сопротивление и включается с прием­никами энергии последовательно. Подвижная катушка (ПК) вместе с добавочным сопротивлением г_д имеет очень большое сопротивление и подключается к приемникам энергии параллельно. Благодаря взаимодейст­вию тока неподвижной катушки I с то­ком подвижной катушки I_и подвижная система прибора вместе с указательной

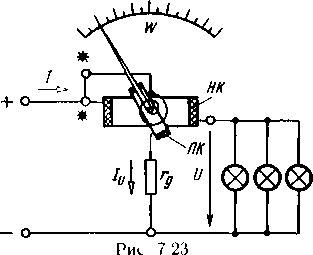
стрелкой повернется на некоторый угол 𝜶, зависящий от силы упру­гости противодействующей пружины. Этот угол пропорционален произведению токов в катушках, т. е. 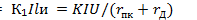.Тогда

,где Р - мощность приемника энергии. Таким образом, угол поворота подвижной системы ваттметра пропорционален мощности приемника энергии.хода и короткого замыкания. Для проведения опытов холостого хода и короткого замыкания требуется сравнительно небольшая мощность источника питания. Поэтому рабочий режим электро­технических устройств большой мощности целесообразно опреде­лять на основании соответствующих опытов холостого хода и ко­роткого замыкания.

Глава 8

ФЕРРОМАГНЕТИЗМ. МАГНИТНАЯ ЦЕПЬ

§ 8.1. Намагничивание и перемагничивание ферромагнитных материалов

1. Кривая первоначального намагничивания и петля гистере­зиса. Ферромагнитные материалы, помешенные в магнитное поле, намагничиваются, т. е. сами становятся источниками магнитного поля. Причина намагничивания заключается в том, что во всех веществах существуют мельчайшие электрические токи, замыка­ющиеся в пределах каждого атома (молекулярные токи). Они вызваны вращением электронов по орбитам и вокруг собствен­ных осей. Магнитные свойства элементарного кругового тока можно характеризовать магнитным моментом т, который равен произведению элементарного тока iи элементарной площадки S, ограниченной контуром элементарного тока. Направление векто­ра mопределяется по правилу буравчика. Магнитные моменты, обусловленные движением электронов по орбитам, называют орбитальными моментами, а обусловленные вращением электро­нов вокруг своей оси — спиновыми моментами.

В ферромагнитных материалах имеются области, называемые магнитными доменами, спиновые моменты которых ориентирова­ны одинаково. Эти области оказыва­ются самопроизвольно намагничен­ными. Ферромагнитное тело состоит из множества доменов, отличающих­ся значением и направлением своих магнитных моментов М. В осталь­ном ненамагниченном стержне маг­нитные домены расположены беспо­рядочно. Вследствие этого их маг­нитные моменты взаимно уравнове­шиваются (рис. 8.1, а) и резуль­тирующая магнитная индукция стержня равна нулю. Если стер­жень поместить в магнитное полё внешнего тока, то магнитные мо­менты доменов повернутся в направлении поля (рис. 8.1, б) и их магнитные поля усилят внешнее магнитное поле. На рис. 8.1, б внешнее поле изображено сплош­ными магнитными линиями, а поля магнитных доменов — пунктирными линиями.

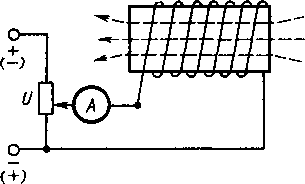
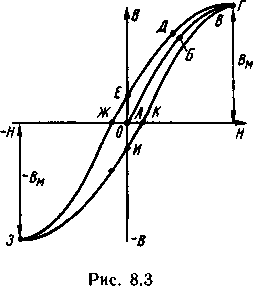
Поместим стержень из ферромагнитного материала в катушку с током (рис. 8.2), а затем, изменяя напряженность поля катуш­ки H = Iw/l,проследим за изменением магнитной индукции В. С увеличением напряженности магнитная индукция сначала быстро возрастает почти пропорционально напряженности поля Н (отрезок АБ на рис. 8.3). На участке БВ рост магнитной ин­дукции замедляется, так как сокращается количество согласо­ванно ориентированных доменов, усиливающих магнитное поле катушки. На участке ВГ, когда по направлению поля повернуты все домены, наступает магнитное насыщение стержня, т. е. такое состояние ферромагнитного вещества, при котором рост напря­женности поля не влечет за собой увеличения магнитной индук­ции.

 

 

Таким образом, магнитный материал можно намагничивать только до определенного состояния. Кривая АБВГ называется кривой первоначального намагничивания, которой пользуются при расчете магнитных цепей электрических аппаратов. При уменьшении напряженности поля стержень размагничивается и его индукция уменьшается по кривой ГДЕ.

Все ферромагнитные материалы стремятся сохранить возбуж­денное магнитное состояние, поэтому кривая их размагничивания лежит выше кривой первоначального намагничивания. Размагни­чивание стержня (сердечника) как бы запаздывает по сравнению с уменьшением напряженности поля. Это явление называется магнитным гистерезисом. После отключения тока катушки (когда Н — 0) магнитная индукция равна величине, называемой оста­точной индукцией (изображена отрезком АЕ на рис. 8.3). Если изменить направление тока в катушке и увеличивать напряжен­ность поля, то стержень сначала будет размагничиваться по кри­вой ЕЖ.Значение напряженности поля обратного направления (отре­зок АЖ на рис. 8.3), при котором магнитная индукция равна нулю, называют коэрцитивной (задерживающей) силой. При дальнейшем увеличении напряженности стержень перемагничи- вается до насыщения (точка 3). Кривая размагничивается ЗИ не совпадает с кривой ЖЗ из-за гистерезиса. Отрезок АЕ = —АИ служит мерой остаточного магнетизма в испытуемом стержне. При вторичном изменении направления тока магнитная индукция стержня изменяется по кривой ИК.Г. Таким образом, при измене­нии направления тока магнитная индукция стержня изменяется по кривой ГДЕЖЗИКГ.

Рассмотренный цикл перемагничивания ферромагнетика на­зывается гистерезисным циклом (петлей гистерезиса). Так как при намагничивании ферромагнитный стержень был Доведен донасыщения, то полученная петля называется предельной петлей гистерезиса. При меньших пределах изменения напряженности внешнего магнитного поля можно получить семейство петель гис­терезиса, заключенных внутри предельной петли (рис. 8.4, а). Кривая 0-1-2-3-4, проведенная через вершины всех петель гисте­резиса, называется основной кривой намагничивания. Она прак­тически совпадает с кривой первоначального намагничивания. Перемагничивание ферромагнитных материалов сопровождается их нагревом, а следовательно, потерей некоторой энергии. Из­вестно, что количество энергии, теряемой в ферромагнитном теле за полный цикл перемагничивания, пропорционально площади петли гистерезиса.

2.Классификация ферромагнитных материалов. Все ферро­магнитные материалы разделяются на магнитомягкие и магнито­твердые. Магнитомягкие материалы (электротехническая сталь, чугун, пермаллой, ферриты и т. д.) обладают малой остаточной индукцией и коэрцитивной силой и имеют круто поднимающуюся основную кривую намагничивания (кривые 1, 2 на рис. 8.4, б). Поэтому они легко перемагничиваются и имеют незначительные

1. потери энергии от гистерезиса, что удобно для использования их в машинах и приборах переменного тока. Для изготовления постоянных магнитов применяются магнитотвердые материалы (закаленная сталь, сплавы: альнико, альниси, магнико и т.д.), обладающие большой остаточной индукцией, коэрцитивной силой и полого поднимающейся основной кривой намагничивания (кривая 3 на рис. 8.4, б). Таким образом, зависимость магнитной индукции от напряженности поля достаточно сложная и не мо­жет быть выражена простой расчетной формулой. Поэтому при расчете магнитных цепей, содержащих ферромагнитики, приме­няют экспериментально снятые кривые намагничивания В(Н) для заданных магнитных материалов.

§ 8.2, Законы магнитной цепи

1. Закон Ома для магнитной цепи. Устройство, содержащее сердечники из ферромагнитных материалов, через которые замы­кается магнитный поток, называется магнитной цепью.

Различают неразветвленные и разветвленные магнитные цепи. Неразветвленная магнитная цепь называется однородной, если все ее участки выполнены из одного материала и имеют по всей длине одинаковое поперечное сечение Разветвленные магнитные цепи могут быть симметричными и несимметричными

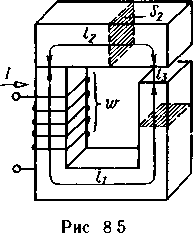
На рис. 8.5 показана неразветвленная, неоднородная магнит­ная цепь, состоящая из трех участков. Под действием магнито­движущей силы Iwобмотки в цепи возникает магнитный поток Ф, который можно принять одинаковым для всех участков. Выбе­рем контур по средней линии магнитной индукции и обозначим длины однородных участков I_и I ₂, I з, а попереченые сечения уча­стков Si, S₂, S3.

 

 

§ 8.2, Законы магнитной цепи

2. Закон Ома для магнитной цепи. Устройство, содержащее сердечники из ферромагнитных материалов, через которые замы­кается магнитный поток, называется магнитной цепью.

Различают неразветвленные и разветвленные магнитные цепи. Неразветвленная магнитная цепь называется однородной, если все ее участки выполнены из одного материала и имеют по всей длине одинаковое поперечное сечение Разветвленные магнитные цепи могут быть симметричными и несимметричными

На рис. 8.5 показана неразветвленная, неоднородная магнит­ная цепь, состоящая из трех участков. Под действием магнито­движущей силы Iwобмотки в цепи возникает магнитный поток Ф, который можно принять одинаковым для всех участков. Выбе­рем контур по средней линии магнитной индукции и обозначим длины однородных участков I _и I ₂, I з, а попереченые сечения уча­стков S₁, S₂, S3.По закону полного тока составим уравнение 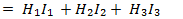Напряженности магнитного поля участков:

 , а магнитные индук­ции: . Теперь напряженности и магнитные индукции подставим в уравнение закона полного тока:

 

 

 

 

По аналогии с электрической цепью

l/(𝝁ₐS) называют магнитным сопротив­лением участка магнитной цепи и обоз­начают Rм· В СИ единица магнитного

сопротивления [

Таким образом I 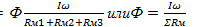      (8.1)

 

Последняя формула выражает закон Ома для неразветвленной магнитной це­пи: магнитный поток прямо пропорцио­нален магнитодвижущей силе (Iw) и об­ратно пропорционален полному сопротив­лению магнитной цепи (ΣRм).Магнитные цепи в электрических машинах, электроизмерительных приборах, реле и других устройствах стремятся выполнить преимущественно из ферромгнитных материалов, а воздушные зазоры сократить до минимума. Это позволяет уменьшать магнитное сопротивление цепи и получить необходимый для работы устройств магнитный поток при наименьшей МДС.

 

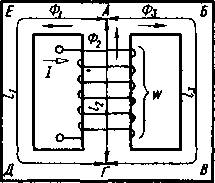
3. Законы Кирхгофа для магнитных цепей. На рис. 8.6 показана разветвленная симметричная маг­нитная цепь, состоящая из двух одинаковых контуров. Средний стержень вместе с катушкой — источником намагничивающей силы — одинаково входит в оба контура. В узле А магнитный поток среднего стержня Ф₂ делится на два равных потока Ф₁ и Фз, если магнитное сопротивление обоих контуров одинаково. Разветвленная магнитная цепь называется симметричной, если ф₁=ф₃. Таким образом,

4.

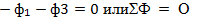                      (8.2)

 

алгебраическая сумма магнитных потоков в узле магнитной цепи равна нулю. Соотношение (8.2) аналогично уравнению для узла электрической цепи, написанному согласно первому закону Кирхгофа:Σ I =0. Для любого контура разветвленной магнит­ной цепи можно также составить уравнения по закону полноготока:

 

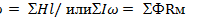                       (8.3)

 

т. е. в контуре магнитной цепи алгебраическая сумма магнито­движущих сил равна алгебраической сумме магнитных напряже­ний на отдельных участках.

Уравнение (8.3) аналогично уравнению для контура электри­ческой цепи = 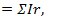 составленному на основании второго зако­на Кирхгофа при постоянном токе. Например, для контура АБВГА (рис. 8.6) 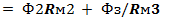. Расчет магнитных цепей, если можно пренебречь потоками рассеяния, аналогичен расчету нели­нейных электрических цепей, причем МДС Iωсоответствует ЭДС E, потоку Ф — ток I и магнитному сопротивлению R_м — электри­ческое сопротивление r. Необходимо иметь в виду, что приведен­ная аналогия магнитных и электрических цепей формальна, т. е. аналогия формул не соответствует аналогии процессов.

 

 

 

 

§ 8.3. Расчет магнитных цепей

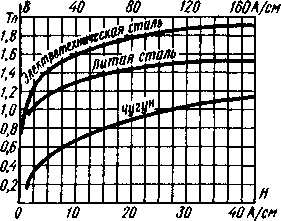
Расчет неразветвленных магнитных цепей. Расчет неразветвленной магнитной цепи (см. рис. 8.5) в большинстве случаев сво­дится к определению намагничивающей силы Iw,которая требует­ся для получения заданного магнитного потока Ф или магнитной индукции В. При этом указываются размеры и материал всех участков магнитной цепи. Такой расчет производят следующим образом, а) Проводят среднюю магнитную линию и по ней цепь разбирают на однородные участки (т. е. одинакового поперечного сечения и магнитной проницаемости р_а). Длины участков l₁, l₂, l₃(в СИ) выражают в метрах (м), а их поперечные сечения S₁, S₂, S₃ — в квадратных метрах (м). б) По формуле В = Ф/S нахо­дят магнитные индукции участков, в) Определяют необходимую напряженность поля Н, а затем магнитное напряжение Hlкаждого участка. Для участков, выполненных из ферромагнитного материа­ла, напряженность поля определяют по кривым намагничивания (рис. 8.7), а для воздушных зазоров—по формуле 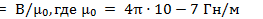. Если индукцию выразить в Тл, в напря­женность— в А/м, то H = 0,8·10⁶ В, г) Складывая магнитные напряжения Hlвсех участков, по закону полного тока опреде­ляют намагничивающую силу, необходимую для создания в данной магнитной цепи потока Ф: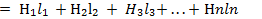

 

Электротехническая (листовая) стало и чугун Литая стало Рис. 8.7

рис 8.6

 

1. Расчет разветвленных магнитных цепей. Порядок расчета разветвленных магнитных цепей рассмотрим на следующем при­мере. В крайних стержнях сердечника (рис. 8.9), выполненного из электротехнической стали, требуется получить магнитную индукцию B₂= 1,2 Тл. Для вычисления намагничивающей силы Iwконтур АБВГА разобьем на два участка и определим длину и сечение каждого из них:    l ₁ = 100 мм=0,1 м; S₁=50·60=

= 3000 мм² = 3·10^⁻3 м²; l₂ = 440 м = 0,44 м; S₂ = 40·50 = 2000 мм²=2·10⁻³м². Магнитный поток правого стержня Ф₂ = B₂S₂= 1,2·2·10⁻³ = 2,4·10⁻³ Вб. Так как магнитная цепь симметрична, то магнитный поток среднего стержня Ф₁ = 2Ф₂ = =2·2,4·10^⁻3=4,8·10^⁻3 Вб, а магнитная индукция B₁=Ф₁/S₁=4,8·10⁻³/(3·10⁻³)=1,6 Тл. По кривой намагничивания электро­технической стали находим напряженность магнитного поля: H₁=44 А/см=4400 А/м и Н₂=10 А/см=1000 А/м (см. рис. 8.7). Значит, Iw = H₁l₁+ H ₂ l ₂ = 4400 · 0,1 + 1000·0,44=880 А.

 

§ 8.4. Электромагниты и реле

1.Подъемная сила элект­ромагнита. Простейший электромагнит (рис. 8.10) состоит из стального сердеч­ника С, на котором разме­щается катушка. Магнитный поток, создаваемый током катушки, замыкается по сер­дечнику и стальному якорю R. В результате сердечник и якорь намагничиваются.При этом против северного полюса сердечника расположен южный полюс якоря, а против южного полюса сердечника — северный полюс якоря. Поэтому якорь будет притягиваться к неподвижному сердечнику. Сила, необходимая для отрыва якоря от сердечника, называется отрывной. Значение отрывной силы (Н)

Если сила выражена в килограммах, магнитная индукция — в теслах, площадь — в квадратных сантиметрах, то F =4 B²S. Сердечник и якорь электромагнита изготовляют из мягкой стали, поэтому при размыкании цепи они размагничиваются и сила ста­новится равной нулю. Электромагниты широко применяют в устройствах автоматики, телемеханики, связи, измерительной техники и т. д.

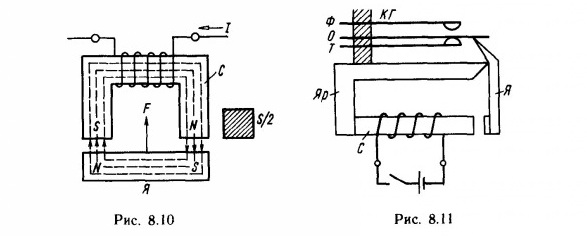
2.Устройство и применение электромагнитных реле. На ис­пользовании электромагнита основано устройство электромаг­нитного реле. Простейшее реле автоблокировки, схематически изображенное на рис. 8.11, состоит из сердечника С с обмоткой, якоря R, ярма Rр и контактной группы КГ, имеющей осевой О, фронтовой Ф и тыловой Т контакты. При отсутствии тока в об­мотке реле якорь под действием противовеса (на рис. 8.11 не показан) отпадает, осевой контакт контактной группы касается тылового контакта. При наличии тока в обмотке реле якорь притянут к сердечнику, осевой контакт касается фронтового.

еле широко применяют­ся в различных автоматиче­ских устройствах, например в железнодорожной авто­блокировке. Рассмотрим ее простейшую схему. Рельсо­вая колея делится на участ­ки, отделяемые друг от дру­га изолирующими стыками (рис. 8.12). По рельсам каждого участка проходит ток, источником которого является путевая батарея ПБ, а приемником — путевое реле ПР. Когда участок свободен от подвиж­ного состава, ток путевой батареи проходит по цепи: +ПБ — ограничительное сопротив­ление ОС — первая рельсовая нить на всю длину участка — обмотка путевого реле ПР — вторая рельсовая нить участка — ПБ. Получая ток, путевое реле удерживает, притянутый якорь. При этом замыкается цепь лампы зеленого огня светофора: + СБ (сигнальной батареи) — осевой и фронтовой контакты реле — лампа зеле­ного огня — СБ. При вступлении поезда на участок рельсовые нити замкнутся между собой через колесные пары,

которые имеют незначительное сопротивление. Ток путевогореле уменьшится, и якорь реле отпадет. При этом осевой контакт соединится с тыловым. В результате в цепь сигнальной батареи вместо зеленой лампы включится красная, указывающая на

занятость участка. Рельсовые нити и скаты поезда имеют неболь­шое сопротивление. Поэтому в рельсовую цепь включают огра­ничительное сопротивление ОС, уменьшающее ток путевой батареи при занятом участке.

Путевое реле, показанное на рис. 8.11 и 8.12, называют нейтральным, так как его якорь притягивается к сердечнику независимо от направления тока. Кроме нейтральных применяют­ся и поляризованные реле. Их якорь отклоняется от нейтраль­ного положения в одну или другую сторону в зависимости от направления тока в его обмотке.

 

 

Глава 9

 

ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ

§ 9.1. Явление электромагнитной индукции.

Значение индуцированной электродвижущей силы

1. Электродвижущая сила в проводе и контуре. В проводе, ко­торый при движении в магнитном поле пересекает магнитные ли­нии, возбуждается электродвижущая сила (ЭДС) электромаг­нитной индукции. Это явление было открыто английским ученым М. Фарадеем в 1831 г. и названо электромагнитной индукцией. Английский физик Д. Максвелл, анализируя результаты опытов М. Фарадея, установил, что ЭДС электромагнитной индукции, наводимой в контуре, равна скорости изменения сцепленного с ним магнитного потока.На рис. 9.1 показана рамка из проводникового материала в однородном магнитном поле. Если эту рамку перемещать вверх или вниз по направлению магнитных линий, влево или вправо под прямым углом к ним, то пронизывающий ее магнитный поток изменяться не будет. ЭДС и ток в рамке при этих условиях не возникают. В рассматриваемом примере отдельные части рамки пересекают линии магнитной индукции и в них имеются ЭДС. Однако полная ЭДС рамки, равная сумме ЭДС, возникающих в отдельных ее частях, равна нулю. Предположим теперь, что рам­ка будет вращаться вокруг оси 00₁. В положении, показанном на рис. 9.1, рамку пронизывает максимальный магнитный поток, который при повороте на 90° будет равен нулю. Следовательно, магнитный поток рамки изменяется и в ней появится ЭДС.

 

 

2.Действие электромагнитных сил. Рассмотрим появление ЭДС индукции в прямолинейном проводнике (рис. 9.2), который перемещается в однородном магнитном поле по медным шинам А и Б в направлении силы Fсо скоростью и. Вместе с проводни­ком перемещаются его элементарные электрически заряженные частицы — свободные электроны и положительные ионы. Следо­вательно, на каждую заряженную частицу будет действовать электромагнитная сила. Пользуясь правилом левой руки, можно установить, что электромагнитные силы, действующие на поло­жительные ионы, направлены к шине Б, а действующие на сво­бодные электроны — к шине А. Таким образом, электромагнит­ные силы стремятся разделить электрически заряженные части­цы, сосредоточив их на противоположных концах проводника. В результате в нем возникает электрическое поле. Силы этого поля и электромагнитные силы направлены в разные стороны. Поэтому разделение электрических зарядов в проводнике проис­ходит до тех пор, пока электромагнитные силы не уравновесятся силами электрического поля. При этом между шинами А и Б воз­никает определенная разность потенциалов, которая при разомк­нутом рубильнике Р равна ЭДС индукции. При замыкании ру­бильника Р в замкнутом контуре появится ток I, его сила будет определяться индуцированной ЭДС и сопротивлением цепи. Этот ток, взаимодействуя с магнитным полем, создает тормозную силу F_T.Следовательно, для перемещения проводника к нему должна быть приложена сила F,равная и направленная противоположно тормозной силе F_T.Чем меньше сопротивление приемника r, тем больше ток контура I, силы F_Tи F.

 

3.Направление ЭДС индукции. Направление ЭДС индукции в прямолинейном проводнике определяется по правилу правой руки: если ладонь правой руки нужно расположить так, чтобы магнитные линии входили в нее, а отогнутый под прямым углом боль­шой палец указывал направление движения проводника, то вы­прямленные четыре пальца руки укажут направление индуциро­ванной ЭДС (рис. 9.3). Русский академик Э. X. Ленц сформули­ровал общее правило, устанавливающее направление наведенной ЭДС: при изменении магнитного потока, пронизывающего контур, в последнем возникает ЭДС такого направления, что обусловлен­ный ею ток противодействует изменению магнитного потока. Рассмотрим пример на применение правила Ленца. На рис. 9.2 замкнутый контур образуется движущимся проводником, шинами A и Б и нагрузкой r. При движении проводника в направлении силы Fмагнитный поток, пронизывающий этот контур, уменьшает­ся. Для противодействия этому индуцируемый ток создает магнит­ное поле одинакового направления с внешним магнитным полем. Если изменить направление движения проводника, то магнитный поток, пронизывающий замкнутый контур, будет увеличиваться. В этом случае магнитное поле индуцируемого тока направлено навстречу внешнему магнитному полю. Таким образом, чтобы определить направление индуцированной ЭДС, по правилу Ленца сначала определяют направление магнитного поля, создаваемое индуцируемым током. Затем по правилу буравчика определяют направление индуцируемого тока и ЭДС.

4.ЭДС индукции. Допустим, что прямолинейный проводник длиной l движется в однородном магнитном поле со скоростью vперпендикулярно магнитным линиям (см. рис. 9.2). За время d t проводник пройдет путь db. При этом на перемещение проводни­ка затрачивается работа dА = Fdb.При равномерном движении внешняя сила равна тормозной: F= F_T= BIl.Так как скорость движения проводника ,то .Подставив в форму­лу элементарной работы значения Fи db,получим 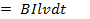. Затраченная на эту работу энергия целиком переходит в элект­рическую: 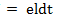, где е — значение ЭДС в проводнике на от­резке пути db.Приравняв правые части последних уравнений, получим . Отсюда ЭДС индукции

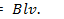                                                    (9.1)

Если проводник движется в плоскости, расположенной под углом к направлению магнитного поля, то индуцируемая ЭДС

 

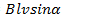                      (9.2)

 

Формулу (9.1) можно преобразовать следующим образом:

 

 

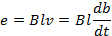
Произведение ldb выражает площадку dS, которую пересекает проводник при своем движении за время dt.Произведение BdSвыражает магнитный поток dФ, который пронизывает площадку dS. Следовательно, наведенная в проводнике ЭДС

 

 

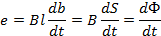
Согласно этой формуле, ЭДС индукции равна скорости изме­нения магнитного потока, пронизывающего контур. Для того что­бы учесть направление ЭДС индукции, перед правой частью ра­венства ставят отрицательный знак, т. е. 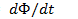.При вы­числении по этой формуле ЭДС индукции имеет положительный знак, если магнитное поле индуцируемого тока направлено в сто­рону внешнего поля. Согласно этому определению, в проводнике (см. рис. 9.2) возникает ЭДС с положительным знаком. Действи­тельно, магнитный поток контура в данном случае уменьшается и скорость его изменения будет отрицательной: 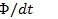,а ЭДС — положительной: 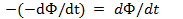.Если проводник(см. рис. 9.2) перемещать в противоположную сторону, то маг­нитный поток контура будет увеличиваться, скорость его измене­ния будет положительной dФ/dt,а ЭДС — отрицательной: е = -dФ/dt.

Если в магнитном поле движется рамка, имеющая wвитков, то ЭДС индукции

Произведение ωdФ называется элементарным потокосцеплениемdψи поэтому

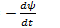                                      (9.3.)

Таким образом, ЭДС индукции в контуре равна скорости изменения потокосцеплення этого контура. Формула (9.3) явля­ется исходной для расчета ЭДС индукции во многих электриче­ских устройствах.

5.Преобразование механической энергии в электрическую. Электромеханическое действие магнитного поля и электромагнит­ная индукция используются для преобразования механической энергии в электрическую и обратно. Устройства, с помощью кото­рых эти преобразования осуществляются, называются электриче­скими машинами. Машина для преобразования механической энергии в электрическую называются генератором, а для обрат­ного преобразования — двигателем. На рис. 9.4 представлен про­стейший генератор переменного тока. Между полюсами электро­магнита Nи Sвращается стальной якорь, на поверхности кото­рого расположен виток изолированного провода abcd.