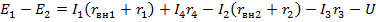Сложные электрические цепи постоянного тока

Общие сведения

Электрические цепи с последовательно-параллельным соеди­нением приемников энергии при питании их от одного источника электрической энергии, а также одноконтурные цепи называют простыми цепями. Расчет этих цепей осуществляется по формулам закона Ома и первого закона Кирхгофа. При этом заданные сопро­тивления часто заменяют одним эквивалентным. Так, цепь на рис. 6.1, а можно привести к элементарному виду с одним экви­валентным сопротивлением г, подключенным к источнику энергии с ЭДС Е₁ (рис. 6.1,6). В данном случае  Электрические цепи с несколькими контурами, состоящими из разных ветвей с произвольным размещением потребителей и источников энергии, называются сложными электрическими цепя­ми. Сложные электрические цепи рассчитывают методами: 1) уз­ловых и контурных уравнений; 2) контурных токов; 3) узлового напряжения; 4) наложения (суперпозиции); 5) эквивале­нтного преобразования тре­угольника и звезды сопротив­лений. В первом методе ис- 'пользуются первый и второй законы Кирхгофа. Первый за­кон был рассмотрен в § 4.3.

Второй закон Кирхгофа

Сложная электрическая цепь(рис. 6.2, а) имеет два узла (Б и Д) и три ветви с токами  .Обозначим контуры цепи I — АБДЕА; II — АБВГДЕА; III — БВГДБ. В контуре АБДЕА включены ЭДС Е₁, Е₁ и сопротивления  на которых созда­ются падения напряжения: , . Если точку А заземлить, то ее потенциал будет равен нулю. 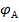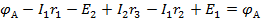Потенциалы точек Б и Д выразятся следующим образом: ;  Если от потенциала  от­нять падение напряжения  и прибавить к нему ЭДС Е₁, то полу­чим потенциал : , или  В левой части полученного равенства оставим ЭДС Е₁ и Е₂, а все остальные его члены перенесем в правую часть. Тогда получим или  В левой части этого уравнения записана алгебраическая сумма ЭДС, действующих в первом контуре, а в правой — сумма падений напряжения во всех сопротивлениях, входящих в этот контур. В общем виде для любого контура

Равенство (6.1) является математическим выражением второго закона Кирхгофа: в любом контуре электрической цепи алгебраиче­ская сумма ЭДС равна алгебраической сумме падений напряжений в отдельных сопротивлениях.

Для каждого контура сложной электрической цепи по второму закону Кирхгофа можно составить

только одно уравнение. При этом особое внимание следует обра­тить на знаки ЭДС и падение напряжения. Вначале произвольно выбирают направление обхода контура. Если действующая в кон­туре ЭДС совпадает с направлением обхода, то ее считают поло­жительной, при обратном направлении ЭДС отрицательна. Паде­ние напряжения на сопротивлении считают положительным, если направление тока в нем совпадает с направлением обхода контура

В электрических цепях встречаются элементы с выводами, на которых имеются напряжения U (сеть напряжения, делитель напряжения и т. д.). В этом случае удобнее использовать следую­щую форму записи второго закона Кирхгофа: . При этом ЭДС напряжения и токи, положительные направления кото­рых совпадают с направлением обхода контура, записываются в соответствующую часть уравнения с положительным знаком. В противном случае эти же величины записываются с отрицатель­ным знаком. Например, для контура (рис. 6.2, б) при обходе его по часовой стрелке имеем