В методе узловых и контурных уравнений применяются два закона Кирхгофа. Пусть сложная цепь (рис. 6.2, а) имеет следующие данные: Е1 = 100 В, Е2 = 50 В, r1 = r2 = 10 Ом, r3 = r4 = 20 Ом. Требуется определить токи 
в ветвях. Сначала на схеме укажем их направления. Токи 
направим к узловой точке Б, а ток 
— от нее. Указанные направления токов выбирают произвольно и условно считают положительными. После этого составим уравнения по законам Кирхгофа, число которых должно быть равно числу неизвестных токов. В данном случае требуются три уравнения. Сначала составляют более простые уравнения по первому закону Кирхгофа. Их число всегда на единицу меньше числа узлов цепи. В схеме, изображенной на рис. 6.2, а, имеется два узла: Б и Д. К узлу 6 подходят токи , а отходит от него ток . Поэтому
(6.2)
Недостающие уравнения составляют по второму закону Кирхгофа. Для контура АБДЕА
. Подставив сюда числа известных величин, получим
.
Наконец, после сокращения на 10 будем иметь
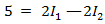(6.3)
Третье независимое уравнение можно составить для контура БВГДБ: 
. Подставив в это уравнение числа известных величин, получим
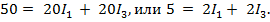(6.4)
Для того чтобы контурные уравнения были независимыми, их составляют по следующему правилу: каждое очередное уравнение должно составляться для контура, отличного от предыдущих хотя бы одной новой ветвью. Итак, составив три независимых уравненияв которых неизвестными являются токи , и решив их, найдем искомые токи. Значение тока 
(рис. 6.2, а) подставим в (6.4). Тогда получим 
Отсюда
. (6.5)
Полученный ток 
подставим в (6.3): 
или 
Отсюда 
.Из (6.5) 
а из (6.2) 
После решения получены токи 
и с положительным знаком. Значит, действительное направление этих токов совпадает с выбранным направлением, указанным на схеме стрелками (рис. 6.2,а). Если какой-либо ток при расчете окажется отрицательным, то из этого следует, что он в действительности проходит в направлении, противоположном выбранному. В данном примере ток получился равным нулю потому, что разность потенциалов между точками Б и Д оказалась равной ЭДС Е2.
Метод контурных токов
Метод узловых и контурных уравнений в ряде случаев требует больших вычислений. Например, при расчете цепи (рис. 6.3), имеющей три узла (А, В, Г) и пять ветвей, требуется составить и решить систему из пяти уравнений. Число уравненийсистемы можно сократить, применив метод контурных токов. Для расчета по методу контурных токов схему сложной цепи разбивают на отдельные контуры — ячейки. Например, схему рис. 6.3 разбивают на три контура: контур I — АБВЕА, контур II — АЕВДГА и контур III — ВГДВ. Затем каждому контуру приписывают произвольно направленный контурный ток, одинквый для всех участков данного контура.На
рис. 6.3 контурные токи 
отмечены индексами контуров, а токи в ветвях 
— индексами ветвей, причем всем контурным токам дано одно и то же положительное направление — по часовой стрелке. Контурные токи, проходящие по внешним ветвям, являются для них действительными токами, например токи 
Действительные токи внутренних ветвей можно найти как разность токов двух контуров, в которые входит эта ветвь. Так, на рис. 6.3 токи 
Выбрав и указав на схеме направления контурных токов, для каждого контура составляем уравнение по второму закону Кирхгофа. Направление обхода контуров принимается совпадающим с направлением контурных токов. Для схемы рис. 6.3 имеем три уравнения для контуров:
; 
;
.
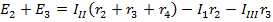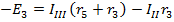Левая часть каждого уравнения =— алгебраическая сумма ЭДС, включенных в контур, а правая — общее падение напряжения в контуре от контурных токов. Подставляя в систему уравнений сопротивления и ЭДС и решая их совместно, находят контурные токи . Токи в ветвях схемы легко определить по контурным токам
Метод узлового напряжения
Определение узлового напряжения и токов. Потребители электрической энергии (лампы, электродвигатели и т.д.) соединяются параллельно. Часто общая мощность включенных приемников становится больше той, которую может отдать в сеть источник энергии. В таких случаях для увеличения мощности при неизменном напряжении источники энергии включают параллельно. При этом получается сложная электрическая цепь, представленная на рис. 6.7. В ней имеется два узла А и Б, к которым присоединяются источники энергии с ЭДС Е1, Е2 и Е3. Сопротивления г1, г2 и г3 можно принять за внутренние сопротивления источников, а сопротивление г4 — за эквивалентное сопротивление всех приемников энергии.
Напряжение между узлами А и Б называется узловым напряжением. Оно равно разности потенциалов узловых точек, т. е. 
. Для расчета подобных сложных электрических цепей обычно пользуются методом узлового напряжения. Выведем формулу этого напряжения. Если ЭДС Е1, Е2 и Е3 больше узлового напряжения, то все источники ЭДС будут работать в режиме генератора, а токи I1, I2 и I3 направлены к узлу А. Ток приемников I4 = I1+ I2+ I3 Для контура, образованного первой ветвью с ЭДС E1 и сопротивлением r1 и четвертой ветвью с сопротивлением г4, составим уравнение по второму закону Кирхгофа: 
. Отсюда ток первого источника
, (6.6)
где g1 = I/r1— проводимость первой ветви. Аналогично определяем токи второго и третьего источников:
; (6.7)
. (6.8)
Ток приемников энергии
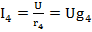; (6.9)
Для узла А напишем уравнение по первому закону Кирхгофа: I4 = I1+ I2+ I3. Подставив в это уравнение найденные выражения для токов, получим 
+ 
+ 
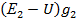. Раскрывая скобки, получим 
или 
.
В общем виде
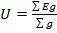. (6.10)
Если какая-либо из ЭДС (рис. 6.7) имеет противоположное направление, то в (6.10) она войдет с отрицательным знаком. Таким образом, узловое напряжение равно алгебраической сумме произведений ЭДС на проводимости соответствующих ветвей, деленной на сумму проводимости ветвей. Обычно бывают заданы все ЭДС и сопротивления. Находят токи методом узлового напряжения следующим образом: 1) по (6.10) определяют узловое напряжение; 2) пользуясь (6.6) — (6.9), определяют токи в ветвях цепи.
2. Анализ расчетных формул. Внимательно изучив (6.6) — (6.10), можно сделать следующие выводы: а) при параллельном соединении источники питания имеют одинаковые токи (I1=I2=I3), если они имеют одинаковые ЭДС (Е1 = Е2 = Е3) и внутренние сопротивления (r1 = г2 = r3 или проводимости g1 = g2 = g3; б) при равных ЭДС, но различных внутренних сопротивлениях наибольший ток имеет источник с меньшим внутренним сопротивлением, т. е. с большей проводимостью g; в) если ЭДС источника равна узловому напряжению U, то его ток 
г) если ЭДС источника окажется ниже узлового напряжения, то ток в его ветви будет направлен - навстречу ЭДС. В этом случае источник ЭДС работает в режиме потребителя энергии (например, при заряде аккумуляторов); д) если увеличить ЭДС первого источника, то возрастут его ток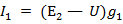 
и узловое напряжение 
В результате этого снизятся токи других источников.
Метод наложения
Метод наложения можно применять для определения токов в цепи, в которой одновременно действуют несколько ЭДС. Этот метод основан на принципе наложения и применим только для линейных цепей. Сущность принципа наложения заключается в том, что ток в любой ветви цепи с постоянными сопротивлениями равен алгебраической сумме частичных токов, создаваемых в этой ветви каждой из ЭДС в отдельности. Например, ток I3 (рис. 6.9, а) равен алгебраической сумме двух токов: I3 (рис. 6.9,6), возникающего в ветви г3 от действия только ЭДС Е1, и I"3 (рис. 6.9, в), возникающего в этой же ветви от действия ЭДС Е2.
При расчете цепей по методу наложения поступают следующим образом.
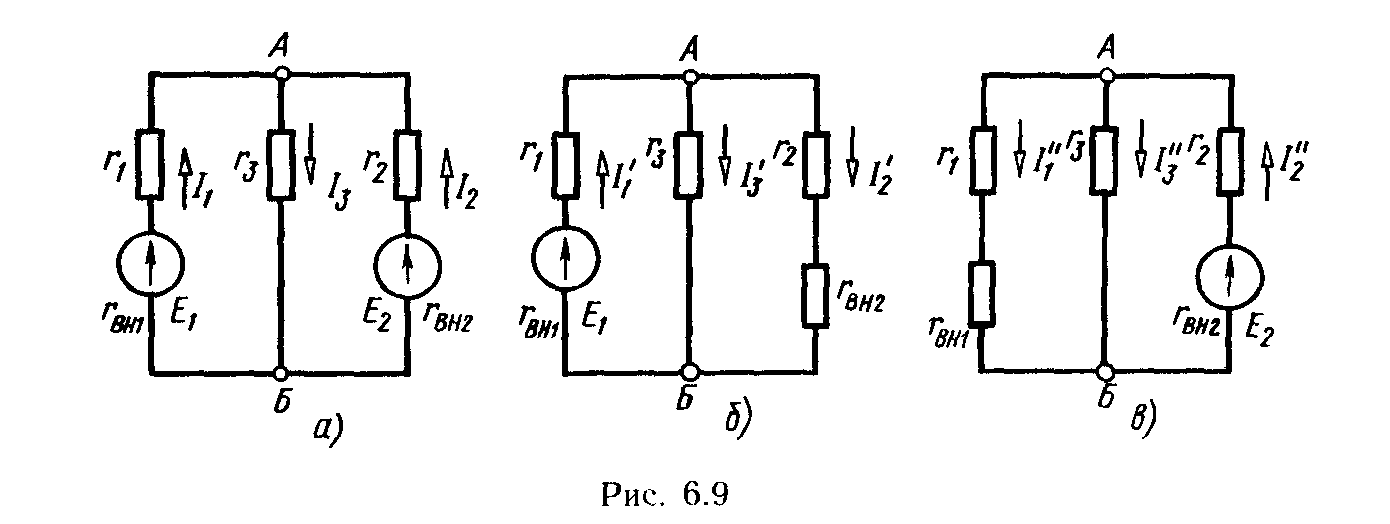
В схеме оставляют первый источник энергии с ЭДС Е1; остальные источники отключают, оставляя в схеме их внутренние сопротивления. Обычно получается цепь с последовательно-параллельным соединением сопротивлений. В этой цепи легко определить так называемые частичные токи, вызванные действием только первого источника ЭДС. Их обозначают I”1, I”2, I”3 и т. д.
В схеме оставляют второй источник энергии с ЭДС Е2; остальные источники исключают, оставляя в схеме их внутренние сопротивления. В результате расчета определяют частичные токи от действия второго источника ЭДС: I”1, I”2, I”3 и т. д.
Аналогично производят расчеты для всех ЭДС схемы.
Алгебраически сложив частичные токи, определяют действительные значения токов на каждом участке сложной цепи, когда все ЭДС действуют одновременно. Знак, который ставится перед частичным током при алгебраическом сложении, зависит от того, совпадает ли направление этого тока с выбранным положительным направлением тока в ветви или противоположно ему.
