С точки зрения математики в моделях системной динамики нет ничего, кроме переменных и констант, дифференциальных уравнений и функциональных зависимостей. Поэтому формально для разработки таких моделей достаточно средств, которые позволяют строить модели динамических систем, с возможностью представления формул, алгебраических и дифференциальных уравнений, а также различных функций (как встроенных, так и определяемых пользователем). Одной из типичных функций, широко используемых в моделях системной динамики (в частности, в задачах логистики), является функция задержки. Такая функция delay (х, t) включена в состав встроенных функций AnyLogic. Описание этой функции можно найти в справочнике классов (класс Func).
Поскольку AnyLogic включает все указанные выше средства, разработка моделей системной динамики на платформе AnyLogic происходит практически
так же, как и в специализированных инструментах, специально созданных для этой области. Однако есть существенная разница в подходах при разработке моделей системной динамики и моделей динамических систем. Эта разница состоит в том, что разработчики моделей системной динамики мыслят не в терминах дифференциальных и алгебраических уравнений. Они мыслят совсем другими категориями. А именно, при создании модели они мыслят в терминах графических представлений поточных диаграмм, в терминах функциональных зависимостей переменных, структуры связей переменных и вообще не используют терминологию дифференциальных уравнений.
Кроме того, с точки зрения системной динамики все системы, какими бы сложными они ни были, построены на замкнутых циклах обратной связи зависимостей переменных системы. Поэтому графическое отображение потоковых диаграмм, а также связей переменных, на основе которых можно анализировать циклы зависимостей параметров, является для системной динамики важнейшим требованием.
В AnyLogic существуют средства, позволяющие эффективно разрабатывать модели системной динамики и графически представить потоковые диаграммы, связи и зависимости переменных системы. Мы рассмотрим эти средства и методику разработки системно-динамических моделей в AnyLogic на нескольких примерах.
Модель развития эпидемии
На рис. 13.5 изображена модель развития эпидемии гриппа, описанная в разд. 13.1. Все элементы, представленные в поле редактора, вводятся как переменные. Переменные susceptible, infected и recovered, определяющие количества людей на разных стадиях болезни (еще не заболевшие, заболевшие и выздоровевшие соответственно), являются накопителями в терминах системной динамики. Они определяются в модели AnyLogic как переменные вида "Интеграл или накопитель", а в поле редактора они будут автоматически представлены как стилизованные квадратики  . Интен-
. Интен-
сивности get_sick и get_well определены как переменные, заданные формулами. В поле редактора их пиктограмма автоматически представляется в виде вентилей. Вспомогательные переменные системной динамики задаются переменными AnyLogic. Константы модели могут быть представлены также параметрами.
После щелчка по кнопке  панели инструментов в окне редактора поя-
панели инструментов в окне редактора поя-
вятся стрелки, показывающие потоки, а также голубые стрелки, отражающие зависимости между переменными модели (рис. 13.5). Эти отношения зависимостей в AnyLogic автоматически вычисляются на основании определения переменных, введенных разработчиком.
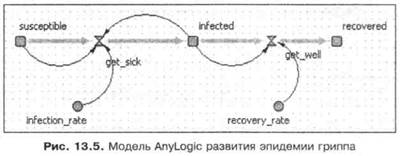
Рисунок 13.5 полностью идентичен рис. 13.1, на котором представлена та же модель, но построенная в традиционных пакетах моделирования. Построение моделей системной динамики в AnyLogic удобно выполнять в два этапа. На первом в поле редактора помещаются все переменные, а на втором этапе для каждой переменной определяется ее вид и конкретная функциональная зависимость с помощью мастера функций — выпадающего окна, в котором появятся кроме стандартных функций еще имена переменных и параметров данного объекта, которые к этому времени были определены. Окно это открывается щелчком по кнопке мастера функций  (рис. 13.6).
(рис. 13.6).


13.5. Пример модели, представляющей сложные взаимные зависимости переменных: модель Лоренца
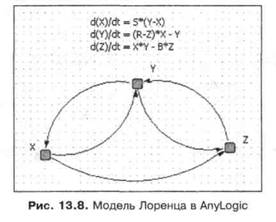
Эта знаменитая модель была построена Эдвардом Лоренцем (Edward Lorenz [EL63]) для упрощенного описания процессов, происходящих в атмосфере и определяющих погоду. Модель описывает зависимости трех переменных переменная х задает интенсивность конвекции, y — это разница температур нисходящего и восходящего потоков, a z — изменение со временем вертикальной температуры в некоторой точке пространства.
С формальной точки зрения модель Лоренца не представляет ничего сложного: это просто три переменных, взаимно связанных системой дифференциальных уравнений. Однако в ней присутствуют три различных петли обратных связей, что делает эту систему трудной для понимания и анализа (рис. 13.8).
Несмотря на кажущуюся простоту системы, аналитического решения у нее нет. Сложные взаимные связи переменных делают динамику модели весьма интересной. Во-первых, при некоторых начальных условиях модель описы-
вает так называемый детерминированный хаос — детерминированную модель, поведение переменных которой чрезвычайно хаотично (другое название модели — аттрактор Лоренца). Во-вторых, эта модель демонстрирует высокую чувствительность к начальным условиям. Например, при определенных значениях параметров (x=z=s=10, y=o, r=28, в=8/з) незначительные изменения в начальных условиях существенно меняют траектории переменных.
Поставим эксперимент. В модели Lorenz weather Model (она находится в папке Model Examples\Part IV) параллельно моделируются два идентичных процесса. Один процесс — с переменными (х, y, z), а другой — его копия с переменными (xi, yi, zi). В обеих моделях для всех переменных и параметров установлены одинаковые указанные ранее начальные значения за исключением начального значения z1, которое отличается от z=10 в десятом знаке, т. е. z1=10.00000001.
Эксперимент на рис. 13.9 показывает, что через некоторое время после старта значения x1 начинают существенно отличаться от значений х. Лоренц интерпретировал этот эффект так: даже взмах крыла бабочки где-нибудь в лесах Бразилии может через месяц вызвать ураган в Техасе. Лоренц назвал его эффектом бабочки. Другой вывод из этой модели состоит в том, что нельзя рассчитывать на точность долговременных прогнозов погоды: все измерения делаются с некоторой погрешностью, в пределах которой процессы в атмосфере могут развиваться со временем в совершенно различных направлениях. Иными словами, точность предсказаний погоды объективно ограничена.
Модели системной динамики, построенные для анализа реальных экономических и бизнес-процессов, процессов урбанизации, динамики народонаселения и т. п., обычно значительно сложнее этой модели Лоренца. Перекрестное взаимное влияние процессов в них иногда может вызвать совершенно неожиданные эффекты, похожие на эффект детерминированного хаоса,
описываемый моделью Лоренца. Дж. Форрестер в работе [JF69] пишет о том. что большая корпорация, город, экономика, правительство — все это примеры сложных систем, поведение которых в корне отличается от того, что мы обычно предполагаем из опыта наблюдения простых систем. Модель Лоренца демонстрирует возможность возникновения хаотического поведения в подобных системах, в которых существуют перекрестные причинные связи переменных. Одна из задач моделирования — предсказать такие ситуации и ввести управления, предотвращающие хаотическое развитие процессов и направляющие их в желаемое русло.







