Системная динамика выработала свою графическую нотацию для построения структур потоковых диаграмм (stock-and-flow диаграмм), представляющих причинно-следственные связи в сложной системе. Такая нотация реализована в нескольких существующих на рынке коммерческих пакетах моделирования (Stella, Vensim, iThink, Powersim и других), позволяющих графически разрабатывать и анализировать системно-динамические модели. Графическая нотация для спецификации связей в упомянутых пакетах моделирования и возможности этих инструментов очень близки. Эта нотация включает простые графические элементы с ясной семантикой, которая позволяет по построенной графической схеме взаимных зависимостей переменных и параметров системы очень просто строить уравнения ее динамики и проигрывать их во времени.
Рассмотрим пример. На рис. 13.1 изображена структура классической модели распространения эпидемии, построенная в графических редакторах инструментов моделирования Stella и Powersim. В этой модели исследуется зависимость динамики числа заболевших (например, гриппом) и выздоровевших после болезни. Здесь обозначены:
□ susceptible — общее число людей, восприимчивых к гриппу (т. е. не
вакцинированных);
□ infected — общее число людей, заболевших гриппом к некоторому моменту времени;
□ recovered — число людей, выздоровевших после болезни гриппом;
□ infection_rate — доля заболевающих гриппом в единицу времени (от О до 1) среди восприимчивых к гриппу людей;
□ recovery_rate — доля выздоравливающих в единицу времени (от 0 до 1) среди всех людей, заболевших гриппом;
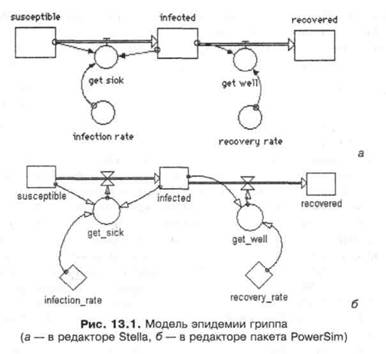
□ get_sick — число людей, заболевших в единицу времени;
□ get_well — число людей, выздоровевших в единицу времени.
Фактически, графическая структура рис. 13.1 выражает следующие функциональные зависимости, которые автоматически формируются в пакетах поддержки моделирования Stella и Powersim по графическому представлению модели:
d(susceptible)/dt = - get_sick;
d(infected)/dt = get_sick - get_well;
d(recovered)/dt = get_weli;
get_sick = f(infected, susceptible, infection_rate);
get_well = f(infected, recovery_rate).
Эта модель может представлять и разностные уравнения, например первое уравнение:
susceptible(t+At) = susceptible(t) - get_sick * At
Дополнительно в моделях должен быть определен конкретный вид функциональных зависимостей интенсивности заболевания и интенсивность выздоровления, который не может быть выражен графически. Например, для
модели эпидемии на основе мнения экспертов были определены следующие конкретные функциональные зависимости:
get_sick = infected * susceptible *infection_rate get_well = infected * recovery_rate
После построения графической модели, определения функциональных зависимостей и задания начальных значений переменных и констант, модель может быть запущена на выполнение, и динамика ее поведения исследована, например, на чувствительность к изменению параметров.
Итак, в потоковых диаграммах системной динамики используется четыре базовых графических объекта: накопители (уровни, переменные состояния потоки (связи между накопителями, вентили, регулирующие потоки, функциональные зависимости, определяющие взаимное влияние потоков). Накопители обозначаются прямоугольниками, потоки — направленными переходами, а вспомогательные переменные — кружками. Стрелки обозначают причинно-следственные зависимости в модели. Накопитель — это параметр, содержащий нечто. Поток — это непрерывное перемещение содержимого между накопителями. Накопители и потоки влияют друг на друга через связи. которые могут формировать цепи положительных и отрицательных обратных связей. Для задания влияний параметров используются вспомогательные переменные, обозначаемые кружками. Временная задержка моделируется блоками задержки. Параметры-константы в некоторых системах моделирования изображаются ромбиками (см. рис. 13.1, б).
Петли причинных связей отражают влияние некоторого процесса а на процесс в. Процесс в, в свою очередь, может также влиять на а, возможно, через длинную цепочку причинно-следственных связей. Изучение процессов а и в по отдельности невозможно. Только изучение динамики всей системы со всеми ее связями и временными задержками может привести к корректному пониманию процессов развития системы. Это и составляет основную идею системного мышления. Многие авторы непосредственно связывают системную динамику с системным мышлением в экономике, социальной сфере и экологии.
В сложных моделях системной динамики ясно проявляется одна из главных причин моделирования: непосредственное влияние каждого конкретного процесса на другие процессы можно понять, проанализировать, описать и изобразить графически. Однако взаимное влияние многих процессов человек понять не может, только имитационное моделирование и компьютерный эксперимент дают возможность понять и оценить взаимное влияние каждого процесса на любой другой, даже если они не связаны непосредственно, а также влияние параметров процессов на важные системные характеристики.
Дж. Форрестер пишет, что воспитанная на наблюдении и использовании простых систем, наша интуиция не способна правильно оценить последствия
тех или иных корректирующих действий в сложных системах. Простые системы обычно характеризуются только одной петлей обратной связи, имеют только одну основную переменную состояния. Примером является система управления, рассмотренная в предыдущей главе, в которой только одна переменная — температура бойлера — является основной переменной состояния. Интуитивный урок, который получают люди при использовании таких систем, тот, что причина и следствие тесно связаны и ясны. Более того, искусственные технические системы, используемые людьми, обычно создаются такими, чтобы управление ими отвечало тому же требованию. Например, хотя автомобиль отнюдь не является простой системой, специально разработанная система управления им обеспечивает простую и ясную причинно-следственную связь управляющих воздействий и характеристик движения. Многие природные и искусственные системы, однако, не обладают такими свойствами. Каскадное отключение производящих мощностей в электроэнергетических сетях, развивающиеся процессы перенаселенности мегаполисов, социальные процессы в обществе ("оранжевые" революции) — все это примеры процессов в сложных системах, в которых нет простых связей между причинами и следствиями.
В сложных системах существует несколько петель обратных связей параметров как положительных, так и отрицательных, и причины изменений состояний системы могут лежать далеко от следствий как во времени, так и в пространстве. Часто за причину некоторого эффекта в таких системах люди принимают то, что Дж. Форрестер называет "симптомом" — промежуточную характеристику системы, непосредственно связанную с этим эффектом в длинной цепочке причинно-следственных связей. Очевидно, что для коррекции эффекта воздействие на симптом неэффективно, оно обычно не может устранить причину возникновения эффекта. Задача моделирования — выявить реальные причинные зависимости в сложных системах и найти схемы управления, подавляющие нежелательное развитие событий.






