Глава 12. Динамические системы

Глава 13. Системная динамика

Глава 14. Дискретно - событийное моделирование

Глава 15. Многоагентные системы

Глава 16. Использование

Различных парадигм при разработке моделей

отя имитационное моделирование — чрезвычайно широкая сфера с огром­ным количеством прикладных областей, в каждой из которых существуют свои приемы моделирования, здесь можно выделить четыре основные пара­дигмы моделирования, т. е. четыре основные системы взглядов, подходов и концепций, используемых в качестве каркаса при построении моделей:

□динамические системы,

□ системная динамика,

□ дискретно-событийное моделирование,

□ мультиагентные системы.

За исключением мультиагентного моделирования, три первые парадигмы сформировались более 40 лет назад. За несколько десятилетий эти концеп­ции, фактически, не изменялись, поэтому их часто называют традиционны­ми. Одной из причин стабильности традиционных парадигм моделирования является их удобство для решения проблем моделирования, специфичных для конкретных применений. Другая причина состоит в том, что традици­онные парадигмы "заморожены" в программных продуктах, которые были разработаны в 60-х годах прошлого века и до сих пор широко используются в моделировании. Эти выпущенные на рынок продукты препятствуют рево­люционным изменениям парадигм моделирования.

В данной части на примерах построения типичных моделей из упомянутых четырех областей показывается, что с помощью инструмента AnyLogic раз­работка моделей в соответствии с каждой из перечисленных парадигм вы­полняется легко и естественно. Потому изучение различных парадигм моде­лирования для различных классов проблем может быть выполнено в рамках только одного этого инструмента. Более того, AnyLogic предоставляет воз­можность объединения, смешивания различных методов и стилей модели­рования при создании одной модели, чего нет ни в одном современном продукте имитационного моделирования.

 

Глава 12

Динамические системы

Динамические системы — это сложные объекты, поведение которых описы­вается системами алгебраических и дифференциальных уравнений, а также событиями, меняющими либо среду, либо модель, либо даже саму структуру системы. К этому классу относятся системы управления, физические и ме­ханические объекты, объекты химической технологии, системы обработки сигналов и т. п.

12.1. Простая динамическая система: система управления бойлером

Рассмотрим в качестве примера классическую динамическую систему, со­стоящую из двух связанных подсистем: объекта управления и регулятора (рис. 12.1).

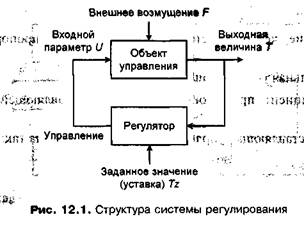
Пусть объектом управления является бойлер, который нагревается до темпе­ратуры т. Величину температуры т необходимо поддерживать на заданном уровне Tz. Температура бойлера зависит от входного параметра — в нашем случае от мощности тока U, подаваемого на нагревательный элемент бойле­ра. Объект управления подвергается внешнему возмущению f (f может ха­рактеризовать внешнюю температуру или теплоизоляцию), вследствие чего значение выходного параметра т может меняться. Поддержание значения т на заданном уровне Tz есть задача регулятора. Регулятор по разнице задан­ного и текущего значений выходного параметра (tz-t) формирует величину входного параметра объекта управления — в нашем случае регулируется мощность U, подаваемая на нагревательный элемент.

Уравнения функционирования как бойлера, так и регулятора будем записы­вать явно, а не с помощью передаточных функций.

Объект управления. Выходная величина т типичного объекта управления описывается уравнением:

dT/dt = 1/а *(k*U - F - Т),

где:

□ a — коэффициент пропорциональности, определяемый параметрами объ­екта управления (выберем его значение 10);

□ k — коэффициент усиления объекта по управлению (установим его в 1);

□   f — изменяющееся внешнее воздействие (температура окружающей сре­ды или теплоизоляция).

Регулятор можно строить разными способами; мы будем использовать здесь так называемый регулятор с пропорционально-интегральным законом управления (ПИ-регулятор). Выходную величину (управление) регулятора определим так:

U=Ui +Kp*(Tz-T),

где^-

□ и — управление, которое состоит из интегральной и пропорциональной
части;

□ Ui — интегральная составляющая управления;

□ Kр- коэффициент при пропорциональной составляющей управления
(=1).

Интегральная составляющая управления может быть задана так:

dUi/dt = Ki*(Tz-T),

где:

□ Ki — коэффициент при интегральной составляющей управления (= 0.3).

Поставим задачу исследовать с помощью модели качество регулирования температуры бойлера в зависимости от соотношений параметров объекта управления и регулятора.