В гидродинамике несжимаемой жидкости устанавливается, что скорости вдоль потока несжимаемой жидкости изменяются обратно пропорционально площадям живых сечений. В условиях сжимаемой жидкости уравнение постоянства массы (рис. 1 – 1)
приводит в некоторых случаях к противоположным выводам.
Представим уравнение в дифференциальной форме. Логарифмируя, а затем дифференцируя его под знаком логарифма, получим:
(1 – 1)
Преобразуем последнее уравнение.
В свою очередь из уравнения изменения количества движения для одномерного движения потока сжимаемой жидкости (уравнения Д. Бернулли в дифференциальной форме) имеем
Тогда
Подставляя значение 
в (1 – 1) и, решая его относительно 
, получим:
Учитывая, что 
, последнее уравнение примет вид:
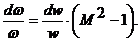(1 – 2)
Это уравнение позволяет сделать следующие выводы. Если число М < 1 (w < a), правая часть уравнения будет отрицательной. Следовательно, знаки перед d w и dw будут противоположными. Это значит, что в дозвуковом потоке, как и в потоке несжимаемой жидкости, скорость w обратно пропорциональна площади живого сечения w.
Если же М > 1, то есть когда w > a, знаки перед d w и dw совпадают. Это значит, что в сверхзвуковом потоке сжимаемой жидкости скорость w прямо пропорциональна площади живого сечения w. То есть следует вывод, прямо противоположный выводу, широко известному из гидродинамики несжимаемой жидкости.
Подобное явление в сжимаемой жидкости возможно потому, что увеличение скорости в нем вызывает не только уменьшение давления (как и в несжимаемой жидкости), но и уменьшение плотности, то есть - её расширение. Следовательно, расширение струи газа в сверхзвуковом потоке ведет к расширению самого газа в термодинамическом смысле, то есть к уменьшению давления, плотности, температуры и к увеличению скорости.
Рассмотрим, в каких условиях возможен переход дозвукового потока в сверхзвуковой и, наоборот, сверхзвукового в дозвуковой.
Пусть имеется поток, в котором w = a, то есть М = 1,0. Из уравнения (1 – 2) следует, что в этом случае 
и что 
. Если при непрерывном изменении скорости течения струи , то это значит, что в данном месте струя переходит от расширения к сужению или, наоборот, от сужения к расширению.
Теперь установим, в каких условиях может наступать равенство w = a (М = 1,0) и переход потока из одного вида в другой.
Рассмотрим две возможные конфигурации потока (струи): расширяющуюся и сужающуюся к середине (рис. 1 - 2).
В первом случае (рис. 1 - 2,а) при дозвуковой скорости потока в начале струи скорость в ней уменьшается в направлении течения и в сечении w max имеет минимальное значение.
При сверхзвуковой скорости потока скорость увеличивается в направлении течения и в сечении w max имеет наибольшее значение. Следовательно, в обоих случаях скорость течения в сечении w max может быть равной скорости звука.
Во втором случае (рис. 1 – 2,б) при дозвуковой скорости потока в начале струи скорость в струе по мере уменьшения площади сечения увеличивается и в сечении w min может стать звуковой, а затем и сверхзвуковой.
При сверхзвуковой скорости потока в начале струи скорость струи по мере уменьшения сечения также уменьшается и в сечении w min может стать звуковой, а затем будет уменьшаться в расширяющейся части струи уже как дозвуковая скорость.
Следовательно, скорость струи может перейти значение скорости звука только в наиболее узком сечении струи. Это сечение называют критическим, а скорость звука, равную скорости течения потока, называют, как указывалось выше, критической скоростью.
Рассмотренную выше особенность струй (потоков) сжимаемых жидкостей (газов) учитывают при проектировании специальных насадок (сопел), например, в ракетостроении, которые должны обеспечить истечение сжимаемых жидкостей со сверхзвуковой скоростью из ёмкостей, где они находятся под давлением.
В честь шведского инженера Лаваля, предложившего для получения сверхзвуковых потоков плавно сужающуюся и затем плавно расширяющуюся насадку (сопло), эту насадку называют сопло Лаваля (рис. 1 - 2,б).
