3.1. ОСОБЕННОСТИ РАСЧЕТА ДВИЖЕНИЯ ГАЗА
Использование газопроводов. Газопроводы используются для перекачивания по трубам газов (воздух, пар, природный и искусственный газы) для различных бытовых и технических целей.
Воздуховоды служат для подачи воздуха к технологическому оборудованию (технические воздуховоды или воздухопроводы) и для вентиляции помещения (вентиляционные воздуховоды).
Газопроводы служат для подачи газа к газораспределительным пунктам (ГРП) и отдельным объектам промышленного и коммунально-бытового назначения (газопроводы среднего и высокого давления), а также для транспортирования газа от ГРП к потребителям и раздачи его внутри зданий.
Паропроводы предназначены для транспортировки пара на предприятиях, использующих пар в качестве технологического продукта или энергоносителя, например, на тепловых или атомных электростанциях, в системах парового отопления и др.
Основные закономерности течения воздуха (газа) такие же, как и для жидкостей, т.е. имеют место ламинарный и турбулентный режимы течения, установившийся и неустановившийся характер течения, равномерное и неравномерное течение из-за переменного сечения трубопровода и все остальные кинематические и динамические характеристики потоков.
Особенности движение газа в трубопроводе. По сравнению с движением капельных жидкостей движение газов характеризуется некоторыми особенностями, обусловленными, главным образом, различием физических свойств капельных и газообразных жидкостей. В рассматриваемом случае возникающие потери напора на трение по длине вызывают ряд характерных особенностей движения реального газа по сравнению с движением по трубам несжимаемых жидкостей.
Вследствие низкой вязкости воздуха и относительно больших скоростей режим течения газов в большинстве случаев турбулентный.
С ростом потерь напора на трение давление по длине трубы уменьшается, что ведет к расширению газа и уменьшению его объемного веса.
Вместе с тем в условиях установившегося движения, когда весовой расход остается постоянным вдоль трубы, уменьшение объемного веса вызывает одновременное увеличение средней скорости течение по трубе.
Изменяется вдоль трубы и коэффициент трения l.
При наличии теплообмена будет иметь место и непрерывное изменение температуры газапо длине трубы.
Особенности расчета движение газа. Инженерные расчеты пневмосистем сводятся к определению скоростей и расходов воздуха при наполнении и опорожнении резервуаров (рабочих камер двигателей), а также с его течением по трубопроводам через местные сопротивления.
Вследствие сжимаемости воздуха эти расчеты значительно сложнее, чем расчеты гидравлических систем, и в полной мере выполняются только для особо ответственных случаев.
Для промышленных пневмопроводов достаточно знать закономерности установившегося характера течения воздуха.
В зависимости от интенсивности теплообмена с окружающей средой расчеты параметров воздуха выполняются с учетом вида термодинамического процесса, который может быть от изотермического (с полным теплообменом и выполнением условия Т = const) до адиабатического (без теплообмена).
При больших скоростях исполнительных механизмов и течении газа через сопротивления процесс сжатия считается адиабатическим с показателем адиабаты для воздуха k =1,4.
В реальных условиях неизбежно происходит некоторый теплообмен между воздухом и деталями системы и имеет место так называемое политропное изменение состояния воздуха. Весь диапазон реальных процессов описывается уравнениями этого состояния, что позволяет учесть потери, обусловленные трением воздуха, и возможный теплообмен
pV n =const
где р – давление в газе, V =1/ρ - удельный объем, n - показатель политропы, изменяющийся в пределах от n =1 (изотермический процесс) до n =1,4 (адиабатический процесс).
В основу расчетов течения воздуха положено известное уравнение Бернулли движения идеального газа
Слагаемые уравнения выражаются в единицах давления, поэтому их часто называют: z - весовое давление; p - статическое давление; ρ w 2/2 - скоростное или динамическое давление.
На практике часто весовым давлением пренебрегают, и уравнение Бернулли принимает следующий вид
Сумму статического и динамического давлений называют полным давлением p 0. Таким образом, получим
При расчете газовых систем необходимо также иметь в виду, что при расчете движения газов определяется не объемный расход газа, как в гидросистемах, а массовый расход. Это позволяет унифицировать и сравнивать параметры различных элементов пневмосистем по стандартному воздуху (ρ=1,25 кг/м3, ν=14,9 м2/с при p =101,3 кПа и t =20°C).
Следует также учитывать, что при сверхзвуковых скоростях течения воздуха изменяется характер зависимости расхода от перепада давлений на сопротивлении. В связи с этим существуют понятия подкритического и надкритического режимов течения воздуха. Смысл этих терминов рассмотрен ранее.
Применение уравнения Д. Бернулли к расчету движения газа. Уравнение Д. Бернулли для двух сечений потока, отстоящих друг от друга на бесконечно малое расстояние dl можно представить в виде
(15.1)
Пренебрегая влиянием веса газа и изменением скоростей, последнее уравнение (14.1) представим в виде
(15.2)
Так как 
где: ω - площадь поперечного сечения трубы, м2; G - весовой расход газа, н/с; γ - удельный вес, н/м3, выражение (15.2) примет вид
или 
(15.3)
При изотермическом процессе уравнение состояния имеет вид p / γ = const откуда 
С учетом последнего равенства уравнение (15.3) примет окончательный вид
(15.4)
Интегрируя левую часть уравнения (15.4) в пределах от p 1до p 2, а правую - от 0 до L (L - длина трубы) получим
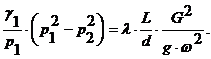(15.5.1)
откуда
(15.5.2)
Формула (15.5) является расчетной формулой для определения весового расхода газа G при заданных перепаде давления (p 1 - p 2) и диаметре трубопровода d. Это же уравнение (15.5) используется и для определения диаметра трубы при заданных значениях G и (p 1- p 2).
Учет перепада давления в трубопроводах. При гидравлическом (аэродинамическом) расчете трубопроводов для газов следует различать два случая:
- движение при малых относительных перепадах давления;
- движение при больших перепадах давления.
При этом под относительным перепадом давления D р/р српонимают отношение абсолютного перепада давления между начальным и конечным сечением D р к среднему давлению на участке р ср = (р 1 +р 2)/2.
При малых относительных перепадах давления (D р/р ср < 5%)можно, пренебрегая сжимаемостью, считать плотность транспортируемого газа неизменной по длине трубопровода; тогда гидравлический (аэродинамический) расчет трубопроводов для газов принципиально не отличается от расчета трубопроводов для несжимаемых жидкостей.
При больших относительных перепадах давления (D р/р ср>5%) пренебрегать сжимаемостью газа нельзя и нужно учитывать уменьшение давления транспортируемого газа по длине трубопровода, сопровождающееся снижением плотности газа с возрастанием его скорости в направлении движения.
3.2. РАСЧЕТ ГАЗОПРОВОДОВ ПРИ МАЛЫХ ПЕРЕПАДАХ ДАВЛЕНИЯ
Особенности расчета течения газа по трубам при малых перепадах давления. При малых перепадах давления уравнение Бернулли для несжимаемой жидкости принимает вид
где D p пот - потерянное давление.
В трубопроводах для газов в большинстве практических случаев слагаемым ρ g (z 1- z 2) в этом уравнении можно пренебречь, так как вследствие очень малой плотности газа его влияние слишком мало по сравнению с другими членами уравнения. Пусть, например, для трубопровода D z = 20м, а давление, развиваемое вентилятором, D р =25 000 Па.
Тогда ρ g D z =1,2 кг/м3.9.81.20 м = 240 Па, что составляет всего 0,01 D р, и, следовательно, членом ρ g D z можно пренебречь.
Перепишем уравнение Бернулли с учетом сказанного выше
а при постоянном сечении трубопровода
(15.6)
т.е. весь перепад давления в трубопроводе обусловлен потерями давления на преодоление гидравлических сопротивлений. Формулу для определения потерь давления на трение представляют следующим образом (Н/м2)
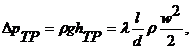(15.7)
а для определения потерь давления в местных сопротивлениях
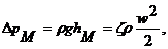(15.8)
где ρ = р ср/(RT) - средняя плотность газа, кг/м3 [здесь р ср = (р 1 + р 2)/2; p 1и р 2- давления в концевых сечениях трубопровода].
Входящий в формулы (15.7) и (15.8) член ρ w 2 /2 называют динамическим давлением.
Формулу (15.7) представляют также в виде
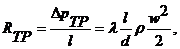(15.9)
где R ТР- удельное сопротивление (сопротивление трения на 1 м длины трубопровода); R ТР связано с гидравлическим уклоном i TР зависимостью R ТР = ρ gi TР, а гидравлический уклон i TР выражается в виде 
.
Особенности гидравлического расчета длинных газопроводов низкого давления. В длинных газопроводах потери давления на местные сопротивления невелики по сравнению с потерями давления на трение, и здесь можно полагать
(15.10)
Подставляя в уравнение (15.10) значение λ = 0,11(k Э / d + 68Re)0,25, получаем, рекомендуемую А.Д. Альтшулем, формулу для определения потерь давления в газопроводах низкого давления
(15.11)
где D р тр - потеря давления, мм. вод. ст.; l - расчетная длина газопровода, м; k Э - эквивалентная шероховатость, см; d - диаметр трубопровода, см; ν - кинематический коэффициент вязкости газа, м2/с; Q - расход газа, м3/ч; у- удельный вес газа, кгс/м3 (при температуре 0°С и давлении 760 мм рт. ст.).
Представляют интерес два частных случая. Если k Э / d << 1922 d v / Q (при движении газа с малыми скоростями в гладких трубах), формула (15.11) упрощается
(15.12)
При обычных условиях расчета газопроводов этой формулой можно пользоваться при скоростях течения газа w <3 м/с.
Если k Э / d >> 1922 d ν / Q (при движении газа с большими скоростями в трубопроводах со значительной шероховатостью), то
В частности, для новых стальных труб при k Э=0,1 мм
Особенности гидравлического расчета вентиляционных воздуховодов. Вентиляционные трубы (каналы) часто имеют прямоугольное или квадратное сечение, поэтому вместо диаметра в уравнение (15.7) вводят эквивалентный диаметр d Э, в результате чего получаем формулу для определения удельного сопротивления в следующем виде
(15.13.1)
Коэффициент гидравлического трения λ вентиляционных воздуховодов определяют по формуле А.Д. Альтшуля, поэтому можно записать
(15.13.2)
При расчетах вентиляции потери давления на местные сопротивления (повороты потока, слияние и деление потока и др.) имеют, как правило, большее значение, чем потери на трение, и их учитывают особо; при этом полезно также учитывать зависимость коэффициентов местных сопротивлений от числа Рейнольдса Re.
3.3. РАСЧЕТ ГАЗОПРОВОДОВ ПРИ БОЛЬШИХ ПЕРЕПАДАХ ДАВЛЕНИЯ
Особенности движения газа при больших перепадах давления. При расчете длинных трубопроводов (имеющих часто длину, равную десяткам и сотням километров), а также трубопроводов сжатого воздуха необходимо учитывать значительные перепады давления между началом и концом трубопровода.
В этом случае нельзя без больших погрешностей полагать плотность газа постоянной по длине трубопровода, как это делается при расчете газопроводов низкого давления.
Кроме того, даже при сохранении постоянства диаметра по длине газопровода движение газа в таких трубопроводах является неравномерным.
Действительно, в соответствии с уравнением неразрывности ρω w = const или pw = const при ω = const. Но давление газа по длине газопровода уменьшается (т. е. уменьшается его плотность), следовательно, возрастает скорость движения газа, которая в конце газопровода всегда выше, чем в его начале.
Далее, при расчетах таких газопроводов можно пренебрегать не только изменениями удельной энергии положения, т.е. членом z 1- z 2в уравнении Бернулли (об этом уже говорилось выше), но также изменениями удельной кинетической энергии газа.
Пусть, например, D р= р 1- р 2 = 196 000 Па (р 1=294 000 Па); D z = z 1- z 2=20 м; w 1=20 м/с; w 2 = 25 м/с; t =27°С=300° К; R =287 Дж/(кг.К). Тогда
Таким образом, перепад давления в 500 раз больше изменения удельной кинетической энергии и в 300 раз больше изменения удельной энергии положения.
Учет термодинамических процессов, протекающих при движении газа по трубопроводу, при больших перепадах давления. При расчетах движения газов с большими перепадами давления уравнение Бернулли сводится к зависимости (для бесконечно малого участка трубопровода, на котором плотность газа и скорость его движения можно считать постоянными)
- dp = dp TР. (15.14.1)
С учетом формулы Дарси - Вейсбаха формула (14.13) получает вид
(15.14.2)
Для интегрирования этого уравнения нужно знать характер изменения скорости, плотности и коэффициента гидравлического трения вдоль газопровода, т. е. зависимости ρ = f (l); w = f 1(l); λ = f 2(l). Эти зависимости определяются термодинамическими процессами, протекающими при движении газа по трубопроводу. Если теплообмен между газом и окружающей средой отсутствует, газ будет расширяться адиабатически, и его температура будет непрерывно понижаться. При наличии теплообмена между газом и окружающей средой температура газа Т может сохраняться постоянной по всей длине газопровода (изотермическое течение), равной температуре окружающей среды. Это обычно наблюдается в длинных трубопроводах без тепловой изоляции, и поэтому большинство промышленных газопроводов работает в условиях изотермического режима.
Как известно, коэффициент гидравлического трения λ = f (Re; k Э / d). Относительная шероховатость по длине газопровода не меняется (для данных k Эи d). Число Рейнольдса можно представить в виде
где G - массовый расход.
Основные зависимости для расчета газопроводов при больших перепадах давления. При изотермическом режиме динамическая вязкость сохраняется неизменной по длине трубопровода (так как температура газа не меняется), а следовательно, остается постоянным и число Рейнольдса. Таким образом, несмотря на изменение средней скорости движения газа и его плотности коэффициент гидравлического трения вдоль газопровода не меняется.
Введем в уравнение (6.52) скорость w 1в начале газопровода. Скорость w и плотность ρ в любом сечении газопровода связаны со скоростью и плотностью в начальном сечении w 1 и ρ1 уравнением неразрывности w = w 1ρ1 / p. Подставляя это выражение в уравнение (15.14), получим
(15.15)
С другой стороны, из уравнения состояния газа имеем
(15.16)
в соответствие с чем формулу (15.15) можно привести к виду
(15.17)
Интегрируя это уравнение от р 1до р 2(p 2 - давление в конце рассматриваемого участка газопровода), получим
откуда
(15.18)
Уравнение (15.18) можно представить также в виде
(15.19)
Левая часть последнего уравнения может быть преобразована
поэтому
(15.20)
Так как 
то, подставляя последнее выражение в уравнение (15.18), получим окончательно
(15.21)
Уравнение (15.21) отличается от формулы Дарси - Вейсбаха для определения потерь давления при движении несжимаемой жидкости лишь множителем, зависящим от отношения D p / p 1. До тех пор, пока сохраняется условие
D p / p 1 < 5%, (14.22)
пренебрежение этим множителем дает ошибку около 2,5%, что допустимо в большинстве инженерных расчетов.
Таким образом, можно прийти к выводу, что не абсолютная величина начального давления газа р 1определяет, можно ли при расчете газопровода пользоваться формулой Дарси - Вейсбаха, а относительная величина изменения этого давления по длине газопровода в целом.
Определения весового расхода газа при расчете газопроводов при больших перепадах давления. Формула для определения весового расхода газа, как отмечалось выше, имеет вид
(15.23)
При турбулентном режиме, подставив в уравнение (14.18) значение λ= 0,11(k Э / d + 68Re)0,25 (см. 8.2.2), и приведя к нормальным условиям (температура 0°С и давление 0,1 МПа), получаем, рекомендуемую А.Д. Альтшулем, формулу
(15.24)
где p 1 и p 2 - абсолютное давление газа вначале и в конце газопровода, ат; L – длина газопровода, км; d - диаметр газопровода, см; k Э - эквивалентная шероховатость, см; γ- удельный вес газа, кгс/см3; Q - расход газа, м3/ч; ν - кинематическая вязкость газа, м2/с.
Значения γ, Q и ν приводятся к нормальным условиям. Уравнение (15.24) представляет собой обобщенную формулу, действительную во всей области турбулентного режима.
Для случаев, когда k Э / d << 1922 d ν / Q и k Э / d >> 1922 d ν / Q, уравнение (15.24) получает соответственно вид
(15.25)
(15.26)
Формула (15.26), действительная для квадратичной области сопротивления, применяется при больших скоростях газа (w >50 м/с).
Определения диаметра трубопровода при расчете газопроводов при больших перепадах давления. В практических расчетах для определения коэффициент трения l часто используют формулы, полученные на основании обработки опытных данных по перекачке газов по трубам. Так, для определения lв квадратичной области турбулентного режима для стальных трубопроводов используют формулу
(15.27)
где d выражается в м.
Для определения l резиновых шлангов пользуются формулой
(15.28)
где d - в метрах.
Подставив выражения для коэффициента трения l из (15.27) и (15.28) в формулу (15.23) и разрешив ее относительно диаметра трубы (шланга) d, получим формулы для определения требуемого диаметра при заданном весовом расходе воздуха G (и остальных исходных данных):
для стальных труб 
(15.29)
для резиновых шлангов 
(15.30)
Ответ по формулам (15.29) и (15.30) получается в м.
3.4. ОСОБЕННОСТИ РАСЧЕТА ПАРОПРОВОДОВ
Особенности работы паропроводов. Паропровод - трубопровод для транспортировки пара. Применяется на предприятиях, использующих пар в качестве технологического продукта или энергоносителя.
Трассировка паропроводов производится с учетом минимизации потерь энергии из-за аэродинамического сопротивления парового тракта.
При проектировании обычных паропроводов, как правило, назначают возможно меньший диаметр трубы для уменьшения тепловых потерь. При этом получаются сравнительно высокие скорости движения пара (от 10 до 60 м/с), вследствие чего даже в коротких паропроводах возникают значительные потери напора.
При перекачивании перегретых паров трубопроводы самым тщательным образом изолируют, и их тепловые потери незначительны, но все же характер изменения состояния перегретого пара в результате устранения теплообмена между потоком и наружной средой уже не является изотермическим. Не будет он и строго адиабатическим - даже в хорошо изолированной трубе условия будут отличаться от условий при обратимом адиабатическом изменении объема, так как турбулентность, возникающая при движении, переходит частично в тепло, которое изменяет уравнение энергии (энергия, переходящая в потери, возвращается в виде механической энергии).
Таким образом, с одной стороны, температура пара имеет тенденцию к снижению по длине трубопровода в результате расширения пара, с другой стороны, - к возрастанию вследствие поступления тепла от потерь напора.
В результате режим движения пара находится между изотермическим и адиабатическим процессами.
Поскольку температура пара меняется по длине паропровода, меняются также динамическая вязкость μ, число Рейнольдса Rе и в общем случае коэффициент гидравлического трения λ.Однако вследствие значительных скоростей движения пара (десятки метров в 1 с) сопротивление относится чаще всего к квадратичной области, где λ от Re не зависит.
В паропроводах низкого давления (например, в отопительных системах) плотность пара и его температура в процессе движения изменяются так мало, что расчеты можно производить по формулам для несжимаемых жидкостей.
Основные сведения о паропроводах и конденсатопроводах систем парового отопления низкого давления. В отличие от системы водяного отопления трубопровод системы парового отопления разделяется на паропровод и конденсатопровод, но методы расчета обеих систем аналогичны.
Давление пара в котле принимают в зависимости от протяженности паропровода, соединяющего котел с наиболее удаленным нагревательным прибором. Более высокие давления пара, равные 70 кПа и более, принимают при теплоснабжении группы зданий от одной котельной.
Располагаемым давлением на преодоление сопротивлений трения и местных сопротивлений в паропроводе системы отопления является разность давлений пара в котле (или в тепловом пункте после редуктора) и перед вентилем наиболее удаленного прибора от котла (от теплового пункта).
На преодоление сопротивлений вентиля и отопительного прибора в системах низкого давления при самотечном конденсатопроводе оставляют давление не менее 1500 Па, обычно 2000 Па.
В системе парового отопления низкого давления потери давления на трение принимают в размере 5%, а на местные сопротивления - 35% (меньше, чем в системах водяного отопления) полной потери давления.
Потери давления на преодоление местных сопротивлений подсчитывают по таблице, составленной для парового отопления низкого давления, или по номограмме. Величины коэффициентов местного сопротивления в системах парового отопления принимают те же, что и в системах водяного отопления.
Суммарные потери давления (на трение и местные сопротивления) по отдельным веткам паропровода системы отопления, не должны разниться более чем на 25%.
Диаметры конденсатопроводов обычно определяют по таблицам в зависимости от их длины, количества тепла, выделяемого паром при конденсации, и вида конденсатопровода (сухой, мокрый, вертикальный, горизонтальный).
По величине потерь и по тепловой нагрузке участков, как и при расчете систем водяного отопления, подбирают диаметры паропроводов, пользуясь расчетной таблицей или номограммой.
Таким образом, гидравлический расчет системы парового отопления низкого давления имеет ту особенность, что паропроводы и конденсатопроводы рассчитываются отдельно и не составляют одного общего расчетного кольца, как при гидравлическом расчете систем водяного отопления.
Для обеспечения бесшумной работы системы и предотвращения гидравлических ударов, которые могут привести к повреждению паропроводов, скорости движения пара в них при попутном движении пара и конденсата не должны превышать при низком давлении 30 м/с, а при встречном движении пара и конденсата соответственно 20 м/с.
Основные сведения о паропроводах и конденсатопроводах систем парового отопления высокого давления. Расчет паропроводов систем повышенного и высокого давления проводят с учетом изменения объема пара при изменении его давления и уменьшения расхода пара вследствие попутной конденсации.
В случае, когда известно начальное давление пара р п и задано конечное давление перед отопительными приборами р пр, расчет паропроводов выполняют до расчета конденсатопроводов.
Гидравлический расчет выполняют по способу эквивалентных длин, который применяется, когда линейные потери давления являются основными, а потери давления в местных сопротивлениях сравнительно малы.
Действительная скорость пара не должна превышать 80 м/с (30 м/с в системе повышенного давления) при движении пара и попутного конденсата в одном и том же направлении; 60 м/с (20 м/с в системе повышенного давления) при встречном их движении.
Итак, гидравлический расчет проводится с усреднением значений плотности пара на каждом участке, а не в целом для системы, как это делается при гидравлических расчетах систем водяного отопления и парового отопления низкого давления.
Потери давления в местных сопротивлениях, составляющие всего около 20 % общих потерь, определяют через эквивалентные им потери давления по длине труб.
Для преодоления сопротивлений, не учтенных при расчете по основным направлениям, оставляют запас не менее 10 % расчетного перепада давлений.
При увязке потерь давления в параллельно соединенных участках допустима невязка до 15%.
Для систем высокого давления в большинстве случаев гидравлический расчет паропроводов выполняют после расчета конденсатопроводов, в результате которого определяется давление перед отопительными приборами р Пр.
Далее, если известно начальное давление пара р, давление для паропроводов определяют, как описано выше. Если же давление р не задано, то его находят, проводя расчет по предельно допустимой скорости движения пара.
Точный расчет паропровода системы высокого давления производят по номограмме и таблицам, составленным с учетом изменения плотности (объемной массы) пара.
Потери давления в местных сопротивлениях определяют методом замены их эквивалентной длиной, представляющей собой длину трубопровода данного диаметра, на которой потеря из трещин равна потере в местном сопротивлении при коэффициенте 1. Потеря давления на местные сопротивления в долях общей величины сопротивления трубопровода в системах парового отопления высокого давления составляет 20-25%.
Расчет паропроводов и конденсатопроводов систем парового отопления. В общем случае расчет паропроводов ведется в соответствие с требованиями СНиП. Так, расчет трубопроводов систем парового отопления осуществляется в соответствие с требованиями СНиП 2.04.07-86 «Тепловые сети».
Диаметры трубопроводов паровых систем отопления рассчитывают отдельно для паропроводов и конденсатопроводов. Диаметры паропроводов низкого давления определяют так же, как в системах водяного отопления.
Потери давления в главном циркуляционном кольце системы Δ р рк, Па, представляют собой сумму сопротивлений (потерь давления) всех участков, входящих в это кольцо
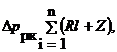(15.31)
где R - удельная потеря давления на трение по длине кольца (потеря давления, приходящаяся на один погонный метр кольца), Па/м; l - длина участка главного кольца, м; Z - потери давления на преодоление местных сопротивлений участка, Па.
Задаваясь значением Δ р рк, определяют удельную потерю давления на трение по формуле
(15.32)
где n - доля потери давления на трение от общих потерь в кольце; Σ l - суммарная длина участков главного циркуляционного кольца, м.
Затем определяют требуемое давление пара в котле р к, которое должно обеспечивать преодоление потерь давления в главном циркуляционном кольце. В системах парового отопления низкого давления разность давлений пара в котле и перед нагревательными приборами расходуется только на преодоление сопротивлений паровой магистрали, а конденсат возвращается самотеком. Для преодоления сопротивления отопительных приборов предусматривают запас давления р пр = 2000 Па.
Удельную потерю давления пара можно определить по формуле
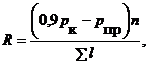(15.33)
где 0,9 - значение коэффициента, учитывающего запас давления на преодоление неучтенных сопротивлений.
Для систем парового отопления низкого давления долю потерь на трение n принимают 0,65, а для систем высокого давления - 0,8. Вычисленное по формуле (15.33) значение удельной потери давления должно равняться или быть несколько больше значения, определенного по формуле (15.32).
Диаметры паропроводов определяют с учетом вычисленных удельных потерь давления и тепловой нагрузки каждого расчетного участка.
Диаметры паропроводов можно также определять, используя специальные таблицы в справочниках или номограмму (рис. 15.1), составленную для средних значений плотности пара низкого давления.
При конструировании систем парового отопления скорость пара в паропроводах следует принимать с учетом рекомендаций, приведенных в табл. 15.1. В остальном методика гидравлического расчета паропроводов низкого давления и сопротивлений циркуляционных колец полностью аналогична расчету трубопроводов водяных систем отопления.
Рис. 15.1. Номограмма для расчета диаметров паропроводов и самотечных конденсатопроводов
Таблица 15.1
Скорости пара в паропроводах
| Давление пара, кПа | Направление движения пара и конденсата | Предельная скорость пара, м/с |
| 70 и менее | Попутное | 30 |
| Встречное | 20 | |
| Более 70 | Попутное | 80 |
| встречное | 60 |
3.5. ДВИЖЕНИЕ НЕОДНОРОДНЫХ (ДВУХФАЗНЫХ) ЖИДКОСТЕЙ В ТРУБАХ
