Как уже говорилось раньше, при изучении физических свойств жидкостей вязкость существенно зависит от температуры жидкости и почти не зависит от плотности и давления. При этом коэффициент динамической вязкости m и коэффициент кинематической вязкости n у капельных жидкостей с ростом температуры уменьшаются, а у газов возрастают.
Общее уравнение энергии в интегральной форме.
Три уравнения сохранения для газов – количества движения, массы и энергии, в интегральной форме могут быть записаны следующим образом
причем в первом случае
во втором
в третьем
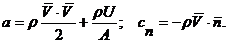
В приведенных равенствах: – (τ) – произвольный объем жидкости, ограниченный покерхностью (S), 
- единичный вектор внешней нормали к (S), t1 и t2 - два каких-то момента времени, p – давление, ρ – плотность, 
- скорость (вектор), U – внутренняя энергия единицы массы в какой-либо точке объема (τ) или поверхности (S).
Общее уравнение энергии в дифференциальной форме.
Для той части жидкости, в которой гидродинамические элементы и их первые производные непрерывны, можно написать уравнения в дифференциальной форме:
уравнение движения (приращение количества движения частицы жидкости равно импульсу силы)
уравнение неразрывности (сохранения массы)
уравнение энергии (условие адиабатичности)
Здесь k – отношение теплоемкостей Cp/Cv. Для воздуха k = 1,4.
Уравнение Д.Бернулли для газов
При установившемся одномерном плавноизменяющемся адиабатичесеком движении газа, как и для несжимаемой жидкости, можно поток разбить на элементарные струйки. При этом живые сечения потока можно считать плоскими. Для такого потока газа будут справедливы:
уравнение Д.Бернулли в интегральной форме: вдоль потока
уравнение Д.Бернулли в дифференциальной форме
уравнение неразрывности (постоянства массы)
В последних равенствах w – средняя скорость течения в живом сечении потока.
Число Маха
Многие свойства потока сжимаемой жидкости и характер взаимодействия его с окружающей средой зависят от соотношения скорости движения потока и скорости звука в нем. Учитывая важность этого обстоятельства, в гидродинамике сжимаемой жидкости рассматриваются два вида одномерного движения потоков:
- дозвуковое течение, когда скорость движения потока меньше скорости звука; и
- сверхзвуковое течение, когда скорость движения потока превосходит скорость звука в нем.
Сжимаемость жидкости часто характеризуют безразмерной величиной, равной отношению скорости потока сжимаемой жидкости w к скорости звука в нем a. Это отношение называют числом Маха или числом М:
Если M < 1 - поток считается дозвуковым,
М > 1- сверхзвуковым.
