Уравнение Бернулли для потока реальной жидкости

Распространим уравнение Бернулли на поток жидкости при установившемся плавно изменяющемся движении. Предварительно нужно рассмотреть, какое выражение получат удельная потенциальная и удельная кинетическая энергия потока, если принимать во внимание действительное распределение давлений и скоростей, свойственных движущейся жидкости. Остановимся вначале на удельной потенциальной энергии потока. В соответствии со свойствами плавноизменяющегося движения гидродинамическое давление в плоскости живого сечения распределяется по гидростатическому закону. Поясним это на примере потока жидкости в открытом русле (канале), продольный профиль которого представлен на рис.3 –1.

В сечении 1-1 выберем произвольную точку n, находящуюся на расстоянии z_n от плоскости сравнения O - O. Если в эту точку потока опустить пьезометрическую трубку, то уровень воды в ней поднимется на величину до уровня свободной поверхности жидкости, являющейся в данном случае пьезометрической линией.

Таким образом, для точки " n " удельная потенциальная энергия выражается следующим образом

Для какой-то другой точки " m " в том же живом сечении 1-1 выражение удельной потенциальной энергии будет иметь вид

Из рис. 3 – 1 видно, что

т.е. сумма высот положения (z) и давления для этих, а также и для всех других точек данного живогосечения является величиной постоянной.

Отсюда следует, что удельная потенциальная энергия не зависит от положения рассматриваемой точки в плоскости живого сечения и для данного живого сечения, будучи вычис-лена относительно какой-либо плоскости сравнения O - O, является величиной постоянной

(3 – 1)

Сравнивая уравнения (1– 11) и (3 – 1) замечаем, что выражение удельной потенциальной энергии установившегося потока жидкости при плавно изменяющемся движении имеет такой же вид, как и выражение потенциальной энергии в уравнении Бернулли для элементарной струйки реальной жидкости.

Сложнее обстоит дело с выражением удельной кинетической энергии потока жидкости. Величина удельной кинетической энергии в уравнении Бернулли для элементарной струйки, как мы убедились, выражается членом 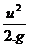, где u - скорость движения частиц в струйке. Ввиду сложности действительного распределения скоростей по сечению мы ввели понятие средней скорости потока v, исходя из принципа сохранения одного и того же расхода Q. Однако при такой предпосылке удельная кинетическая энергия потока, вычисленная в данном живом сечении по средней скорости v - 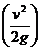будет отличаться от кинетической энергии, учитывающей действительное распределение скоростей по сечению. Пусть поток состоит из n элементарных струек, имеющих в данном живом сечении скорости u₁, u₂, u₃., …, u_n. Тогда среднее значение удельной кинетической энергии всего потока по сечению будет равно

> .

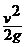Это объясняется тем, что квадрат средней величины всегда меньше среднего значения квадратов этих величин. Таким образом, вычисляя удельную кинетическую энергию потока по средней скорости , мы допускаем занижение ее величины по сравнению с действительной кинетической энергией. Это можно учесть введением поправочного коэффициента a, большего единицы, к третьему члену уравнения Бернулли, который может быть теперь записан в следующем виде

. (3 – 2)

Последнее выражение представляет собой запас удельной кинетической энергии потока жидкости при плавно изменяющемся движении, где v - средняя скорость потока;

a - коэффициент, характеризующий отношение действительной кинетической энергии потока к кинетической энергии его, вычисленной по средней скорости, и называемый коэффициентом неравномерности распределения скоростей по живому сечению или коррективом скорости.

Выполненными исследованиями установлено, что среднее значение коэффициента a для установившегося плавно изменяющегося движения в реках, каналах и трубах составляет a @ 1,03 … 1,10.

Во многих практических случаях гидравлических расчетов (например, при расчете труб) этим небольшим отличием коэффициента a от единицы пренебрегают, принимая a = 1,0.

Учитывая сказанное выше относительно удельной потенциальной и кинетической энергии потока можно записать, что удельная энергия потока в данном живом сечении

Тогда для двух различных сечений потока при установившемся плавно изменяющемся движении уравнение Бернулли примет следующий вид (рис. 3.2):

(3 – 3)

В уравнении (3 – 3):

z₁ – расстояние от произвольно выбранной точки в живом сечении w₁ до плоскости сравнения О - О;

p₁ – гидродинамическое давление, определенное в той же точке живого сечения потока;

g - удельный вес жидкости;

v₁ - средняя скорость в живом сечении w ₁;

g - ускорение силы тяжести;

a ₁ - коэффициент неравномерности распределения скоростей в живом сечении w ₁;

z₂, p₂, v₂, a₂ - те же величины, определенные в живом сечении w ₂.

h_w - удельная энергия (потеря напора), затраченная на преодоление гидравлических сопротивлений в пути между первым к вторым сечением.

Из уравнения Бернулли для потока реальной жидкости следует, что удельная энергия уменьшается по длине потока в направлении движения, так как часть энергии затрачивается на преодоление гидравлических сопротивлений в пределах данного участка потока. Определению потерь напора на преодоление гидравлических сопротивлений посвящен следующая тема.