Рассмотрим особенности потоков с до- и сверхзвуковыми скоростями движения (течения).
Для установления указанных зависимостей воспользуемся уравнением Д.Бернулли для одномерного изоэнтропического движения потока идеального газа, записанного в виде

Если учесть, что скорость звука в идеальном газе равна
 ,
,
то уравнение примет вид

Из последнего уравнения видно, что скорость звука a в газовом потоке связана со скоростью течения потока газа w. При скорости течения газа w = 0 (газ находятся в покое - в заторможенном состоянии) скорость звука в нем имеет наибольшее значение:

где р o и r o - соответственно, абсолютное давление и плотность газа, находящегося в покое (в заторможенном состоянии).
Скорость ao называют скоростью звука при торможении.
Уравнение Бернулли теперь можно записать в виде:
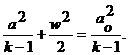
С увеличением скорости потока w скорость звука, как это следует из последнего уравнения, уменьшается и в некотором сечении потока они могут оказаться равными.
Скорость потока, равная местной скорости звука в нем, называется критической и обозначается wкр. Скорость звука в этом случае также называется критической и обозначается aкр. Уравнение Бернулли принимает вид:

Используя уравнения можно установить связь между скоростью звука при торможении ao и критической скоростью звука aкр. Приравняв правые части двух предыдущих уравнений, получим:

откуда

При очень большой скорости течения потока w скорость звука, как это видно из уравнения Бернулли, может обратиться в нуль. Это может быть тогда, как это следует из формулы для скорости звука (см. стр.),когда абсолютная температура газа Т будет равна нулю. Скорость газового потока в этом случае называют максимальной wмакс или предельной wпред. Уравнение Бернулли в этом случае примет вид:

На основании вышеизложенного уравнение Д.Бернулли можно представить так:
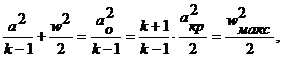
откуда

Т.о. если критическая скорость звука aкр примерно на 10% меньше скорости звука ao в покоящемся воздухе при атмосферном давлении, то максимальная скорость течения его wмакс (при истечении в пустоту) более чем в два раза превышает ao.
Для установления подобных же зависимостей для одномерного изоэнтропического движения потока воды надо воспользоваться уравнением Д.Бернулли:

и учесть что скорость звука в воде равна

Получим:

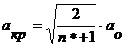 ;
;

Изложенное свидетельствует о тесной зависимости между скоростью звука и скоростью течения сжимаемых жидкостей, и это обстоятельство широко используется при производстве расчетов.






