Потери напора от местных сопротивлений обусловлены резкими изменениями величины и направления скорости движения жидкости. Простейшие местные гидравлические сопротивления можно разделить на расширения, сужения и повороты русла, каждое из которых может быть внезапным или постепенным. Они определяются по формуле Дарси-Вейсбаха
, (3.2.2)
где zм.с. – коэффициент местного сопротивления;
- скоростной напор в сечении за местным сопротивлением.
Значение коэффициента zм.с. обычно определяют экспериментально и лишь в некоторых случаях теоретически.
ДВИЖЕНИЕ НЕСЖИМАЕМОЙ ЖИДКОСТИ В НАПОРНЫХ ТРУБОПРОВОДАХ
2.1. ПРИМЕНЕНИЕ УРАВНЕНИЯ БЕРНУЛЛИ И ПРИНЦИПА СЛОЖЕНИЯ ПОТЕРЬ НАПОРА К РАСЧЕТУ КОРОТКИХ ВОДОПРОВОДНЫХ ТРУБ
Расчет коротких водопроводных труб
Короткими, в гидравлическом смысле, трубами называются трубы, в которых потери напора от местных сопротивлений получаются или одного порядка с потерями на трение по длине, или даже превышают последние.
Рассмотрим схему трубопроводов – два отрезка труб диаметром d1 и d2 и три местных сопротивления – вход из резервуара в трубу, внезапное сужение трубы (d1 > d 2) и вентиль в конце второго отрезка трубы (рис. 3.4).
Примем, что плоскость сравнения проходит через ось трубы, первое сечение – на уровне поверхности воды в резервуаре, второе – непосредственно на выходе из трубы.
Напишем уравнение Бернулли в общем виде:
,
где
.
Примем a1 = a2 = 1.
Рис. 3.4
При выбранных сечениях и плоскости сравнения будем иметь:
Уравнение Бернулли принимает вид:
.
Вынеся в правой части последнего равенства множитель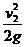 
за скобки, получим
. (3.3)
Квадратный корень из суммы в скобках обозначают m и называют коэффициентом расхода системы:
.
Из уравнения неразрывности для потока жидкости следует:
.
С учетом последнего равенства окончательное выражение для коэффициента расхода системы запишем в виде
. (3.4)
С учетом введенного коэффициента расхода системы m уравнение Бернулли (3.3) принимает вид
,
откуда
.
Опуская индекс 2 в обозначении скорости жидкости и площади сечения трубы на выходе из системы (в нашем примере v = v2 , w = w2), получим следующие выражения для скорости жидкости v и расхода Q = w. v на выходе из системы
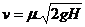. (3.5)
. (3.6)
Для идеальной жидкости все коэффициенты сопротивления z равны нулю, и коэффициент расхода m = 1, а при вязкой всегда m < 1, поэтому физический смысл коэффициента расхода системы можно сформулировать следующим образом: коэффициент расхода системы m показывает во сколько раз расход нормальной (вязкой) жидкости меньше расхода идеальной жидкости.
