Гидродинамикой сжимаемой жидкости называется раздел механики жидкости, изучающий основные законы движения сжимаемых жидкостей при больших перепадах давления и больших скоростях, причем масштабом скорости является скорость звука в жидкости. При изучении движения следует учитывать изменение её состояния - давления, плотности, температуры, т.е. должны использоваться законы термодинамики.
Гидродинамику сжимаемой жидкости называют газодинамикой (рассматриваются газы) или аэрогидродинамикой, если рассматриваются игазы и жидкости.
Течение газов (сжимаемых жидкостей) рассматривается с учетом ряда условий. Принимается, что газ лишен вязкости или влияние вязкости настолько мало, что им можно пренебречь. К массе газа не подводится тепло из окружающей среды и отсутствует обмен механической энергией. Поэтому процессы, сопутствующие течению газа, являются адиабатическими. Кроме того, в живых сечения потока распределение давления и скоростей течения принимается равномерным. Такая постановка задачи о течении газа называется одномерной.
Как было отмечено в начале курса, сжимаемость жидкости и газов характеризуется модулем упругости Е.
Изменение объема жидкости при изменении давления на D p равно
При т.н. стандартных условиях - температура T = 373 + 15 = 288 ° K и давление p = 1,0332 кгс/см2 = 10332 кгс/м2 = 101325 н/м2 =760 мм рт. ст. модуль упругости воздуха равен - Eвозд = 1,45 кгс/см2, для воды Eвод = 21000 кгс/см2.
Сжимаемость сплошной среды можно также характеризовать отношением приращения давления dp к приращению ее плотности d r. Это отношение равно квадрату скорости распространения звука в среде a2:
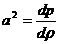или 
Характерной особенностью изучения сжимаемых жидкостей является необходимость учитывать соотношение между давлением p, плотностью (объемным весом) g = g r, удельным объемом 
и температурой T °К (Кельвина). Это соотношение называется уравнением состояния.
Для идеального газа уравнение состояния (уравнение Менделеева –Клайперона):
или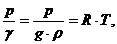 
где: R = 29,27 м/°К - газовая постоянная;
g = 9,81 м/c2 - ускорение силы тяжести.
Для воды при давлении p £ 25000 кгс/см2 уравнение состояния выражается уравнением Тэта:
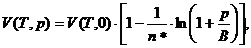
где B и n * приближенно можно считать постоянными: B = 3045 кгс/см2, n * = 7,15.
Далее мы будем рассматривать быстропротекающие процессы, которые с большой точностью можно считать протекающими без обмена теплом, как с внешней средой так и между частями газа (жидкости) внутри, т.е. адиабатическими или изоэнтропическими (эти понятия совпадают для идеального газа), когда dS = 0.
Для газа уравнение состояния при изоэнтропических процессах
где 
- отношение теплоемкостей при постоянном давлении (cp) и при постоянном объеме (cv).
Для воды уравнение изоэнтропы, вытекающее из приведённого выше уравнения состояния, имеет вид:
или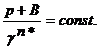 
С учетом приведенных уравнений изоэнтропы имеем:
- для воздуха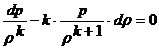 
, или 
- для воды 
или 
Т.о. скорость звука равна:
- в воздухе 
- в воде 
При стандартных условиях: p = 1,0332.104 кгс/м2, плотность воздуха
r = g/ g = 1,23 кгс/м3: 9,81 м/с2 = 0,125 кгс.с2/м4, k = 1,4,
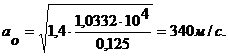
Плотность воды r = 1000/9,81 = 102 кгс.с2/м4, n* = 7,15, B = 3045 кгс/см2,
