Геометрический смысл уравнения Бернулли

Пользуясь методом размерностей нетрудно показать, что все члены уравнения Бернулли имеют размерность длины. Действительно:    

z = [ L];

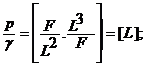
где: T - символ времени; L - символ длины; F - символ силы.

Поэтому все члены уравнения Вернулли можно будет представить себе как высоты.

Условимся, отсчет высот производить от некоторой горизонтальной плоскости координат xOy, которую в дальнейшем будем называть плоскостью сравнения, а след пересечения ее с плоскостью чертежа, представляющий собой горизонтальную линию, обозначим через O – O (рис. 2 – 1).

Координата z измеряет высоту расположения частицы жидкости над плоскостью сравнения и называется высотой положения.

Второй член уравнения -  представляет собой высоту столба жидкости, на которую может подняться уровень жидкости в открытой пьезометрической трубке 1, помещенной в данную точку элементарной струйки, под действием гидродинамического давления в этой точке. Поэтому член   называют пьезометрической высотой или высотой давления.

Для выяснения смысла третьего члена уравнения - величины   в ту же точку A элементарной струйки поместим изогнутую под прямым углом трубку II, открытую с обеих сторон, которую назовем скоростной трубкой. Отверстие нижнего колена этой трубки направим строго против скорости движения частиц в струйке. Под влиянием скорости u_A уровень жидкости в трубке II поднимется выше, чем в пьезометрической трубке 1 на некоторую высоту h, которую мы определим из cледующих соображений.

Избыточный (сверх высоты ) высотой h должен вызывать, согласно закону Торичелли, истечение жидкости из скоростной трубки II со скоростью .

С другой стороны, частицы жидкости, движущиеся в струйке, стремятся войти в отверстие скоростной трубки со скоростью u_A. Так как фактически жидкость не входит в трубку и не вытекает из нее, то  u_A 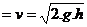          , откуда  .

Следовательно разность высот жидкости в скоростной и пьезо­метрической трубках и выражает собой третий член в уравнении Бернулли. Поэтому член    принято называть скоростной высотой или скоростным напором.

Такова геометрическая интерпретация отдельных членов, входящих в уравнение Бернулли. Применим этот метод геометрического представления к двум сечениям элементарной струйки 1-1 и 2-2.

Площади живых сечений соответственно равны d w₁ и d w₂; скорости движения частиц в этих сечениях u₁ и u₂ в соответствии с (1 – 4) обратно пропорциональны площадям живых сечений. Выберем произвольные точки в сечениях 1-1 и 2-2 (в нашем случае они совпадают с центрами тяжести живых сечений d w₁  и d w₂).           Расстояние от этих точек до плоскости сравнения О-О, соответственно, обозначим через z₁ и z₂.

 Сумма высот положения и давления  называется пьезометрическим напором, а линия p- p, соединяющая вершины пьезометрических напоров, называется пьезометрической линией. Сумма пьезометрического и скоростного напоров, представляющая собой сумму трех членов.уравнения Бернулли, называется полным напором H.

Геометрическое место вершин сумм трех высот: положения, давления и скоростной называется напорной линией N - N. Из уравнения (1 – 8) видно, что для двух произвольно выбранных сечений элементарной струйки 1-1 и 2-2 эта сумма высот есть величина постоянная. Т.е. напорная линия N - N лежит в горизонтальной плоскости, параллельной плоскости сравнения О - О, на рас­стоянии H от нее.

Отсюда геометрический смысл уравнения Вернулли (1 – 8) можно сформулировать следующим образом: для элементарной струйки идеальной жидкости сумма трех высот: геометрической, пьезометрической и скоростной (т.е. полный напор) не изменяется по длине струйки.