Для вывода уравнения Бернулли воспользуемся уравнениями Л.Эйлера применительно к установившемуся движению идеальной жидкости в элементарной струйке. В этом случае гидродинамическое давление не зависит от времени, а является только функцией координат; жидкость принимается несжимаемой, т.е. обладает постоянной плотностью.
Помимо этого примем следующие дополнительные условия:
1) из всех массовых сил действует только сила тяжести;
2) прямоугольная система координат расположена таким образом, что координатная плоскость xOy горизонтальна, а ось Oz направлена вертикально вверх.
Установим связь между перемещением частицы жидкости по элементарной струйке и скоростью ее движения (рис. 1 – 3).
Если частица жидкости "а" в момент времени t находившаяся в плоcкости живого сечения d w за время dt переместится в положение a¢, то путь ее dl= u. dt, где u - скорость движения частицыв элементарной струйке. Обоэначив проекции скорости на координатные оси через ux, uy, uz, а проекции пути dl через dx, dy, dz, можно получить, что
dx = ux.dt;
dy = uy.dt; (2 – 1)
dz = uz. dt.
Эти уравнения накладывают определенные условия на выбор приращения координат dx, dy, dz, которые здесь в отличив от гидростатики не являются произвольными, а представляют собой проекции бесконечно малого пути dl, пройденного частицей. Это обстоятельство сказывается и на окончательном результате интегрирования: полученное уравнение Бернулли будет применимо только для точек одной и той же элементарной струйки.
Для вывода уравнения Бернулли преобразуем и проинтегрируем систему дифференциальных уравнений Эйлера движения жидкости.
Умножая левые и правые части этих уравнений на соответствующие бесконечно малые приращения координат dx, dy, dz и почленно складывая их получим:
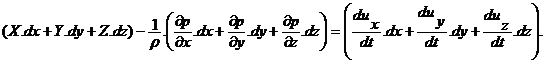(2.2)
Рассмотрим отдельно слагаемые последнего уравнения. При выбранном направлении осей координат проекции единичной массовой силы (в данном случае силы тяжести) примут следующие значения
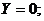
Поэтому первый трехчлен в уравнении (1 – 6) преобразуется к виду
.
Второй трехчлен при принятом условии независимости гидродинамического давления от времени представляет собой полный дифференциал гидродинамического давления dp:
Трехчлен в правой части уравнения (1 – 6) преобразуем с учетом выражений (В – 1) и (1 – 5) следующим образом:
= 
Подставляя найденные выражения слагаемых в уравнение (2 – 2) и, перенося все члены в левую часть, будем иметь:
Разделив все члены последнего уравнения на g, мы тем самым отнесем их к единице веса движущейся жидкости (т.к. исходные уравнения Эйлера относились к единице массы жидкости, а mg= G).
В результате почленного деления, учитывая, что r. g= g, получим:
,
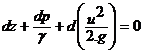откуда
.
Интегрируя это дифференциальное уравнение в полных дифференциалах, получим следующее выражение
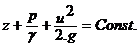(вдоль струйки) (2 – 3)
Уравнение Даниила Бернулли, полученное в 1738 г., является фундаментальным уравнением гидродинамики.
Уравнение Бернулли дает связь между давлением p, средней скоростью υ и пьезометрической высотой z в любой фиксированной точке элементарной струйки при установившемся движении жидкости и выражает закон сохранения энергии движущейся жидкости.
Запишем уравнение Бернулли применительно к двум любым произвольно выбранным сечениям для идеальной жидкости.
Рассмотрим трубопровод переменного диаметра, расположенный в пространстве под углом β (рис.3.5).
Рис.3.5. Схема к выводу уравнения Бернулли для идеальной жидкости
Выберем произвольно на рассматриваемом участке трубопровода два сечения: сечение 1-1 и сечение 2-2. Вверх по трубопроводу от первого сечения ко второму движется жидкость, расход которой равен Q.
Для измерения давления жидкости применяют пьезометры - тонкостенные стеклянные трубки, в которых жидкость поднимается на высоту p/ρg.
В каждом сечении установлены пьезометры, в которых уровень жидкости поднимается на разные высоты.
Кроме пьезометров в каждом сечении 1-1 и 2-2 установлена трубка, загнутый конец которой направлен навстречу потоку жидкости, которая называется трубка Пито.
Жидкость в трубках Пито также поднимается на разные уровни, если отсчитывать их от пьезометрической линии.
Пьезометрическую линию можно построить следующим образом. Если между сечением 1-1 и 2-2 поставить несколько таких же пьезометров и через показания уровней жидкости в них провести кривую, то мы получим ломаную линию (рис.3.5).
Однако высота уровней в трубках Пито относительно произвольной горизонтальной прямой 0-0, называемой плоскостью сравнения, будет одинакова.
Если через показания уровней жидкости в трубках Пито провести линию, то она будет горизонтальна, и будет отражать уровень полной энергии трубопровода.
Для двух произвольных сечений 1-1 и 2-2 потока идеальной жидкости уравнение Бернулли имеет следующий вид:
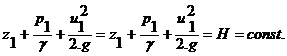
Так как сечения 1-1 и 2-2 взяты произвольно, то полученное уравнение можно переписать иначе:
Таким образом, сумма трех членов уравнения Бернулли для любого сечения потока идеальной жидкости есть величина постоянная.
Для уяснения смысла отдельных членов, входящих в уравнение Бернулли, рассмотрим их с геометрической и энергетической точки зрения.
