К недопустимости текущего оптимального решения может привести как изменение правых частей ограничений (т.е. изменение элементов вектора b), так и введение во множество ограничений задачи нового ограничения. В любом случае недопустимость решения проявится в том, что, по крайней мере, один элемент в векторе В-1b станет отрицательным, т.е. одна или несколько базисных переменных примут отрицательное значение.
Изменение элементов вектора b правых частей ограничений
Предположим, что предприятие хочет ежедневно увеличить приобретение первого сырья М1 до 28 тонн. Как это изменение повлияет на максимальный доход предприятия? По формуле ХВ=В-1 b и найдем новое решение задачи.
Таким образом, текущие базисные переменные с новыми значениями по-прежнему составляют допустимое решение. Соответствующее этому решению оптимальное значение целевой функции равно 24 тыс.руб.
Если увеличить ежесуточное приобретение второго сырья М2 до 8 тонн, оставляя сырье М1 на прежнем уровне 24 тонны, то получим совсем другую картину.
Полученное решение не является допустимым, поскольку s 4 =-1. Для возврата в область допустимых решений применим двойственный симплекс-метод для соответствующей симплекс-таблицы. Отметим, что она отличается от последней симплекс- таблицы примера 1.1 только столбцом «Решение».
| Базис | z | x1 | x2 | s1 | s2 | s3 | s4 | Решение | |
| z | 1 | 0 | 0 | 3/4 | 1/2 | 0 | 0 | 22 | |
| х 1 | 0 | 1 | 0 | 1/4 | -1/2 | 0 | 0 | 2 | |
| х 2 | 0 | 0 | 1 | -1/8 | 3/4 | 0 | 0 | 3 | |
| s3 | 0 | 0 | 0 | 3/8 | -5/4 | 1 | 0 | 0 | |
| s4 | 0 | 0 | 0 | 1/8 | -3/4 | 0 | 1 | -1 |
В соответствии с двойственным симплекс-методом исключаемой переменной будет s 4, а вводимой – s 2. В результате получим следующую симплекс-таблицу с оптимальным допустимым решением. (В общем случае для получения оптимального решения может потребоваться несколько итераций двойственного метода).
| Базис | z | x1 | x2 | s1 | s2 | s3 | s4 | Решение | |
| z | 1 | 0 | 0 | 5/6 | 0 | 0 | 2/3 | 64/3 | |
| х 1 | 0 | 1 | 0 | 1/6 | 0 | 0 | -2/3 | 8/3 | |
| х 2 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 2 | |
| s3 | 0 | 0 | 0 | 1/6 | 0 | 1 | -5/3 | 5/3 | |
| s 2 | 0 | 0 | 0 | -1/6 | 1 | 0 | -4/3 | 4/3 |
Интервалы допустимых изменений для элементов b
Другой способ исследования влияния изменения доступности ресурсов (т.е. элементов вектора b правых частей неравенств ограничений) заключается в определении интервалов допустимости для этих элементов, сохраняющих текущее решение допустимым.
Заменим вектор b вектором
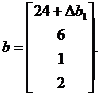
Для того чтобы текущее базисное решение осталось допустимым, необходимо выполнение неравенства ХВ=В-1 b 1 >=0. Отсюда получаем следующую систему неравенств:
Первое неравенство порождает 
второе 
третье 
и четвертое 
. Это эквивалентно следующему двойному неравенству для приращения 
Таким образом интервал допустимости для b 1 получается следующий: 
.
Аналогично получим интервал допустимости и для b 2
Тогда
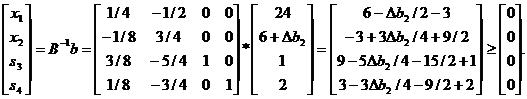
Первое неравенство порождает 
второе 
третье 
и четвертое 
. Это эквивалентно следующему двойному неравенству для приращения 
Таким образом интервал допустимости для b 2 получается следующий: 
.
Если сравнивать этот результат для интервалов допустимости для ресурсов с результатами элементарного графического исследования на чувствительность, проведенного в теме 1, то можно обнаружить точное совпадение.
Определение интервалов допустимости для ресурсов b i вышеприведенным способом корректно только когда изменения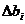 
рассматриваются независимо друг от друга, только тогда в пределах интервала допустимости ресурса bi итоговое приращение целевой функции 
(что следует из первой теоремы о двойственности) пропорционально приращению ресурса и двойственной цене ресурса.
Одновременное изменение ресурсов намного сложнее, ведь приходится решать линейную систему неравенств от многих переменных. Поэтому при изменении сразу нескольких ресурсов, ведущих к недопустимому решению, следует применить двойственный симплекс-метод и получить новое решение и значение целевой функции и сравнить с прежним решением.
Добавление новых ограничений
Добавление нового ограничения в существующую модель ЛП может привести либо к ситуации, когда ограничение избыточное, когда оно выполняется при текущем оптимальном решении, тогда ограничение просто отбрасывается, либо к ситуации, когда новое неравенство не выполняется при текущем оптимальном решении, тогда необходимо применить двойственный симплекс-метод, чтобы получить новое оптимальное решение.
