Задачей целочисленного линейного программирования (ЦЛП) называется отыскание минимума или максимума линейной целевой функции, где переменные удовлетворяют линейным ограничениям, целочисленные и неотрицательные.
 (5.1)
(5.1)
 (5.2)
(5.2)
Множество точек 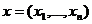 , удовлетворяющих ограничениям (5.2) в n -мерном евклидовом пространстве, представляют выпуклый многогранник, который называется областью допустимых решений (ОДР). По условию задачи необходимо найти вектор
, удовлетворяющих ограничениям (5.2) в n -мерном евклидовом пространстве, представляют выпуклый многогранник, который называется областью допустимых решений (ОДР). По условию задачи необходимо найти вектор  с целочисленными координатами, принадлежащий ОДР, в котором целевая функция (1) достигает своего глобального оптимума.
с целочисленными координатами, принадлежащий ОДР, в котором целевая функция (1) достигает своего глобального оптимума.
Методы решения задач ЦЛП основаны на использовании вычислительных возможностей методов ЛП. Обычно алгоритмы ЦЛП включают три шага:
Шаг 1 Ослабление пространства допустимых решений задачи ЦЛП путем замены любой двоичной переменной y непрерывным ограничением  и отбрасывания требования целочисленности для всех остальных переменных. В результате получается обычная задача ЛП.
и отбрасывания требования целочисленности для всех остальных переменных. В результате получается обычная задача ЛП.
Шаг 2 Решение задачи ЛП и определение его оптимального решения.
Шаг 3 Имея полученное (непрерывное) оптимальное решение, добавляем специальные ограничения, которые итерационным путем изменяют пространство допустимых решений задачи ЛП таким образом, чтобы, в конечном счете, получилось оптимальное решение, удовлетворяющее требованиям целочисленности.
Метод ветвей и границ
Рассмотрим следующую задачу ЦЛП
Пример 5.1
 (5.3)
(5.3)
На рисунке 5.1 пространство решений задачи ЦЛП представлено точками. Соответствующая начальная задача ЛП (обозначим ее ЛП0) получается путем отбрасывания целочисленности. Ее оптимальным решением будет х1=3,75, х2=1,25 и z =23,75.

Рисунок 5.1 - Пространство допустимых решений задачи ЦЛП
Оптимальное решение задачи ЛП0 не удовлетворяет условию целочисленности, метод ветвей и границ изменяет пространство решений задачи ЛП так, что в конечном счете получается оптимальное решение задачи ЦЛП. Для этого сначала выбирается одна из целочисленных переменных, значение которой в оптимальном решении не является целочисленным. Например, х1=3,75, замечаем, что область 3<х1<4 пространства допустимых решений задачи ЛП0 не содержит целочисленных значений переменной х1 и, следовательно, может быть исключена из рассмотрения, как бесперспективная. Это эквивалентно замене исходной задачи ЛП0 двумя новыми задачами линейного программирования ЛП1 и ЛП2, которые определяются следующим образом:
пространство допустимых решений ЛП1 = пространство допустимых решений ЛП0+ (х1≤3),
пространство допустимых решений ЛП2 = пространство допустимых решений ЛП0+(х1≥4).
На рисунке 5.2 изображены пространства допустимых решений задач ЛП1 и ЛП2. Оба пространства содержат все допустимые исходной ЦЛП, т.е. не потеряют ни одной целой точки начальной задачи ЦЛП.
Если мы продолжим разумно исключать из рассмотрения области, не содержащие целочисленных решений (такие, как 3<х1<4), путем введения надлежащих ограничений, то в конечном счете получим задачу ЛП, оптимальное решение которой удовлетворяет требованиям целочисленности. Другими словами будем решать задачу ЦЛП путем решения задач ЛП.
Новые ограничения взаимоисключаемы, так что задачи ЛП1 и ЛП2 необходимо рассматривать как независимые задачи ЛП, что показано на рисунке 5.3. Дихотомия задач ЛП – основа концепции ветвления в методе ветвей и границ. Переменная х1 называется переменной ветвления.

Рисунок 5.2 - Пространства допустимых решений задач ЛП1 и ЛП2
Оптимальным решением задачи ЛП1 (которое может быть получено, например, симплекс-методом) является х1=3, х2=2 и z=23.
Оптимальное решение задачи ЛП1 удовлетворяет требованию целочисленности. В этом случае говорят, что задача ЛП1 прозондирована.
Мы не можем в этой ситуации оценить качество целочисленного решения, полученного из рассмотрения задачи ЛП1, ибо решение задачи ЛП2 может привести к более лучшему целочисленному решению (с большим значением целевой функции z). Пока мы можем сказать, что значение z=23 является нижней границей оптимального (максимального) значения целевой функции исходной задачи ЛЦП. Это значит, что любая нерассмотренная подзадача, которая не может привести к целочисленному решению с большим значением целевой функции, должна быть исключена из рассмотрения, как бесперспективная. Если же не рассмотренная подзадача может привести к лучшему целочисленному решению, то нижняя граница должна быть надлежащим образом изменена.
При нижней границе z=23 исследуем задачу ЛП2 (единственную оставшуюся нерассмотренной подзадачу). Так как в задаче ЛП0 оптимальное решение равно 23,75 и все ее коэффициенты являются целыми числами, то невозможно получить целочисленное решение задачи ЛП2 (пространство которой более узко, чем ЛП0), которое будет лучше имеющегося. В результате мы отбрасываем задачу ЛП2 и считаем ее прозондированной.
Реализация метода ветвей и границ завершена, так как обе подзадачи ЛП1 и ЛП2 прозондированы (рассмотрение первой привело к нахождению целочисленного решения, а второй к заключению, что ее возможное целочисленное решение не может быть лучше имеющегося). Следовательно, мы заключаем, что оптимальным решением задачи ЦЛП является решение, соответствующее нижней границе, а именно х1=3, х2=2 и z=23.
Граф решения задачи методом ветвей и границ приведен на рисунке 5.3.

Рисунок 5.3 - Схема решения задачи при выборе подзадачи для зондирования ЛП1
Остались без ответа два вопроса, связанные с реализацией описанной вычислительной процедуры.
1 Можно ли было в задаче ЛП0 выбрать переменную х2 в качестве переменной ветвления вместо х1?
2 Можно ли было при выборе подзадачи для зондирования решить сначала задачу ЛП2 вместо ЛП1?
Ответы на оба вопроса положительные. Однако последующие вычисления могут значительно отличаться. Ситуация, когда первой решается задача ЛП2, иллюстрируется схемой вычислений (рисунок 5.4).

Рисунок 5.4 - Схема решения задачи при выборе подзадачи для зондирования ЛП2
Последовательность решения подзадач, показанная на рисунке 5.4 (ЛП0, ЛП2, ЛП4, ЛП3, ЛП6, ЛП5, ЛП1), является наихудшей; тем не менее она встречается на практике. Этот пример указывает на основную слабость метода ветвей и границ: как выбирать следующую подзадачу для исследования и как выбирать для нее переменную ветвления?
В процессе решения, представленного на рисунке 5.3, мы случайно наткнулись на хорошую нижнюю границу значений целевой функции на самой первой подзадаче ЛП1, что позволило прозондировать ЛП2 без детальных исследований и закончить вычисления. По существу, мы завершили вычисления, решив лишь одну подзадачу. В процессе решения, представленном на рисунке 5.4, мы вынуждены исследовать семь подзадач, и лишь тогда завершились вычисления метода ветвей и границ. Хотя имеются эвристические соображения, позволяющие угадывать, какая из ветвей может привести к улучшенному решению задачи ЦЛП, не существует строгой теории, которая всегда обеспечивала надежные результаты.
Теперь сформулируем алгоритм метода ветвей и границ в общем случае. Зададим нижнюю границу оптимального значения целевой функции z задачи ЦЛП равной - ∞. Положим i=1.
Шаг 1 (Зондирование и определение границы). Выбираем i -ю подзадачу линейного программирования ЛПi для исследования. Решаем ЛПi и зондируем ее, при этом возможна одна из трех ситуаций:
а) оптимальное значение целевой функции задачи ЛПi не может улучшить текущей нижней границы;
б) ЛПi приводит к лучшему допустимому целочисленному решению, чем текущая нижняя граница;
в) ЛПi не имеет допустимых решений.
Возможны два случая:
а) если задача ЛПi прозондирована, нижняя граница изменяется только при условии, что найдено лучшее решение задачи ЦЛП. Если все задачи прозондированы, необходимо закончить вычисления: оптимальным решением задачи ЦЛП является то, которое соответствует текущей нижней границе, если такая существует. Иначе положить i=i+1 и повторить Шаг1;
б) если задача не прозондирована, переходим к Шагу 2 для выполнения ветвления.
Шаг 2 (Ветвление) Выбираем одну из целочисленных переменных хj, оптимальное значение хj* которой в оптимальном решении задачи ЛПi не является целым. Исключаем из пространства допустимых решений область 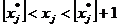 путем формирования двух подзадач ЛП, которые соответствуют ограничениям
путем формирования двух подзадач ЛП, которые соответствуют ограничениям  и
и  .
.
Положим i=i+1 и переходим к шагу 1.
Описанный алгоритм применим для решения задачи максимизации. Для решения задач минимизации в алгоритме необходимо заменить нижнюю границу верхней (начальное значение которой равно z=∞).






