Данный метод, как и метод ветвей и границ, начинает работу с оптимального решения «обычной» (непрерывной) задачи ЛП. Однако вместо ветвления и построения границ этот метод видоизменяет пространство допустимых решений, последовательно прибавляя специальным образом построенные ограничения (именуемые отсечениями). При этом само нецелочисленное оптимальное решение отсекается, а все целочисленные решения остаются в области допустимых решений. В результате конечного числа итераций получаем оптимальное целочисленное решение. Рассмотрим сначала идею этого метода на графическом примере, а затем покажем, как отсечения строятся алгебраически.
Продемонстрируем идею метода для решения следующей задачи ЛЦП.
Пример 5.2
(5.4)
Данный метод путем добавления (отсекающих плоскостей) преобразует пространство допустимых решений соответствующей задачи ЛП в выпуклый многогранник, вершина которого, соответствующая оптимуму, является целочисленной и представляет решение исходной задачи. На рисунке 5.5 показан пример двух таких отсечений. Мы начинаем с оптимального решения непрерывной задачи ЛП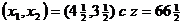 
. Затем прибавляем отсечение I, которое вместе с ограничениями исходной задачи ЛП приводит к оптимальному решению 
. После этого прибавляется отсечение II, которое вместе с отсечением I и исходными ограничениями приводит к оптимальному решению 
. Последнее решение является полностью целочисленным, как и требуется.
Рисунок 5.5 - Графическое представление метода отсечений
Прибавленные отсечения не отбрасывают ни одной исходной допустимой целочисленной точки, но должны проходить, по меньшей мере, через одну целочисленную точку (допустимую или недопустимую). Этим основным требованиям должно удовлетворять любое отсечение. В общем случае может потребоваться любое (но конечное) число отсечений для достижения полностью целочисленной экстремальной точки. В действительности количество отсечение не зависит от размерности задачи.
Алгебраический способ определения отсечений
Метод отсекающих плоскостей начинает работу с решения непрерывной задачи ЛП. В симплекс-таблице, соответствующей оптимальному решению задачи ЛП, следует выбрать одну из строк (чаще в качестве таковой ее берут строку с максимальной дробной частью свободного члена), для которой базисная переменная нецелочисленная. Искомое отсечение строится на основании дробных составляющих коэффициентов этой строки (называемой производящей). По этой причине его называют дробным отсечением.
Сейчас мы выведем уравнение дробного отсечения на примере решения системы (5.4).
Оптимальная (последняя) симплекс-таблица представлена в таблице 5.1
Таблица 5.1
| Базис | z | x1 | x2 | х3 | х4 | Решение |
| z | 1 | 0 | 0 | 63/22 | 31/22 | 133/2 |
| х2 | 0 | 0 | 1 | 7/22 | 1/22 | 7/2 |
| х1 | 0 | 1 | 0 | -1/22 | 3/22 | 9/2 |
Оптимальным непрерывным решением нашей задачи (5.4) является 
.
В качестве производящей выберем х2 -строку
.
Разложим каждый коэффициент производящей строки на целую и дробную части, при условии, что дробная часть всегда положительна и находится в пределах от 0 до 1
.
Перепишем равенство в следующем виде:
.
Поскольку 
, выражение в скобках является неотрицательным. Поэтому величина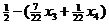 
, будучи целочисленной, не может превышать 1. Следовательно, необходимое условие целочисленности можно записать следующим образом:
.
Это и есть отсечение, порожденное х2 - строкой. Нетрудно убедиться, что ранее найденное оптимальное непрерывное решение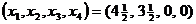 
не удовлетворяет отсечению (т.к. х3=0 и х4=0 и тогда получается, что 1/2≤0). Следовательно, если мы присоединим отсечение к последней симплекс-таблице, то оптимальное решение новой симплекс-таблицы будет двигаться в направлении выполнения ограничения целочисленности.
Превратим последнее неравенство путем добавления избыточной переменной х5 в равенство 
и добавим в последнюю симплекс-таблицу 5.1. Получается таблица 5.2.
Таблица 5.2
| Базис | z | x 1 | x 2 | х3 | х4 | х5 | Решение |
| z | 1 | 0 | 0 | 63/22 | 31/22 | 0 | 133/2 |
| х2 | 0 | 0 | 1 | 7/22 | 1/22 | 0 | 7/2 |
| х1 | 0 | 1 | 0 | -1/22 | 3/22 | 0 | 9/2 |
| х5 | 0 | 0 | 0 | -7/22 | -1/22 | 1 | -1/2 |
Таблица представляет оптимальное, но недопустимое решение. Для восстановления допустимости решения применим двойственный симплекс-метод, рассмотренный нами в теме 3. В результате получим следующую таблицу.
Таблица 5.3
| Базис | z | x1 | x2 | х3 | х4 | х5 | Решение |
| z | 1 | 0 | 0 | 0 | 1 | 9 | 62 |
| х2 | 0 | 0 | 1 | 0 | 0 | 1 | 3 |
| х1 | 0 | 1 | 0 | 0 | 1/7 | -1/7 | 32/7 |
| х3 | 0 | 0 | 0 | 1 | 1/7 | -22/7 | 11/7 |
Из-за дробных значений переменных х1 и х3 последнее решение все еще нецелочисленное. Выберем х1 -строку в качестве производящей, т.е.
.
Соответствующее отсечение имеет вид
.
Присоединяя последнее отсечение к симплекс-таблице 5.3, получаем:
Таблица 5.4
| Базис | z | x1 | x2 | х3 | х4 | х5 | х6 | Решение |
| z | 1 | 0 | 0 | 0 | 1 | 9 | 0 | 62 |
| х2 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 3 |
| х1 | 0 | 1 | 0 | 0 | 1/7 | -1/7 | 0 | 32/7 |
| х3 | 0 | 0 | 0 | 1 | 1/7 | -22/7 | 0 | 11/7 |
| х6 | 0 | 0 | 0 | 0 | -1/7 | -6/7 | 1 | -4/7 |
После применения двойственного симплекс-метода получим:
Таблица 5.5
| Базис | z | x1 | x2 | х3 | х4 | х5 | х6 | Решение |
| z | 1 | 0 | 0 | 0 | 0 | 3 | 7 | 58 |
| х2 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 3 |
| х1 | 0 | 1 | 0 | 0 | 0 | -1 | 1 | 4 |
| х3 | 0 | 0 | 0 | 1 | 0 | -4 | 1 | 1 |
| х4 | 0 | 0 | 0 | 0 | 1 | 6 | 7 | 4 |
Оптимальное решение, определяемое последней симплекс-таблицей, является целочисленным. Мы останавливаемся на этом.
Важно подчеркнуть, что применение дробного отсечения предполагает целочисленность всех переменных, включая дополнительные. Это значит, что данный метод применим только к решению полностью целочисленных задач.
Контрольные вопросы
1 В чем заключается идея метода ветвей и границ?
2 Назовите главные недостатки метода ветвей и границ.
3 Как связаны между собой двойственный симплекс-метод и метод отсекающих плоскостей?
4 Почему метод отсекающих плоскостей не применяется для решения частично целочисленных задач?
