В предыдущих разделах мы доказали, что конечное оптимальное решение задачи ЛП достигается в крайних точках пространства решений. А все крайние точки можно определить алгебраически как базисные решения системы линейных уравнений 
Таким образом, чтобы найти оптимальное решение ЛП, достаточно рассматривать только базисные решения указанной системы уравнений.
При выполнении симплекс-метода мы начинали с допустимого базисного решения В, затем переходили к следующему допустимому базисному решению, которое улучшает (по крайней мере не ухудшает) значение целевой функции, и так до тех пор, пока не будет достигнуто оптимальное решение. Таким образом, допустимое базисное решение В – это тот принципиальный элемент в симплекс-методе, вокруг которого выполняются все вычисления в симплекс-таблице. С этой точки зрения очевидна необходимость представления симплекс-таблицы в матричной форме.
В канонической форме задача ЛП
разобьем вектор Х на два – Х I и ХII, таких что вектор ХII соответствует начальному базису В, т.е. является начальным допустимым решением. Вектор С также разобьем на два вектора С I и СII в соответствии с векторами Х I и ХII. Тогда стандартную задачу ЛП можно записать следующим образом:
Для любой симплексной итерации будем обозначать через ХВ базисный вектор переменных, а через СВ – вектор коэффициентов целевой функции, соответствующих этому базису. Поскольку все небазисные переменные равны нулю, каноническая задача ЛП будет сведена к задаче с целевой функцией z=C BXB и ограничениями BXB =b, где текущее решение удовлетворяет следующему уравнению:
Симплекс таблица получается из исходной задачи ЛП путем вычислений по следующей формуле:
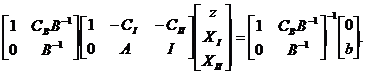
Выполнив вычисления по этой формуле, получаем симплекс-таблицу:
| Базис | ХI | XII | Решение |
| z | CBB-1A-CI | CBB-1-CII | CBB-1b |
| XB | B-1A | B-1 | B-1b |
В этой таблице предварительных вычислений требует только обратная матрица B -1, так как другие элементы таблицы CB, CI, CII, A и b получаются из исходных данных задачи.
Представленная симплекс-таблица имеет большое значение, так как является основой всех вычислительных алгоритмов линейного программирования.
В симплекс-методе решение переходит от одного базиса В к следующему Вслед путем замены в В базисного вектора (исключаемого) на небазисный (вводимый). Определение вводимых и исключаемых векторов основано на следующих условиях оптимальности и допустимости.
Условие оптимальности симплекс-метода
Из матричного представления симплекс-таблицы следует, что коэффициент при переменной x j в z -строке равен
где P j - j -й столбец матрицы (А,I), c j – j -й элемент вектора С. Отметим, что разность 
всегда равна нулю для базисных переменных x j. Если обозначить через NB множество индексов небазисных переменных, тогда можно записать следующее уравнение для целевой функции
Из этого уравнения следует, увеличение значения небазисной переменной хj приводит к возрастанию (убыванию) значения целевой функции z выше текущего значения C BB -1b только в том случае, если разность строго отрицательна (положительна). В противном случае переменная хj не может улучшить текущее решение и должна остаться небазисной с нулевым значением.
Условие допустимости симплекс-метода
Определение исключаемого из базиса вектора основано на проверке ограничения, представленного в виде равенства, соответствующего i -й базисной переменной. Это равенство имеет следующий вид:
Запись (V) i означает i -й элемент вектор-столбца V.
Обозначим через Pk вводимый вектор, определенный из условия оптимальности, а через х k – вводимую в базис переменную, принимающую положительное значение. Поскольку все остальные небазисные переменные сохраняют нулевые значения, равенство ограничения, соответствующего базисной переменной 
, можно записать следующим образом:
Это уравнение показывает, что при 
возрастание переменной х k не приведет к отрицательному значению базисной переменной только в том случае, если будет выполняться неравенство
Таким образом, максимальное значение вводимой переменной х k можно вычислить по следующей формуле:
Базисная переменная, на которой достигается этот минимум, становится исключаемой.
Пример 1.1 Проиллюстрируем матричное представление симплекс-метода.
Пусть B=(P1, P 4, P 5, P 6) является допустимым базисом.
a) Покажем, что решение B не является оптимальным.
b) Найдем вводимый в базис и исключаемый из него векторы и Bслед.
На основании B=(P1, P 4, P 5, P 6) имеем X B =(x 1, s 2, s 3, s 4) и С B =(5, 0, 0, 0). Вычисляем обратную матрицу B-1
Находим текущее базисное решение
откуда получаем z=CBXB =5*4+0*2+0*5+0*2=20.
Аналогично получим коэффициенты в ограничениях после первой итерации при х1 и х2
Для проверки оптимальности базиса B=(P1, P 4, P 5, P 6) вычислим разности для текущих небазисных переменных х2 и s1:
(z2-c2, z3-c3)=CBB-1[P2, P3]- (c2, c3)=
Легко видеть, что все коэффициенты совпадают с коэффициентами в задаче ЛП из примера 1.1 после первой итерации симплекс-метода.
| Базис | z | x1 | x2 | s1 | s2 | s3 | s4 | Решение | |
| z | 1 | 0 | -2/3 | 5/6 | 0 | 0 | 0 | 20 | |
| х 1 | 0 | 1 | 2/3 | 1/6 | 0 | 0 | 0 | 4 | |
| s2 | 0 | 0 | 4/3 | -1/6 | 1 | 0 | 0 | 2 | |
| s3 | 0 | 0 | 5/3 | 1/6 | 0 | 1 | 0 | 5 | |
| s4 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 2 |
Поскольку в данной задаче следует максимизировать целевую функцию, разность z2– c 2 =-2/3 показывает, что базис X B =(x 1, s 2, s 3, s 4) неоптимален и значение целевой функции можно увеличить, если ввести переменную x 2.
Для того чтобы ввести в базис переменную х2, из него нужно исключить одну из четырех базисных переменных. Для определения исключаемой переменной вычисляем X B и B-1P2.
Значение вводимой переменной х2 равно
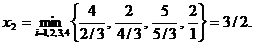
Таким образом, в базисе X B =(x 1, s 2, s 3, s 4) вектор P4 будет заменен на P 2, что приводит к новому базису
.
Соответствующее новое значение целевой функции равно z =20-(-2/3)*3/2=21.
Можно пересчитать и вторую итерацию симплекс-метода с помощью матриц и убедиться, что все совпадет со второй итерацией симплекс-метода этого примера.
Анализ чувствительности
Анализ чувствительности выполняется уже после получения оптимального решения задачи ЛП. Его цель – определить, приведет ли изменение коэффициентов исходной задачи к изменению текущего оптимального решения, и если да, то как эффективно найти новое оптимальное решение (если оно существует).
В общем случае изменение коэффициентов исходной задачи может привести к одной из следующих ситуаций:
1 Текущее базисное решение остается неизменным.
2 Текущее решение становится недопустимым.
3 Текущее решение становится неоптимальным.
4 Текущее решение становится неоптимальным и недопустимым.
Во второй ситуации можно использовать двойственный симплекс-метод для восстановления допустимости решения. В третьей ситуации мы используем прямой симплекс-метод для получения нового оптимального решения. В четвертой ситуации для получения нового оптимального и допустимого решения следует воспользоваться как прямым, так и двойственным симплекс-методом. Четвертая ситуация, как комбинация второй и третьей, будет рассмотрена позже.
Для объяснения различных процедур анализа чувствительности используем пример 1.1 производства краски.
| Исходная задача | Двойственная задача |
| 
|
| 
|
| 
|
Приведем также последнюю симплекс-таблицу этого примера.
| Базис | z | x1 | x2 | s1 | s2 | s3 | s4 | Решение | |
| z | 1 | 0 | 0 | 3/4 | 1/2 | 0 | 0 | 21 | |
| х 1 | 0 | 1 | 0 | 1/4 | -1/2 | 0 | 0 | 3 | |
| х 2 | 0 | 0 | 1 | -1/8 | 3/4 | 0 | 0 | 3/2 | |
| s3 | 0 | 0 | 0 | 3/8 | -5/4 | 1 | 0 | 5/2 | |
| s4 | 0 | 0 | 0 | 1/8 | -3/4 | 0 | 1 | 1/2 |
