Текущее оптимальное решение перестает быть оптимальным, если разности 
не удовлетворяют условию оптимальности. Используя вектор двойственных цен 
, запишем 
.
Отсюда следует, что на оптимальность решения влияют только коэффициенты сj целевой функции (и, следовательно, вектор СВ) и/или нормы потребления ресурсов, представленные векторами P j. Рассмотрим последовательно каждый фактор, влияющий на оптимальность решения.
Изменение коэффициентов целевой функции
Для определения влияния изменений коэффициентов целевой функции следует пересчитать разности только для небазисных переменных, поскольку при любых изменениях коэффициентов сj, соответствующих базисным переменным, разности всегда остаются равными нулю.
Вычислительная процедура заключается в следующем.
1 Вычисляется вектор двойственных цен для нового вектора коэффициентов СВ.
2 Вычисляются разности 
для текущей небазисной переменной х j. При этом возможны два варианта:
а) если условие оптимальности выполняется, текущее решение остается оптимальным, но значение целевой функции может измениться;
б) если условие оптимальности не выполняется, следует применить (прямой) симплекс-метод для получения нового оптимального решения.
Рассмотрим сквозной пример 1.1. Предположим, что изменились цены на производимую продукцию фирмы. Стоимость тонны краски для наружных работ стала равна 6 тыс.руб. и для краски для внутренних работ 5 тыс.руб. за тонну. Как будет соотноситься новое базисное решение со старым?
Получаем новую целевую функцию для этой модели:
максимизировать z =6x 1 +5x 2.
Поскольку текущее базисное решение состоит из переменных 
имеем СВ=(6, 5, 0, 0). Вычислим вектор двойственных цен.
.
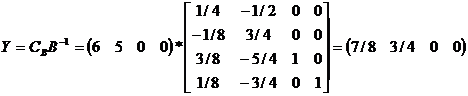Разности для небазисных переменных s1, s 2 равны
Новое значение целевой функции равно 25,5.
Кроме того, для исследования влияния коэффициентов целевой функции на оптимальность решения можно также вычислить (по отдельности) интервалы изменения каждого коэффициента, сохраняющие оптимальность текущего решения. Для этого следует заменить коэффициент с j выражением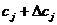 
.
Ограничения на величины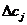 
можно определить путем вычисления новых разностей и наложения на них соответствующего условия оптимальности.
Пусть 
. Найдем 
из условия
или
Откуда получаем систему неравенств
которая эквивалентна следующему двойному неравенству 
. То есть интервал изменения коэффициента с1, сохраняющий оптимальность текущего решения, равен 
.
Пусть 
. Найдем 
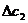из условия
или
Имеет смысл рассматривать только первые две координаты вектора Y, что приводит нас к системе неравенств
которая эквивалентна двойному неравенству 
. То есть интервал изменения коэффициента с2, сохраняющий оптимальность текущего решения, равен 
.
Точно такие же интервалы изменения коэффициентов целевой функции, сохраняющие оптимальное текущее решение, были получены в результате элементарного графического исследования на чувствительность, проведенного в теме 1 для этого же примера.
Добавление в модель ЛП нового вида производственной деятельности
Введение в модель линейного программирования нового вида производственной деятельности эквивалентно добавлению новой переменной в задачу ЛП. Добавление нового вида производственной деятельности интуитивно обосновано только в том случае, если деятельность экономически рентабельна, то есть улучшает оптимальное значение целевой функции. Это условие можно проверить путем вычисления для новой переменной разности 
, где Y –вектор оптимальных значений двойственной задачи; P j, с j – соответствующие нормы потребления для этого нового вида производственной деятельности и стоимость единицы продукции. Если вычисленное значение разности удовлетворяют условию оптимальности, то новый вид деятельности нежелателен, поскольку не улучшает оптимального решения. И наоборот.
Контрольные вопросы
1 Назовите последовательность действий в двойственном симплекс-методе.
2 Как найти интервалы допустимых изменений для ресурсов?
3 Как определить интервалы изменения коэффициентов целевой функции, сохраняющие оптимальность текущего решения задачи ЛП?
4 Что подразумевают под анализом на чувствительность оптимального решения задачи ЛП?
