Связь между оптимальными решениями двойственных задач устанавливается с помощью теорем о двойственности.
Теорема 1 Если одна из двойственных задач имеет оптимальное решение, то другая также имеет оптимальное решение, причем для любых оптимальных решений 
и 
выполняется равенство
(3.5)
Если одна из двойственных задач неразрешима ввиду того, что 
то другая задача не имеет допустимых решений (ограничения противоречивы).
Экономический смысл первой теоремы о двойственности. План производства х=(х1, x2, …, xn) и набор цен на ресурсы y=(y 1, y 2, …, ym) оказывается оптимальным тогда и только тогда, когда прибыль от реализации продукции, полученная при «внешних» (известных заранее) ценах c1, c 2, …, cn, равна затратам на ресурсы по «внутренним» (определяемым только из решения задачи) ценам y1, y 2, …., ym. Для всех остальных планов x и y обеих задач прибыль от продажи продукции всегда будет меньше (или равна) затратам на ресурсы.
Другими словами, предприятию безразлично, производить ли продукцию по оптимальному плану и получить максимальную прибыль 
либо продавать ресурсы по оптимальным ценам и возместить от продажи равные ей минимальные затраты на ресурсы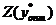 
.
Теорема 2 (о дополнительной нежесткости) Для оптимальности решений и пары двойственных задач необходимо и достаточно, чтобы они удовлетворяли системе уравнений
(3.6)
Теоремы 1,2 позволяют определить оптимальное решение одной из пары двойственных задач по решению другой.
Двойственные оценки являются:
· показателем дефицитности ресурсов и продукции. Это свойство следует из теоремы 1: величина 
является оценкой i -го ресурса; чем больше значение оценки , тем выше дефицитность ресурса; для недефицитного ресурса 
;
· показателем влияния ограничений на значение целевой функции. Из теоремы 1 следует, что при незначительном приращении D bi является точной мерой влияния ограничений на целевую функцию. Поэтому практический интерес представляет определение предельных значений ограничений (нижней и верхних) границ, в которых величины оценок остаются неизменными;
· показателем эффективности производства отдельных видов продукции с позиций критерия оптимальности. Это свойство следует из теоремы 2; его суть заключатся в том, что в оптимальный план может быть включена лишь та продукция j-го вида, для которой выполняется условие
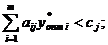
· инструментом сопоставления суммарных условных затрат и результатов. Это свойство следует из теоремы 1, в которой устанавливается связь между значениями целевой функции прямой и двойственной задач.
