Последовательность шагов алгоритма решения транспортной задачи в точности повторяет аналогичную последовательность этапов симплексного алгоритма.
Шаг 1 Определяем начальное базисное решение, затем переходим к выполнению второго шага.
Шаг 2 На основании условия оптимальности симплекс-метода среди всех небазисных переменных определяем вводимую в базис. Если все небазисные переменные удовлетворяют условию оптимальности, вычисления заканчиваются; в противном случае переходим к третьему шагу.
Шаг 3 С помощью условия допустимости симплекс-метода среди текущих базисных переменных определяем исключаемую. Затем находим новое базисное решение. Возвращаемся ко второму шагу.
Связь метода потенциалов с симплекс-методом основывается на соотношениях двойственности задач ЛП. Исходя из специальной структуры транспортной задачи (6.1), двойственная ей задача будет записана в следующем виде.
 (6.2)
(6.2)
Из соотношений двойственности следует, что коэффициент при переменной хij в выражении целевой функции должен быть равен разности между левой и правой частями соответствующего ограничения двойственной задачи, т.е величине ui +vj -cij. Но мы знаем, эта величина по второй теореме о двойственности для каждой базисной переменной равна нулю. Другими словами, для этих переменных должно выполняться равенство ui +vj =cij. Имея m+n-1 таких равенств и решая их как систему линейных уравнений (после присвоения какой-либо переменной произвольного значения, например u1 =0), находим значения потенциалов ui и v j. Вычислив значения потенциалов, далее определяем вводимую в базис переменную среди всех небазисных как переменную, имеющую наибольшее положительное значение величины ui +vj -cij.
Присвоение одной из двойственных переменных произвольного значения (например u1=0) противоречит представлениям о том, что двойственное решение единственно, ведь оно находится как произведение вектора коэффициентов целевой функции при базисных переменных на обратную матрицу коэффициентов при базисных переменных ограничений (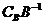 ). Но это не так, и можно показать, что значение целевой функции не меняется при замене C B на СB+k, что присвоение одной двойственной переменной произвольного значение равносильно прибавлению к коэффициентам целевой функции произвольной константы k ко всем коэффициентам с ij.
). Но это не так, и можно показать, что значение целевой функции не меняется при замене C B на СB+k, что присвоение одной двойственной переменной произвольного значение равносильно прибавлению к коэффициентам целевой функции произвольной константы k ко всем коэффициентам с ij.
Алгоритм решения транспортной задачи будет проиллюстрирован на следующем примере 6.1
Пример 6.1
Транспортная компания занимается перевозкой зерна специальными зерновозами от трех элеваторов к четырем мельницам. В таблице 6.1 показаны возможности отгрузки зерна (предложения) элеваторами (в зерновозах) и потребности (спрос) мельниц (также в зерновозах), а также стоимости перевозки зерна одним зерновозом от соответствующего элеватора к соответствующей мельнице. Стоимость перевозок с ij приведена в сотнях тысяч рублей.
Таблица 6.1
| мельницы | 1 | 2 | 3 | 4 | предло- | ||||||
| элеваторы | жение | ||||||||||
| 1 | 10 | 2 | 20 | 11 | |||||||
| x 11 | x 1 2 | x 1 3 | x 1 4 | 15 | |||||||
| 2 | 12 | 7 | 9 | 10 | |||||||
| x2 1 | x22 | x23 | x24 | 25 | |||||||
| 3 | 4 | 14 | 16 | 18 | |||||||
| x31 | x32 | x33 | x34 | 10 | |||||||
| Спрос | 5 | 15 | 15 | 15 | 50 | ||||||
|
| |||||||||||
В данной задаче требуется определить структуру перевозок между элеваторами и мельницами с минимальной стоимостью. Для этого необходимо найти объемы перевозок xij между i -м элеватором и j -й мельницей.




