Общая форма задачи линейного программирования (ЛП) обычно записывается следующим образом:
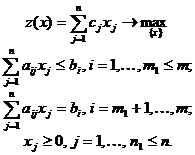
(2.1)
Условия задачи (2.1) называются смешанными, ибо в них присутствуют ограничения типа равенств и типа неравенств.
В матричной форме задача ЛП (2.1) приобретает вид
(2.2)
Набор чисел x1, x 2, …, xn, или вектор x, удовлетворяющий системе ограничений, называется планом рассматриваемой задачи ЛП. Компоненты вектора х называются составляющими плана.
Каждому плану х соответствует определенное значение функции z(x). Чем больше z(x), тем лучше план. План, для которого z(x) достигает максимума, называется оптимальным планом х0, т.е. z (x 0) ≥ z (x), где х - любой план задачи (2.1).
В дальнейшем будем предполагать, что область допустимых планов – ограничена и непуста.
В теории ЛП рассматривают три формы задачи ЛП:
a) каноническую 
(2.3)
b) сопряженную каноническую 
c) форму с однотипными ограничениями 
Покажем теперь, что любую линейную задачу можно привести к канонической форме. Для этого необходимо научиться переходить от ограничений типа неравенств к ограничениям типа равенств и от переменных х j, на которые не наложено условие неотрицательности, к неотрицательным переменным.
1 Каждое неравенство 
переходит в равенство при сложении левой части неравенства с новой неотрицательной переменной 
2 Если n 1 <n, то каждая переменная 
на которую не наложено условие неотрицательности, заменяется разностью новых неотрицательных переменных
Приме р 2.1 Привести к канонической форме записи задачу ЛП
x 1 +x 2 =max, -x 1 +x 2 ≤ -1, 2x 1 +x 2 =2, x 1 ≥ 0, x 2 -свободная переменная.
Первое ограничение запишем в форме равенства введением новой переменной х3≥0: - x 1 +x 2 +х3=-1. Так как на x 2 не наложено условие неотрицательности, то заменяем х2 разностью двух новых неотрицательных переменных 
После этих преобразований исходная задача ЛП запишется в канонической форме:
Некоторые свойства планов
Во всех аналитических методах решение задачи ЛП ищется последовательными приближениями. Вначале задается допустимое решение, которое затем улучшается в направлении движения к экстремуму целевой функции.
Мы в этом разделе рассмотрим несколько теорем, позволяющих провести анализ решения задачи ЛП. Предполагаем, что наша задача приведена к каноническому виду на максимум.
Теорема 1 Множество всех планов задачи ЛП выпукло.
Доказательство: Возьмем два плана задачи ЛП, заданной в канонической форме:
Необходимо показать, что выпуклая комбинация из точек 
и 
, является планом.
.
То есть х является планом.
Аналогично можно показать по индукции, что выпуклая комбинация любых планов задачи ЛП также является планом.
Линейная форма ограничений задачи (2.3) приводит к тому, что граница G (если оно непустое) состоит из кусков ряда гиперплоскостей. G может либо пустым множеством, либо выпуклым многогранником, либо выпуклой многогранной областью, уходящей в бесконечность. Для облегчения изложения дальнейшего материала будем предполагать, что область G ограничена, т.е. представляет собой выпуклый многогранник.
Мы должны найти из бесконечного множества точек множества G найти точку, в которой достигается максимум целевой функции z (x). Решение этой проблемы облегчается тем фактом, что замкнутую многогранную область G порождает конечное число особых точек (крайних точек), являющихся вершинами многогранника. Крайней точкой называют точку множества G, которая не может быть представлена как линейная комбинация двух других точек из множества G. Остальные точки G являются выпуклыми комбинациями крайних точек, т.е. как говорят в теории множеств, G является выпуклой оболочкой своих крайних точек.
Теорема 2 Линейная форма z(x)=c Tx задачи ЛП достигает своего максимума в крайней точке выпуклой области планов G. Если z(x) достигает максимума более чем в одной крайней точке, то она достигает того же значения в любой другой точке, являющейся выпуклой комбинацией этих точек.
Доказательство: Обозначим крайние точки области G (вершины выпуклой многогранной области) через х(1), …, х(k), оптимальный план – через 
. Считаем, что максимум достигается только в одной точке х0, т.е. z(x 0)>z (x), х Î G.
Покажем, что х0 может быть только крайней точкой области G. Если она не крайняя, то она может быть представлена выпуклой комбинацией крайних точек:
Рассчитаем z(x0), учитывая линейность функции z:
Пришли к противоречию. Следовательно, x0 может быть только крайней точкой области G.
Предположим далее, что существует несколько крайних точек х(1), …, х(m), в которых целевая функция z(x) достигает своего максимального значения:
z (x (1))=…=z (x (m))=z 0 º z (x 0). Тогда в точках 
величина z (x) также достигает максимального значения 
Теорема доказана.
Определение. План x задачи ЛП, заданной в канонической форме (2.3), называется невырожденным опорным планом, если число ненулевых компонент плана х равно рангу матрицы А, и векторы столбцы матрицы А, соответствующие ненулевым компонентам х, линейно независимы.
В (2.3) матрица А имеет размер (m× n). Будем считать для простоты, что ранг r=m, т.е. матрица А имеет m линейно независимых столбцов.
Определение. Система m линейно независимых столбцов 
матрицы A называется базисом опорного плана х (в векторе х компоненты 
положительны, а остальные нулевые) и обозначается B x.
Примем без доказательства следующую теорему.
Теорема 3 План хT=(х1, х2, …,х n) является крайней точкой G в том и только в том случае, если он опорный.
Сформулируем основные результаты раздела.
1 Множество планов задачи ЛП соответствует множеству точек выпуклого многогранника G.
2 Множество опорных планов соответствует множеству крайних точек многогранника G.
3 Каждой крайней точке соответствует базис из m векторов из данной системы n векторов-столбцов матрицы А.
4 Оптимальный план находится среди опорных (базисных).
Все конечные методы решения ЛП основываются на переборе тем или иным способом опорных планов и выборе из них оптимального.
Алгоритм симплекс-метода
Алгоритм симплекс-метода находит оптимальное решение, рассматривая ограниченное число допустимых базисных решений (опорных планов).
Алгоритм начинается всегда с некоторого допустимого опорного плана и затем пытается найти другой опорный базисный план, «улучшающий» значение целевой функции. Это возможно только в том случае, если возрастание какой-либо нулевой (небазисной) переменной ведет к улучшению значения целевой функции. Но для того, чтобы небазисная переменная стала положительной, надо одну из текущих базисных сделать нулевой (небазисной). Это необходимо, чтобы новое допустимое решение содержало в точности m базисных переменных. В соответствии с терминологией симплекс-метода выбранная нулевая переменная называется вводимой (в базис), а удаляемая базисная переменная – исключаемой (из базиса).
Алгоритм рассмотрим для наглядности на примере 1.1.
Приведем систему (1.1), (1.2) к каноническому виду:
Здесь 
- дополнительные переменные (остаточные), добавленные в неравенства для преобразования их в равенства.
Задачу ЛП в канонической форме для удобства будем представлять в виде таблицы 2.1.
Таблица 2.1
| Базис | z | x1 | x2 | s1 | s2 | s3 | s4 | Решение | |
| z | 1 | -5 | -4 | 0 | 0 | 0 | 0 | 0 | z-строка |
| s1 | 0 | 6 | 4 | 1 | 0 | 0 | 0 | 24 | s1-строка |
| s2 | 0 | 1 | 2 | 0 | 1 | 0 | 0 | 6 | s 2 -строка |
| s3 | 0 | -1 | 1 | 0 | 0 | 1 | 0 | 1 | s3 -строка |
| s4 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 2 | s4 -строка |
Нижние четыре строки представляют равенства ограничений; значения правых частей этих равенств даны в столбце «Решение». Строка z получена из равенства z-5x1-4 x 2 =0.
Дополнительные переменные составляют очевидное начальное допустимое базисное решение, которое отображается в столбце «Решение»: 
При этом 
они не базисные. Значение целевой функции при этом базисном решении равно нулю.
Будет ли начальное решение оптимальным? Конечно, нет, поскольку переменные х1 и х2 здесь равны нулю, а возрастание этих переменных даже на единицу приводит к увеличению значения целевой функции z=5x1+4 x 2 на 5 единиц или 4. Поскольку коэффициент при х1 больше, чем при х2, переменную х1 следует ввести в базис (в этом случае она станет вводимой). Если обратиться к таблице 2.1, то вводимая переменная определяется среди небазисных как переменная, имеющая наибольший отрицательный коэффициент в z-строке.
Включаемая переменная х1 должна принимать положительное значение. На рисунке 1.1 видно, что, исходя из начальной точки А (х1=0, х2=0), наибольшее значение, которое можно присвоить переменной х1 (не выходя из множества допустимых решений), равно 4, что соответствует точке В (х1=4, х2=0). Это означает, что решение переместилось от крайней точки А в крайнюю точку В.
Алгебраически точку пересечения можно найти как отношение правой части равенства (значение в столбце «Решение») к коэффициенту при переменной х1 в этом равенстве, как показано в таблице 2.2.
Таблица 2.2
| Базис | х1 | Решение | Отношение |
| s1 | 6 | 24 | 24/6=4 (минимум) |
| s2 | 1 | 6 | 6/1=6 |
| s3 | -1 | 1 | 1/(-1) = -1 (не подходит) |
| s4 | 0 | 2 | 2/0 = ∞ (не подходит) |
При этом нас интересуют только неотрицательные отношения (или точка пересечения на положительной полуоси х1), так как они соответствуют направлению возрастания переменной х1. Отметим, что все значения в столбце «Решение» неотрицательны, поэтому вычисляемое отношение будет неотрицательным и конечным только в том случае, если знаменатель отношения строго положителен. Именно поэтому мы не рассматриваем отношения, соответствующие третьему и четвертому равенствам, так как там знаменатели или отрицательны, или равны нулю.
Минимальное неотрицательное отношение равно значению вводимой переменной х1 в новом решении, а именно х1 = 4. Значение целевой функции возрастает при х1 = 4 до 20 (=5 × 4).
Теперь среди текущих базисных переменных следует определить исключаемую переменную, которая примет значение ноль после выведения ее из базиса и введения в базис переменной х1. (В нашем примере количество базисных переменных должно быть равно ровно 4). Поскольку наименьшее (неотрицательное) отношение соответствует переменной s1, то в точке В, именно эта переменная обращается в нуль. Таким образом, переменная s1 будет исключаемой, в этом случае переменная х1 автоматически получает значение, равное 4. Замена исключаемой переменной s1 на вводимую х1 приводит к новому базисному решению 
Вычисление нового базисного решения основывается на методе исключения переменных (методе Гаусса-Жордана). Для этого определим ведущий столбец, ассоциируемый с вводимой переменной, и ведущую строку, ассоциируемую с исключаемой переменной. Элемент, находящийся на пересечении ведущего столбца и ведущей строки называется ведущим элементом.
Для нашего примера ведущий столбец переменной х1 и ведущая строка s1 в таблице 2.1 выделены серой заливкой. Ведущим элементом будет число 6.
Процесс вычисления нового базисного решения состоит из двух этапов.
1 Вычисление элементов новой ведущей строки.
Новая ведущая строка = Текущая ведущая строка / Ведущий элемент.
2 Вычисление элементов остальных строк, включая z-строку.
Новая строка = Текущая строка - ее коэффициент в ведущем столбце* новая ведущая строка.
В нашем примере ведущая строка (s1 - строка) делится на ведущий элемент (=6). Вычисляем элементы остальных строк таблицы.
a) z - строка.
| т екущая z-строка: | (1 | -5 | -4 | 0 | 0 | 0 | 0│ | 0) |
| -(-5)*Новая ведущая строка: | (0 | 5 | 10/3 | 5/6 | 0 | 0 | 0│ | 20) |
| = Новая z- строка: | (1 | 0 | -2/3 | 5/6 | 0 | 0 | 0│ | 20) |
b) s2 - строка.
| т екущая s2 -строка: | (0 | 1 | 2 | 0 | 1 | 0 | 0│ | 6) |
| - (1)*Новая ведущая строка: | (0 | -1 | -2/3 | -1/6 | 0 | 0 | 0│ | -4) |
| = Новая s2 - строка: | (0 | 0 | 4/3 | -1/6 | 1 | 0 | 0│ | 2) |
c) s3 - строка.
| т екущая s3 -строка: | (0 | -1 | 1 | 0 | 0 | 1 | 0│ | 1) |
| + (1)*Новая ведущая строка: | (0 | 1 | 2/3 | 1/6 | 0 | 0 | 0│ | 4) |
| = Новая s3 - строка: | (0 | 0 | 5/3 | 1/6 | 0 | 1 | 0│ | 5) |
d) s4 - строка. Новая s4 - строка повторяет текущую s4 - строку, поскольку ее коэффициент в ведущем столбце равен нулю.
Новая симплекс таблица, соответствующая новому базисному решению, имеет вид.
Таблица 2.3
| Базис | z | x1 | x2 | s1 | s2 | s3 | s4 | Решение | |
| z | 1 | 0 | -2/3 | 5/6 | 0 | 0 | 0 | 20 | |
| х 1 | 0 | 1 | 2/3 | 1/6 | 0 | 0 | 0 | 4 | |
| s2 | 0 | 0 | 4/3 | -1/6 | 1 | 0 | 0 | 2 | |
| s3 | 0 | 0 | 5/3 | 1/6 | 0 | 1 | 0 | 5 | |
| s4 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 2 |
Отметим, что новая таблица 2.3 обладает теми же свойствами, что и начальная таблица 2.1: только небазисные переменные х2 и s1 равны нулю, в столбце «Решение» представлено новое базисное решение (
) вместе с новым значением целевой функции z (=20). Это результат применения метода Гаусса-Жордана.
Из последней таблицы видно, что полученное базисное решение не является оптимальным, поскольку в z -строке переменная х2 имеет отрицательный коэффициент. Увеличение значения х2 (ее текущее значение равно нулю) приведет к увеличению значения целевой функции. Таким образом, х2 должна быть введена в базис.
Далее определим исключаемую переменную. Для этого вычислим отношения правых частей равенств, соответствующих ограничениям, к коэффициентам, стоящим при х2 в этих равенствах.
Таблица 2.4
| Базис | x2 | Решение | Отношение |
| x1 | 2/3 | 4 | 4/(2/3)=6 |
| s2 | 4/3 | 2 | 2/(4/3)=3/2 минимум |
| s3 | 5/3 | 5 | 5/(5/3) = 3 |
| s4 | 1 | 2 | 2/1 = 2 |
В этой ситуации ведущей строкой будет s2 -строка, а ведущим столбцом- столбец, соответствующий переменной х2. Ведущий элемент равен 4/3. В таблице 2.3 они отмечены заливкой.
Далее опять ведущую строку (s2 - строка) делим на ведущий элемент (4/3) и с помощью этой новой строки избавляемся от х2 во всех остальных строках, включая z - строку. В результате получится таблица 2.5.
Таблица 2.5
| Базис | z | x1 | x2 | s1 | s2 | s3 | s4 | Решение | |
| z | 1 | 0 | 0 | 3/4 | 1/2 | 0 | 0 | 21 | |
| х 1 | 0 | 1 | 0 | 1/4 | -1/2 | 0 | 0 | 3 | |
| х 2 | 0 | 0 | 1 | -1/8 | 3/4 | 0 | 0 | 3/2 | |
| s3 | 0 | 0 | 0 | 3/8 | -5/4 | 1 | 0 | 5/2 | |
| s4 | 0 | 0 | 0 | 1/8 | -3/4 | 0 | 1 | 1/2 |
Поскольку z -строка не имеет отрицательных коэффициентов, соответствующих небазисным переменным s1 и s 2, полученное решение оптимально.
Найденное оптимальное решение вместе с дополнительными переменными будет 
Значение целевой функции z =21.
C помощью последней симплекс-таблицы 2.5 можно получить много дополнительной информации, кроме решения:
1 Состояние ресурсов.
2 Цена единицы ресурсов.
3 Все данные, необходимые для проведения анализа на чувствительность.
Это подробно будет описано в следующих темах.
Сформулируем два правила, а также рассмотрим последовательность действий, выполняемых при реализации симплекс-метода.
Условие оптимальности
Вводимой переменной в задаче максимизации (минимизации) являетсянебазисная переменная, имеющая наибольший отрицательный (положительный) коэффициент в z -строке. Если в z -строке есть несколько таких коэффициентов, то выбор вводимой переменной берется произвольно. Оптимальное решение достигнуто тогда, когда в z -строке все коэффициенты при небазисных переменных будут неотрицательными (неположительными).
Условие допустимости
Как в задаче минимизации, так и в задаче максимизации в качестве исключаемой выбирается базисная переменная, для которой отношение правой части ограничения к положительному коэффициенту ведущего столбца минимально. Если базисных переменных с таким свойством несколько, то выбор исключаемой переменной выполняется произвольно.
Последовательность действий, выполняемых в симплекс-методе
Шаг 0 Находится начальное допустимое решение.
Шаг 1 На основе условия оптимальности определяется вводимая переменная. Если вводимых переменных нет, вычисления заканчиваются.
Шаг 2 На основе условия допустимости выбирается исключаемая переменная.
Шаг 3 Методом Гаусса-Жордана вычисляется новое базисное решение. Переход к шагу 1.
Контрольные вопросы
1 Как формулируется задача ЛП в общем виде?
2 Как привести задачу ЛП к канонической форме?
3 Назовите последовательность действий, выполняемых в симплекс-методе.
4 Какие свойства допустимых решений вы знаете?
5 Как будет себя вести симплекс-метод при неединственном решении задачи ЛП?
