Пусть дана общая задача линейного программирования (ЛП):
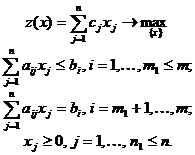(3.1)
Двойственной к ней задачей называется задача следующего вида:
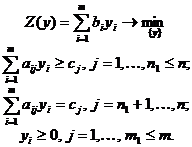(3.2)
Задачи (3.1) и (3.2) образуют пару взаимно-двойственных задач. Задача (3.2), двойственная к задаче (3.1), строится по правилам:
1 Упорядочивается запись исходной задачи, т.е. если целевая функция задачи максимизируется, то ограничения-неравенства должны иметь знак ≤, если минимизируется, то знак ≥. Выполнение этих условий можно достичь умножением соответствующего ограничения на (-1) в случае необходимости.
2 Каждой переменной y i двойственной задачи соответствует i -е ограничение исходной задачи, и наоборот, каждой переменной х j исходной задачи соответствует j -е ограничение двойственной задачи.
3 Если исходная задача является задачей максимизации, то двойственная задача будет задачей минимизации и наоборот. При этом вектор, образованный из коэффициентов при неизвестных целевой функции исходной задачи, совпадает с вектором констант в правых частях ограничений двойственной задачи. Аналогично связаны между собой векторы, образованные из коэффициентов при неизвестных целевой функции двойственной задачи, и константы в правых частях ограничений исходной задачи.
4 Матрица из коэффициентов при неизвестных в ограничениях двойственной задачи AT образуется транспонированием матрицы A=(aij)m ×n, составленной из коэффициентов при неизвестных в ограничениях исходной задачи.
5 Если на j -ю переменную исходной задачи наложено условие неотрицательности, то j -е ограничение двойственной задачи будет являться неравенством, а в противном случае это ограничение будет равенством. Аналогично связаны между собой ограничения исходной задачи и переменной двойственной задачи.
Можно дать экономическую интерпретацию пары двойственных задач. Рассмотрим задачу рационального использования ресурсов (исходную задачу). Пусть предприятие располагает запасами ресурсов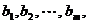 
которые могут использоваться для выпуска n видов продукции. Известна стоимость единицы j-го вида продукции c j (j =1,2,…,n) и нормы потребления i-го ресурса a ij (i=1,…, m) на производство j -го вида продукции. Требуется определить объем производства продукции каждого вида хj (j =1,…,n), при котором суммарная стоимость выпуска продукции будет максимальной:
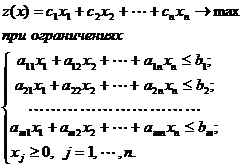(3.3)
По задаче ЛП (3.2) сформулируем другую экономическую задачу (двойственную).
Предположим, что некоторая фирма может закупить все ресурсы, которыми располагает предприятие. Необходимо определить оптимальные цены y i (i=1,…,m) на эти ресурсы, исходя из условия, что покупающая фирма стремится минимизировать общую стоимость ресурсов. Следует также учитывать и то, что фирма должна уплатить сумму, не меньшую, которую может выручить предприятие при организации собственного производства продукции.
Математическая модель имеет следующий вид:
(3.4)
Здесь Z(y) – общая оценка ресурсов. Каждое j -е ограничение из задачи (3.4) представляет собой неравенство, левая часть которого равна оценке всех ресурсов, расходуемых на производство единицы j -го вида продукции, а правая – стоимости единицы продукции.
Задачи (3.3) и (3.4) образуют симметричную пару взаимно двойственных задач.
Цены ресурсов y1, y 2, …., ym получили различные названия: учетные, неявные, теневые. Смысл в том, что это условные ненастоящие цены. В отличие от «внешних» цен c1, c 2, …, cn на продукцию, известных до начала производства, цены ресурсов y1, y 2, …., ym являются внутренними, поскольку они не задаются извне, а определяются в результате решения задачи, поэтому их называют оценками ресурсов.
