Статическая неопределимость.
Основная система – ОС, эквивалентная система- ЭС.
Если систему нельзя рассчитать с помощью только уравнения статики, то такая система является статически неопределимой.
Например: имеем четыре реакции опоры, а уравнений статики три.
Расчет начинают с установления числа лишних с точки зрения неизвестных или что тоже самое степени статической неопределенности по формуле
Л = 2Ш + Со –3Д (1)
Ш – число простых шарниров, равно числу сходящихся шарниров – 1
Со – число опорных связей
Д –число дисков
Л = 2 · 1 + 6 – 3 · 2 = 2
Удаление всех линейных связей превращает заданную систему в статически определенную простую систему.
При удалении связей нужно помнить что ОС должна являться неизменной и неподвижной.
При удалении нужного числа линий связи можно пользоваться таблицей.
| № | Способ освобождения связей | ЗС | ОС | ЭС | Число ос-ых связ. |
| 1 | Удаление опорного стержня | 
| 
| 
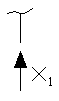
| 1 |
| 2 | Удаление Шарнирного Незагруженного Стержня | 
|
| 
| 1 |
| 3 | Введение Шарнира | 
| 
| 
| 1 |
| 4 | Удаление Шарнира | 
|
| 
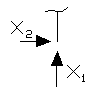
| 2 |
| 5 | Рассечение Стержня | 
|
| 
| 3 |
Эквивалентная система образуется путем загружения основной системы заданными нагрузками, а так же неизвестными реакциями удаленных связей. Эквивалентность означает что перемещения по направлениям отброшенных связей от всех нагрузок, включая и неизвестные реакции, должны отсутствовать.
Аналогическим выражением условий эквивалентности являются канонические методом сил.
Канонические уравнения.
Введем обозначения: Di – перемещение по направлению отброшенной связи i от всех нагрузок и воздействий; Dik - перемещение по направлению отброшенной связи i от действия реакции катой связи Хк; D if - перемещение по направлению отброшенной связи i от действия всех заданных нагрузок; d ik - перемещение по направлению отброшенной связи i от действия реакции Хк = 1.
Определим Di используя принцип независимости действия сил
Di = Di1 + Di2 + Di3 +… + Dik + … + Din + Dif = 0 (1)
Выразим перемещение Dik через перемещения от единичных воздействий Dik = dik · Хк
Тогда уравнение (1) примет следующий вид
di1 · x1 + di2 · x2 + di3 · x3 + … + Din · xn + Dif (2)
Если имеем n лишних связей, то нужно составить n подобных уравнений
d11 · x1 + d12 · x2 + d13 · x3 + … + D1n · xn + D1f
d21 · x1 + d22 · x2 + d23· x3 + … +D2n · xn + D2f
………………………………………………… (3)
dn1 · x1 + dn2 · x2 + dn3 · x3 + … + Dnn · xn + Dnf
Уравнения системы (3) называются каноническими уравнениями метода сил.
Физический смысл первого уравнения – перемещение точки приложения реакции первой отброшенной связи по направлению этой реакции от всех нагрузок и воздействий равно 0. Другие уравнения аналогично.
Решают систему (3) относительно Xi, вычислив предварительно коэффициент dik и свободные члены Dif. Для этого нужно построить в основной системе N + 1 эпюру изгибающих моментов:
Эпюра М1 только от х1 = 1
Эпюра М2 только от х2 = 1
…………………………….
Эпюра Mn только от хn = 1
Эпюра МF только от заданных нагрузок
эпюры с черточками М1 – Mn называются единичными, а эпюра МF – грузовой.
Полученные эпюры перемножают между собой в определенной последовательности. Например, чтобы определить dik, нужно перемножить эпюры dik = эп. М1 · эп. МК с учетом жесткостей определенных участков.
Коэффициенты с одинаковыми индексами называются главными и они всегда положительные. Остальные коэффициенты называются побочными, причем dik = dki.
Системой линейных алгебраических уравнений, а значит может быть решена любым известным из математическим способом.
Построить эпюру изгибающих моментов для заданной системы.
Эпюру М будем строить используя принцип независимости действия нагрузок. Предварительно строят исправленные эпюры, которые получают путем умножения единичных эпюр на соответствующие неизвестные
эп. М1 = х1 · эп. М1
эп. М1 = х1 · эп. М1
Далле строят эпюру моментов заданной системы путем суммирования всех исправленных и грузовой эпюр. Эп. М = эп. М1 + эп. М2 + … + эп. Mn + эп. МF
Процесс исправления эпюры состоит в умножении ординат в характерных точках одной эпюры на составляющее неизвестное. Если x < 0, то исправленная эпюра переворачивается по отношению к единичной.
Процесс сложения эпюр состоит в сложении ординат в характерных точках исправленных и грузовой эпюр.
Построенная эпюра подлежит проверкам: статистической и деформационной.
Статистическая – проверка равновесия жесткости узлов.
Деформационная – проверка, состоящая в перемещении эпюры М и любой единичной эпюры.
Результат перемножения должен примерно равняться 0. Допустима погрешность 1 –3 %. Статическая проверка носит формальный характер и свидетельствует лишь о правильности сложения эпюр.
Физический смысл деформационной проверки состоит в отрицании перемещения в направлении отброшенной связи.
Построение эпюр поперечных и продольных сил для заданной системы.
Если результат деформационной проверки положителен, то переходят к построению эпюры поперечных сил Q, используя зависимость Q = dM / dx
На прямолинейных участках эпюры М величина Q определяется как тангенс угла наклона эпюры М к оси. При этом tg a > 0 если ось до совершения с эпюрой М нужно повернуть по ходу часовой стрелки на острый угол.
tg a > 0
tg a = (a - b) / l
tg a = (a + b) / l
Если эпюра М прямолинейна, то рассмотрим равновесие данного участка под действием:
а) заданной распределенной нагрузки q
б) известность сосредоточенного момента на границах участка
в) неизвестность поперечных сил Q
Примечание: Q направляют так, чтоб она стремилась вращать рассматриваемый участок по часовой стрелки.
Под действием нагрузок участок должен быть в равновесии. Используя, условия равенства о сумме моментов относительно концов участка составляют и решают уравнения равновесия.
Например:
Q1 -?
å m2 = 0
Q1 · l – M1 – q · l · l/2 + M2 = 0
Q1 =
Q2 · l + M2 + q · l · l/2 - M1 = 0
Q2 =
Полученные положительные ординаты откладывают вверх от горизонтальных участков и влево от вертикальных. Ординаты в соседних характерных точках соединяются прямыми.
Эпюру продольных сил М строят по эпюрам поперечных сил Q. Для этого рассматривают равновесие узлов рамы. Под действием известных поперечных сил (см. эпюру Q).
Положительные поперечные силы прикладывают к узлу так, чтобы они вращали узел по ходу часовой стрелки. Неизвестные продольные силы направляют от узла. Если величина продольной силы известна, то её направление зависит от знака: если N > 0,то её направление от узла и наоборот. Затем используя условие равновесия в виде сумм проекций сил на рационально ориентированные оси составляют и решают уравнения равновесия. Вычисляют ординаты по обе стороны от оси и указывают знаки.
Окончательная статическая проверка.
Изображают заданную систему загруженными заданными нагрузками и реакциями опор. Составляют три уравнения равновесия, используя три уравнения равновесия
å х = 0 
å у = 0
å m = 0 (моментной точкой может быть любая).
Реактивную силу совпадающую с осью рамы на опоре определяют
по эпюре N > 0, то реакцию направляют от рамы и наоборот.
Реактивную силу перпендикулярную оси рамы на опоре определяют по эпюре Q: если Q на опоре больше 0, то реакцию направляют так, что она вращала раму по часовой стрелки. Если есть защемляющая опора, то реактивный момент направлен в сторону противоположной ординате эпюры М на опоре.
Лекция 13.
Расчет статически неопределимых систем методом перемещений.
Постановка задачи. Неизвестные методы перемещения.
Под действием заданной нагрузки все точки упругой системы получают перемещения. Перемещения бывают двух видов: 1) линейные (измеряются в метрах); 2) угловые (измеряются в радианах). Рассмотрим пример деформирования П - образной рамы
D1 - линейное, горизонтальное
перемещение группы узлов 1 и 2
j1 - угол поворота узла 1
j2 - угол поворота узла 2
D1 · j1 - суть перемещения
характерных точек.
С помощью метода сил для заданной рамы можно построить эпюру изгибающих моментов, а потом определить перемещения, но возможен и другой путь расчета: сначала определить характерные точки, а потом по ним строят эпюры Q, M, N. Такая постановка задачи приводит к методу перемещений. Неизвестными метода перемещений являются угловые перемещения жестких узлов.
Степень кинематической неопределимости.
Общее число неизвестных метода перемещений (степень кинематической неопределимости) устанавливается по формуле n = n у+ n л (1), где л и у число независимых угловых коэффициентов рамы не считая защемляющей опоры.
n у = 2 n л - число независимых двух узлов.
Рассмотрим использование формулы (1) на примере расчетных схем двух рам.
а) б)
Схема а) имеет один жесткий узел 2, значит n у = 1.
Схема б) имеет два жестких узла 1 и 4, значит n у = 2.
Чтобы определить n л образуют условную шарнирную систему.
Условную шарнирную систему строят путем введения шарниров в все жесткие узлы включая и опорные защемления. При этом защемляющие опоры преобразуются в шарнирно-неподвижные, а консольные участки отбрасывают. Заданные шарнирные опоры остаются при этом неизменными.
Условная шарнирная система.
а) б)
W = 3 · 3 – 2 · 2 – 4 = 1 W = 3 · 4 – 2 · 3 – 6 = 0
n w = 1 n w = W = 0
n мис = 0 n мис = 1
n л – 1 + 0 = 1 n л = 0 + 1 = 1
Произведем кинематический анализ данных условной шарнирной системы.
Схема а) может в результате перемещения узлов 1 и 2 по дуге окружности перемещаться.
Схема б) является мгновенно изменяемой системой (мис).
Узел 1 может перемещаться по вертикали только на небольшую величину. При этом в стержнях 01 и 12 возникнут очень большие усилия, которые могут привести к разрушению этих стержней. Траектория их движения окружности. Признак (мис) – три шарнира, расположенных на одной прямой или средний шарнир не подкреплен.
n л можно определить как минимально необходимое число опорных связей, которые нужно присоединить к подвижным узлам так чтобы условная шарнирная система была статически неизменяемой.
а) б)
Можно определить n л аналитически по формуле
n л = n w + n мис (2)
n w = число жестких узлов
n мис = число линейных смещений жестких узлов (3)
W = 3Д – 2Ш – Со
n мис – степень мгновенной изменяемости системы равная числу троек шарниров лежащих на одной прямой.
Основная система.
Если в методе сил основной системы получают путем удаления лишних связей, то в методе перемещений основной системы образуют путем введения дополнительных связей.
В каждый жесткий узел вводится плавающая заделка. Она должна удерживать узел от поворота, но не препятствовать его линейному смещению. Число вводимых плавающих заделок должно быть = n у.
Кроме плавающих заделок вводятся дополнительные опорные стержни. Они исключают линейную подвижность групп узлов.
Правила установки дополнительных опорных стержней:
1) число дополнительных опорных стержней должно быть = n у
2) дополнительные опорные стержни присоединяют только к подвижным узлам условной шарнирной системы
3) дополнительные опорные стержни должны совпадать с направлением касательной с возможной траекторией движения подвижного узла условной шарнирной системы в начале движения
Например:
а)
б)
n у = 1
В а) дополнительные опорные стержни можно присоединить к 1 или 2, но лучше к 1 (нагляднее). Дополнительные опорные стержни расположены горизонтально.
В б) дополнительные опорные стержни можно присоединить к 1 или 4, не нарушая их жесткости.
Полученная основная система имеет статическую неопределенность выше чем заданная система, однако теперь имеем совокупность однопролетных статически неопределенных стержней для которых изгибающие моменты строятся сравнительно просто.
Эквивалентная система.
Сопоставим заданную и основную систему. Заданная система – жесткие узлы под действием нагрузок имеют возможность поворачиваться, а в основной системе – нет, значит, для того чтоб основная система стала эквивалентна заданной системе основной нужно плавающая заделка, а с ними и жесткие узлы повернуть на те же углы, на которые они повернуты в заданной системе.
При повороте плавающей заделки возникнут реактивные моменты, как результат сопротивления рамы к повороту. А так как в заданной системе в жестких узлах связей нет, то нужно потребовать равенство реактивных моментов плавающих заделок. Это и будет условием эквивалентности для плавающей заделки.
Заданный системы группы узлов могут иметь линейные перемещения, но в основной системе им препятствуют дополнительные опорные стержни, значит для получения эквивалентности дополнительных опорных стержней нужно линейно переместить на ту же величину, что и заданная система, но тогда в дополнительных опорных стержнях возникнут реактивные силы, которые должны быть равны нулю из-за отсутствия дополнительных опорных стержней в заданной системе. Это условие эквивалентности для дополнительных опорных стержней, таким образом условие эквивалентности является равенство Ri = 0, где Ri – реактивное усилие, сила или момент в i -той введенной связи.
Примечание: нумерация произвольна, но будучи принята должна быть обязательной для дальнейшей манипуляции движения.
i = 1; 2 … n – общее число неизвестных.
Вывод: эквивалентная система образована путем загружения основной системы заданными нагрузками и неизвестными перемещениями Zi. Индекс i соответствует N связи.
Примечание:
1) угловое перемещение обозначают как сосредоточенный момент и направляют всегда по часовой стрелке.
2) 
Линейные перемещения показывают как сосредоточенную силу, которую направляют вдоль оси дополнительных осевых стержней.
Канонические уравнения.
Они вытекают из условия эквивалентности. Проанализируем напряжения условий эквивалентности R 1=0 – которое означает равенство нулю реактивного усилия первой связи от всех кинематических воздействий. Если обозначенное R 1К – реактивное усилие одной связи от кинематического воздействия Zк, а R 1F – то же от всех силовых нагрузок, то
R 1= R 11 + R 12+ R 13+ R 1N+ R 1F = 0
Обозначим riК – это реактивное усилие, возникающее в той связи от кинематического воздействия Zк = 1, тогда реактивное усилие возникающее в одной связи от Zк = 1 будет riК . Если вместо Zк = 1 приложить Zк ¹ 1, то возникающая реакция будет пропорциональна Zк.
R 1К = riК · Zк
Отсюда вытекает первое каноническое уравнение
ri11· Z1 + ri12· Z2 + ri1N· ZN + R 1F = 0
ri21· Z1 + ri22· Z2 + ri2N· ZN + R 2F = 0
Физический смысл i – го канонического уравнения состоит в отрицании реактивного усилия возникающего в i –той дополнительной связи.
