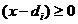От действия внешних сил, расположенных в одной из главных плоскостей инерции прямой балки, ось балки изгибается в той же плоскости. При этом точки оси балки получают вертикальные перемещения, а поперечные сечения балки получают некоторые повороты относительно их начального состояния.
Изогнутая ось балки называется упругой линией, а перемещения точек оси балки в направлении нормали к недеформированной оси, называются прогибами балки.
Прогиб оси балки в произвольной точке, расположенной на расстоянии x от начала координат, будем обозначать через v(x).
Угол поворота поперечного сечения балки, который находится на расстоянии x от начала координат, будем обозначать через φ(x).
Прогибы балки принимаются с положительным знаком, если они направлены вверх, а углы поворота имеют положительный знак, если поперечные сечения балки получают повороты, направленные против движения часовой стрелки. Прогибы балки измеряются в единицах длины (м, см), а углы поворота в радианах.
При изгибе балки длина ее оси не изменяется, потому что она расположена в нейтральном слое, где нормальные напряжения равняются нулю. Прогибы и углы поворота являются очень малыми величинами в сравнении с размерами балки.
Рис.1
На рис. начерчена прямолинейная ось балки до её нагружения, и криволинейная упругая линия, после нагружения балки. Произвольная точка оси балки, взятая на расстоянии x от начала координат, получает прогиб v(x). Поперечное сечение балки в этой точке получает поворот на угол φ(x). Этот угол равняется углу между касательной к упругой линии в данной точке и осью балки до деформации, или между нормалью к упругой линии в данной точке и поперечным сечением недеформированной балки.
Для определения прогибов и углов поворота необходимо составить дифференциальное уравнение изогнутой оси балки. Для этого используем известную зависимость между радиусом кривизны изогнутой оси балки r и изгибающим моментом M y , полученной при выводе формулы нормальных напряжений:
,
а также известную из курса высшей математики зависимость между радиусом кривизны и производными от уравнения изогнутой оси:
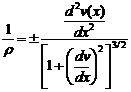
Приравняем правые части двух приведенных зависимостей и учтем, что при действии положительного изгибающего момента вторая производная от уравнения изогнутой оси балки также имеет положительный знак. Тогда будем иметь:
(15)
Первая производная от уравнения изогнутой оси балки по абсциссе x, которая содержится в знаменателе левой части зависимости (15), есть тангенс угла между осью x и касательной к упругой линии в произвольной точке. Учитывая, что углы поворота очень малые по сравнению с размерами балки (тангенсы этих углов практически не превышают 0,01 радиана), можем пренебречь квадратом первой производной в сравнении с единицей. Тогда дифференциальное уравнение изогнутой оси балки (или упругой линии) будет иметь вид:
(16)
или 
(17)
.
Определение перемещений в балках постоянной
жесткости методом начальных параметров
Рассмотрим часть балки длиной 
, нагруженную сосредоточенной силой F i, сосредоточенным моментом M i, равномерно распределенной нагрузкой q i, а также внутренними усилиями M y(0), Q z(0), которые действуют в начальном сечении балки, то есть в сечении, расположенном в начале координат (рис.2).
Рис. 2
Это сечение балки может иметь перемещения v(0) и φ(0), которые не показаны на рис.. Внутренние усилия M y(0), Q z(0) и перемещения v(0), φ(0), имеют название начальных параметров деформации балки при изгибе. Их значения зависят от условий закрепления балки на левом торце, то есть в начале системы координат.
Начало системы координат О всегда принимается на левом торце балки а ось x направляется вправо. Если, например, левый торец балки жестко закреплен, то начальный угол поворота и начальный прогиб балки равняются нулю, а начальные внутренние усилия равняются соответствующим реакциям жесткого закрепления со знаками изгибающего момента.
Более обстоятельно этот вопрос рассмотрим позже, когда будут получены уравнения углов поворота и прогибов упругой линии.
Направления действия всех внешних нагрузок и внутренних усилий, которые приведены на рис. 2 отвечают положительным знакам этих нагрузок и усилий.
Перемещения v(0) и φ(0) будем также считать положительными, то есть направленными вверх и против часовой стрелки.
Часть балки, которую мы рассматриваем, содержит 5 участков обозначенных римскими цифрами. Составим дифференциальное уравнение упругой линии (то есть изогнутой оси балки) для последнего правого участка балки, используя зависимость (17). Правая часть этой зависимости есть изгибающий момент в произвольном сечении последнего правого участка балки. Продолжим распределенную нагрузку q i до конца части балки, которую рассматриваем (то есть в пределах пятого участка), и чтобы не нарушить равновесие балки, приложим в пределах пятого участка такую же нагрузку - q i противоположного направления (рис.2).
Составим уравнение изгибающего момента в поперечном сечении последнего правого участка, который находится на переменном расстоянии x от начала координат. Чтобы это уравнение было структурированным относительно расстояния каждого вида нагрузки от рассматриваемого сечения, используем определение и правило знаков изгибающего момента, а также сосредоточенные моменты M y(0),и M i умножим на их расстояния от сечения, возведенные в нулевую степень. Тогда получим следующее уравнение изгибающих моментов на пятом участке:
(18)
Из уравнения (18) легко получить уравнение изгибающих моментов на любом участке, если сохранить в нем сумму моментов всех сил, которые действуют слева от конца этого участка.
Подставим в уравнение (18) вместо M y(x) его значение согласно зависимости (17) получим дифференциальное уравнение балки при изгибе:
(19)
Это уравнение всегда составляется для последнего правого участка балки, но оно используется для любого предыдущего участка. Для этого в правой части уравнения сохраняются моменты сил, которые действуют слева от рассматриваемого участка.
Интегрируем уравнение () дважды по независимой переменной x, используя прием Клебша (интегрируем без раскрытия скобок), получим соответственно уравнение углов поворота и прогибов поперечных сечений балки на пятом участке:
(20)
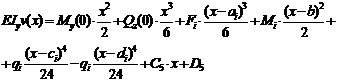(21)
Нетрудно доказать, что постоянные интеграции C5 и D5 для пятого участка равняются соответствующим постоянным интегрирования для любого участка и равняются начальным значением угла поворота и прогиба, умноженным на жесткость балки при изгибе (равенства C2= C1 и D2= D1=0 были получены в предыдущем параграфе).
В результате имеем:
C5 =C4= C3= C2= C1=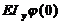 
(22)
D5= D4= D3= D2= D1= 
(23)
Заменим постоянные интегрирования в зависимостях (20) и (21) их значениями согласно (22) и (23), получим:
(24)
(25)
Зависимости (24) и (25) являются уравнениями углов поворота и прогибов балки на её произвольном участке. При составлении этих уравнений нужно учесть все нагрузки, которые действуют слева от рассматриваемого сечения балки. При этом нагрузки, которые действуют по часовой стрелке относительно сечения, учитываются с положительным знаком, а нагрузки, которые действуют против часовой стрелки относительно сечения, учитываются с отрицательным знаком.
Перед использованием составленных уравнений нужно определить начальные параметры из условий закрепления балки.
Если, например, балка шарнирно закреплена на двух концах и на левом торце не нагружена сосредоточенным моментом, то начальный изгибающий момент и начальное прогиб равняются нулю, то есть: M y(0)=0 и φ (0)=0. Начальная поперечная сила равняется вертикальной реакции левой опоры, а начальный угол поворота определяется из условия равенства нулю прогиба балки на правой опоре, то есть из условия: 
.
Если левый торец балки закреплен с помощью жесткой опоры, то начальный угол поворота и начальное прогиб балки равняются нулю, а начальный изгибающий момент и начальная поперечная сила равняются соответствующим реакциям жесткого закрепления. Знаки этих параметров принимаются в соответствии с направлениями действия реакций опоры по правилу знаков изгибающего момента и поперечной силы.
Если левый торец балки свободен от всякого закрепления, а правый торец имеет жесткую опору, то начальный изгибающий момент и начальная поперечная силы равняются нулю, или сосредоточенным нагрузкам того же характера на этом торце балки. Начальный прогиб и угол поворота неизвестны и их значения определяются из условий равенства нулю прогиба и угла поворота правого торца балки.
Если, наконец, левый торец балки свободен от всякого закрепления, а балка имеет две шарнирные опоры, то начальный прогиб и угол поворота неизвестны и их значения определяются из условий равенства нулю прогиба оси балки в точках закрепления шарнирными опорами.
Используя указанные условия и уравнения, составленные по типу уравнений (24) и (25) находим неизвестные начальные параметры, потом подставляем значение всех начальных параметров в те же зависимости (24) и (25), которые составлены для конкретной балки, и находим окончательные уравнения углов поворота и прогибов для произвольного участка балки.
Для определения величин угла поворота и прогиба в каком-либо сечении, нужно подставить в соответствующие уравнения значение абсциссы этого сечения и учесть только те нагрузки, которые действуют слева от этого сечения. Сосредоточенные силы Fi учитываем при условии, что 
, сосредоточенные моменты Mi учитываем при условии, что 
и распределенные нагрузки qi учитываем при условии, что 
, или 
