Выделим из тела в окрестности точки бесконечно малую треугольную призму, по основанию которой нормальные и касательные напряжения равны нулю.

Правило знаков любого σ > 0, если нормальные напряжения направлены от площадки; t > 0, если стремится вращать плоскость чертежа по ходу часовой стрелки; a > 0, если грань bc для совмещения с гранью ас нужно повернуть на острый угол против часовой стрелки.
Найдем равнодействующую силы приложенной к каждой грани призмы. Для этого нужно соответствующие напряжения умножить на площадь грани.
| Fx = σ x · dy · dz Fy = σ y · dx · dz Fa = σ a · ds · dz Tx = tx · dx · dz Ty = ty · dy · dz Ta = ta · ds · dz | 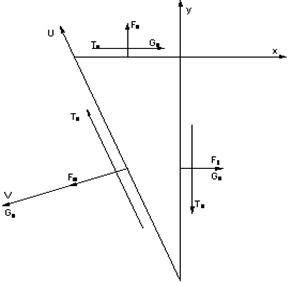
|
Эти равнодействующие силы должны удовлетворять всем условиям равнодействия. Проведём оси U и V, и реализуем шесть условий равновесия.
åU =0 Ta + Fy ·cos a - Tx · sin a - Fx · sin a - Ty ·cos a
Ta + cos a (Fy - Ty) – sin a (Tx + Fx) (1)
åV = 0 Fa - Fx · cos a+ Ty · sin a - Fx ·cos a - Fy ·sin a
Fa -Fx + Tx ·cos a + (Ty – Fy ·sin a) = 0 (2)
Сумма моментов относительно точки на оси å m0 = 0
å m0 = 0 Tx · dy/2 + Ty · dx/2 = 0 (3)
Подставим значения Tx и Ty и разделим обе части на dx/2 · dy dz
tx · dx/2 · dy dz + ty · dx/2 · dy dz = 0
tx + ty = 0
tx = - ty (4)
Касательные напряжения по двум взаимно-перпендикулярным площадям равны по модулю обратны по знаку. Зависимость (4) называется законом парности касательных напряжений. Из (4) следует что касательные напряжения направлены или к вершине прямого угла или от него.
Если подставить в зависимость (1) и (2) и заменить ty на - tч, а также учесть, что dx/ds = sin a, а dy/ds =cos a, то после преобразований получим значения нормальных и касательных напряжений по площадке повернутой относительно площадки с σх и σy на угол a.
σ a = σ x · cos2a + σ y · sin2a + tx · sin2a (5)
ty = ((σ x · σ y)/2) sin2a - tx · cos2a (6)
Если формулу (5) подставить в значение a и a ¹ 90°, то получим
σ a + σ (a+90°) = σ x + σ y = const. (7)
Вывод: сумму нормальных напряжений по двум взаимно- перпендикулярным площадкам является величиной постоянной, значит если на первой площадке имеем max нормальных напряжений, то по перпендикулярной ей площадке будут σ min.
Главные напряжения. Главные площади.
При инженерных расчетах нет необходимости в определении напряжений по всем площадкам проходящим через данную точку. Достаточно знать их экстремальные значения σmax и σmin, которые называются главными напряжениями, а площадки по которым они действуют называются главными площадками.
Чтобы получить экстремальное значение σ нужно первую производную от выражения (5) по углу a приравнять нулю.







Вывод: по главным площадкам касательные напряжения равны нулю.
tg2a0 =  (8)
(8)
tg2a0 =  (9)
(9)
Для определения положения главных площадок площадки по которым действуют σx и σy нужно повернуть на угол a0 против хода часовой стрелки, если a0 > 0.
Из формулы (8) 2a0 изменяется от –90° до 90°, а значит - 45°£a0 £45°, это значит, что поворот может быть на угол не более 45 °.
При определении главных напряжений значение a0 из (8) можно подставить в (5) или пользоватся формулой полученной из зависимости (6) и (9).
 (10)
(10)
Экстремальные касательные напряжения.
Площадки по которым действуют экстремальные касательные напряжения называют площадками сдвига.
Чтобы определить экстремальные касательные напряжения нужно, взяв первую производную от (6) по углу a приравнивая её к нулю.
 ;
;  ;
; 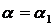
Разделим обе части уравнения на cos2a1 получим:
(σx - σy) + 2 tx tg2a1 = 0
tg2a1 =  (11)
(11)
Угол наклона плоскости с экстремальным касательным напряжением к площадке с dх нужно повернуть против хода часовой стрелки на угол a1.
Из формулы (11) можно получить a1 и a1+90, которые определяются двумя взаимно-перпендикулярными площадками. На одной из них будет действовать t max, а по другой tmin. Но в соответствии с законами парности касательных напряжений tmax = - tmin. Из сравнения (8) и (11) получим a1 ¹ a0+45°
Вывод: между главными площадками и площадками сдвига угол 45°
Подставив в формулу (6) σх = σmax; σy = σmin; tx = 0; a1 = + 45° получим
 = +
= +  (12)
(12)
подставим в (12) значение из (10) и после преобразований получим зависимость экстремальных касательных напряжений от напряжений по случайным площадям
 = + 1/2
= + 1/2  (13)
(13)
Круги Мора.
Пусть дано некоторое плоское напряженное состояние.

Построим для этого напряженного состояния круг Мора в системе прямоугольных координат.

Порядок действий:
1. по оси d отложим в максимальную величину dх
2. по оси t отложим значение ty
3. на пересечении получим точку А
4. аналогично отложим) dу и tх; точка А характеризует направление по вертикальным граням, точка В – по горизонтальным.
5. Соединим точки А и В и на пересечении с осью d получим точку О
6. Из точки О, как из центра круга проведем окружность
7. Определим радиус окружности из прямоугольного треугольника ОКВ
R = 
На пересечении горизонтальных и вертикальных площадок с окружностью получим точку С, которую назовём полюсом.
Теперь можно определить направление на любой площадке, для этого нужно параллельно заданной площадке провести через полюс прямую до пересечения с окружностью.
Точка М будет иметь координаты da и ta. Можно решить и обратную задачу, т. е. по значениям da и ta определить угол a.
Лекция 5.






