
Работа внешних сил.
Приложим, например, к торцу
консоли сосредоточенную силу,
которую будем медленно увели-
чивать от нуля до конечной вели-
чины F.
Медленное приложение нагрузки называется статическим. В процессе загружения консоли точка приложения силы переместится вниз на величину D - дельта.
Из курса физики известно, что величина дельта прямо пропорциональна силе F
D = a · F (1), где
a - коэффициент пропорциональности, зависящий от размеров, материала, расчетной схемы сооружения.
Увеличим F на бесконечно малую величину dF. Это увеличение силы вызовет приращение вертикального перемещения dD. Определим величину элементарной работы dW, внешние силы (F+dF) на перемещение dD.
dW = (F+ dF) · dD
dW = F· dD + dF · dD
где dF · dD - величина второго порядка малости, поэтому произведением dF · dD можно пренебречь. Тогда dW = F· dD.
Заменим D его значением из формулы (1)
dD = d (a · F) = a · dF
dW = F · a · dF
Чтобы величину всей работы совершённой сосредоточенной силой при её увеличении от нуля до конечного значения F нужно проинтегрировать это выражение
W = ò dW =ò F · a · dF = a ò FdF = a · F/2 ½F = a · F2/2 = F · aF/2
Учитывая (1) получим окончательное значение работы силы F при её статическом приложении
W = F ·D /2 (2)
Теорема Клайперона
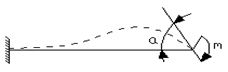
Работа внешней силы на упругом перемещении по направлению этой силы равно половине произведения конечной величины силы и перемещения. Если к системе статически приложен сосредоточенный момент, то величина работы
W = m · j / 2, гдеj- угол между касательной и осью в радианах.
Если на сооружение действует группа нагрузок, то полная работа
W = å (F1 · D1) /2 + å (mi · ji) /2, где D i j i - конечные перемещения силы Fi и mi соответственно. Эти перемещения вызваны действием всей группы сил.
Работа внутренних усилий.
Через стержень загруженный произвольными нагрузками проведем два поперечных сечения на расстоянии dx друг от друга.

M, Q, N – внутренние усилия, но по отношению участка они могут быть рассмотрены как внешние нагрузки. Если внешние нагрузки увеличивать статически, то внутренние усилия M, Q, N также возрастают статически. При этом они совершают работу на соответствующих им перемещениях. Воспользуемся принципом суперпозиций (независимого действия сил) и рассмотрим влияние на величину работы каждого усилия отдельно. Защемим например левое сечение элемента dx, а к правому сечению только силу N.

Под действием силы N правое сечение переместилось вправо на Ddx
В соответствии с законом Гука Ddx = Ndx / EA , EA – жесткость.
Определим элементарную работу совершенную силой N на перемещении Ddx
dWn = N · Ddx /2 = (N · N · dx) / 2EA
dWn = (N2 · dx) / 2EA
Аналогично загрузив правое сечение последовательно изгибающим моментом М и поперечной силой Q получим величины элементарных работ
dWm = (M2 · dx) / 2E · I
dWQ = m (Q2 · dx) / 2G · A
m - поправочный коэффициент, зависящий только от формы поперечного сечения.
Таким образом полная работа внутренних усилий для элемента длиной dx будет
dW = dWn + dWQ + dWm = [(N2 · dx) / 2EA] + [m (Q2 · dx) / 2G · A] + [(M2 · dx) / 2E · I ]
Проинтегрировав это выражение мы получим формулу полной работы внутренних усилий в пределах всего стержня
W = ò M2dx / 2E I + ò m Q2dx / 2GA + ò N2 dx / 2EA
Для стержня состоящего из N стержней результаты интегрирования можно просуммировать.
W = å ò M2dx / 2E I + å ò m Q2dx / 2GA + å ò N2 dx / 2EA (3)
Дополнительная работа внешних сил и внутренних усилий.
Приложим к балке сосредоточенную статически нарастающую силу F1.

Точкой приложения этой силы переместится по вертикали на величину D11
Вообще DIK это:
1) перемещение точки приложенной силы Fi.
2) по направлению силы Fi.
3) от действия силы Fk.
На перемещении D11 силой произведена работа F1
W11 = F1 D11 / 2
Теперь также статически в другой точки 2 приложим силу F2
При этом прогибы балки во всех точках увеличиваются, а точка 2 перемещается вниз на величину D22
W11 = F2 D22 / 2
При действии F2 силы точка 1 также переместилась вниз на величину D12
Определим работу, совершенную силой F2 на перемещении D12
W12 = F1 D12
Теорема Клайперона не применима, так как сила F1 остается постоянной на перемещении D12
W12 - дополнительная (возможная или виртуальная работа)
Определим полную работу совершенную силами F1 и F2
W = W11 + W12 + W22 = F1 D11 / 2 + F D12 + F2 D22 / 2
Из этого выражения получим величину дополнительной работы внешних сил
W12 = W - W11 - W22
Обозначим внутренние усилия возникающие в балке от силы F1 - Q1 M1 N1 , а от действия
F2 - Q2 M2 N2 . Тогда полные усилия от одновременного действия F1 и F2 будут (M1+ M2 Q1+ Q2 N1+N2)
Вычислим величины работ в соответствии с формулой (3) и подставим их в выражение дополнительной работы получим формулу дополнительной работы внутренних усилий
W12 = å ò (M1 M2)dx / E I + å ò m (Q1 Q2) dx / GA + å ò (N1 N2) dx / EA (4)
Теорема Бетти
Приложим к балке 2 статически возрастающие силы F1 и F2

Точка приложения сил F1 и F2 при этом получат перемещения.
Определяем полную работу сил W = F1 (D11 D12) / 2 + F2 (D22 D21) / 2
Но с другой стороны работа будет W = F1 D11 + F1 D12 + F2 D22 / 2
Приравняем эти выражения:
F1 (D11 D12) / 2 + F2 (D22 D21) / 2 = F1 D11 + F1 D12 + F2 D22 / 2
F1 D11 / 2+ F1 D12 / 2 + F2 D22 / 2 + F2 D21 / 2 = F1 D11 + F1 D12 + F2 D22 / 2
F2 D21 / 2 = F1 D12 - F1 D12 / 2
F2 D21 / 2 = F1 D12 / 2
F2 D21 = F1 D12
W12 = W21 (5)
Теорема: дополнительная работа сил первого состояния на перемещениях, по их направлениям вызванных силами второго состояния равна дополнительной работе сил второго состояния на перемещениях по их направлениям вызванных силами первого состояния.
Теорема Максвелла.
Приложим к балке две вертикальные единичные силы одновременно, в произвольной точки 1 приложена F1=1, а в точке 2 – F2=1. Это состояние можно рассматривать как сумму двух составляющих: 1) приложена только сила F1=1; 2) приложена только сила F2=1.
Обозначим перемещение точки 1 во втором состоянии d, а точка 2 в общем виде dik – это перемещение точки приложения Fi =1 по направлению Fi (mi) от действия Fk =1 (mk=1).
В соответствии с теоремой Бетти F1 ·d12 = F2 ·d21 так как F2 =F2 =1, то d12 =d21 и d ik =d ki

Теорема Максвелла.
Перемещение точки приложения любого единичного воздействия по направлению этого воздействия от катого единичного воздействия равно перемещению точки приложения катого единичного воздействия от итого единичного воздействия.
Интеграл Мора
Пусть на балку действует произвольная нагрузка (например, сосредоточенная сила F), это действительное (грузовое). Теперь в той же балке в точке 2 приложим только одну вертикальную силу, это состояние называется единичным.

Догрузим первое состояние заданной действительной нагрузкой. Вычислим дополнительную работу одной силы на перемещении D21
W21 = F · D21 =1 · D21 W21 = D21
Вывод: дополнительная работа одной силы на перемещение вызванной равно перемещению точки приложении одной силы от заданной нагрузки.
Точно такое же перемещение имеет точка 2 в действительном состоянии.
В соответствии с формулой (4) получим
D21 = W21 = å ò dx + å ò dx + å ò dx (6)
Зависимость (6) называется интегралом Морро. С его помощью можно определить перемещение любых точек системы.
M Q N – это внутренние усилия вызванные единичной нагрузкой в одной состоянии.
M Q N – это внутренние усилия от заданной нагрузки в действительном состоянии.
Примечание: если нужно определить линейное перемещение, то к заданной точке прикладывают одну сосредоточенную силу, а если угловое – один сосредоточенный момент.
Правило Верещагина.
Если сооружение состоит из прямоугольных элементов имеющих постоянную по длине элемента жесткость, то для определения перемещений необязательно использовать интегрирование по формуле (6).
Рассмотрим участок (элемент) длиной l для которого эпюра изгибающих моментов L – криволинейная, а в первом состоянии – прямолинейная.

требуется определить
интеграл вида
ò М · М · dx
Определим: М из треугольника АВС
ВС/ АВ = tg a => ВС = АВ tg a
М = (а + х) tg a
M dx = dv dv - площадь заштрихованной фигуры
ò М · М · dx = ò (а + х) tg a · dw = tg a ò (а + х) dw = tg a · Sy M
Sy M – статический момент относительно Y
Если известно положение центра тяжести фигуры и площадь всей фигуры, то статический момент будет Xc = Sy / A Sy M = w (a + xa)
ò М · М · dx = tg a · w (a + Xc)
yc – это ордината первой эпюры под центром тяжести грузовой эпюры
из треугольника C’B’A’ yc / (a + Xc) = tg a => yc = (a + Xc) · tg a
ò М · М · dx = yc · w (7)
Вывод: интеграл вида ò М · М · dx = yc · w произвольной площади первой эпюры (w) на ординату yc взятую из другой эпюры и расположенную под центром тяжести первой.
Формула (7) отличается от первого слагаемого интеграла Морро отсутствием жесткости EI, значит чтобы вычислить перемещение нужно формулу (7) разделить на EI.
Примечание: если одна из эпюр криволинейна, то площадь w может быть вычеслена для любой из эпюры.
Перемножаемые эпюры могут иметь форму треугольника, квадрата, трапеции, параболы и их комбинаций.
Рассмотрим основные случаи передвижения эпюр.

Эпюра М1 х эпюра М2 =
= yc · w = (1/2 a1 l1)
yc / 2/3l = a2 / l;
yc = a2 ·2l / 3l = 2/3 a2
Эпюра М1 х эпюра М3 =
= (1/2 a1 l1) b3/3
если перемножить эпюры
расположенные по разные
стороны от оси, то их про-
изведение отрицательно.
Эпюра М1 х эпюра М3 =
= - (1/2 b4 l) a1/3 =
= - (1/2 a1 l) b4/3
трапецию разбивают на два
треугольника и перемножа-
ют по правилу перемноже-
ния треугольников.
Эпюра М1 х эпюра М5 =
= (1/2 a1 l) (2a5/3 + b5/3)
Эпюра М5 х эпюра М6 =
(при перемножении трапе-
ции её можно разбивать на
треугольники использовать
правило перемножения тре-
угольников, но можно ис-
пользовать формулу трапеции)
= l/2 (2a5 a6 + 2b5 b6 + a5 b5 +a6 b6)
Эпюра М6 х эпюра М7 =
(скрученная трапеция)
=l/6 (-2a5 a7 + 2b5 b7 - a7 b5 + a5 b7)
Эпюра М6 х эпюра М7 =
= (a8 l) · (a5 b5 /2)
 Эпюры криволинейные.
Эпюры криволинейные.
Площадь параболы равно двум площадям
описанного вокруг неё прямоугольника.
Простая парабола
wМ9 = 2/3(qe2/8) l (qe3/12)
Эпюра М1 х эпюра М9 = - (qe3/12) a1/2
Если парабола сложная (эпюра 10), то её
раскладывают на простую параболу и
оставшуюся прямолинейной эпюру которую
перемножают по известным правилам.
Эпюра М1 х эпюра М10 =
= Эпюра М1 х (эпюра М10 + эпюра М10 ) =
= (qe3/12) (a1/2) + (a1 l /2) (2/3a10 + 1/3 b10)






