Сначала рассмотрим балку того же пролета, что и арка. Вычислим балочные поперечные силы и изгибающие моменты
Q1° = å y¢¢ = Va – F
M1° = å m1A = Va · x – F (x - a)
Чтобы определить внутренние усилия в сечении арки рассечем арку в этом месте, отбросим правую часть и рассмотрим равновесие левой части. К рассмотренной части арки нужно приложить заданные нагрузки и внутренние силовые факторы M, Q, N.
Вычислим внутренние силовые факторы
М -? å m1 = 0
Va · x – F (x - a) – Н · у - М = 0
М = M1° - Н · у (2)
Q -? возьмём сумму проекций на ось совпадающую с нормалью.
å V = 0 Q – Va · cos j + H · sin j + F · cos j £ 0
Q = Va · cos j - F · cos j - H · sin j
Q = (Va – F) · cos j - H · sin j Va - F = Q°
Q = Q° · cos j - H · sin j (3)
N -? å U = 0
N + H · cos j +Va · sin j - F · sin j = 0
N + H · cos j +(Va - F) · sin j = 0
W = Q° · sin j - H · cos j (4)
Лекция 10.
Плоские статически определяемые фермы.
Общие сведения
Ферма – геометрически неизменяемая стержневая система, образованная по второму варианту. Назначение фермы то же что и у балки, но ферму применяют для перекрытия значительно-больших проёмов, чем балки.
d – панель фермы
1)стержни верхнего пояса
2)стойки
3)раскосы
4)стержни нижнего пояса
5)узлы
Нагрузки прикладываются только к узлам фермы.
Определение усилий в стержнях ферм.
В стержнях ферм могут возникать только продольные усилия: растягивающие (+) или сжимающие (-). Усилия определяются после вычисления реакций опор, которые рассчитывают как для простой балки.
Два способа расчета усилий:
1. Способ равновесия дисков (сквозных сечений).
2. Способ равновесия узлов.
Способ равновесия дисков.
Это основной способ. Для его реализации форму рассекают на две части (диска), отбросим одну из частей и рассмотрим равновесие оставшегося диска. К этому диску приложены заданные нагрузки и неизвестные усилия в виде продольных сил. Направление этих сил совпадает с направлением рассеченных стержней. Достоинство этого способа состоит в возможности определения усилий независимо друг от друга.
Алгоритм №1.
Рассмотрим реализацию алгоритма на примере.
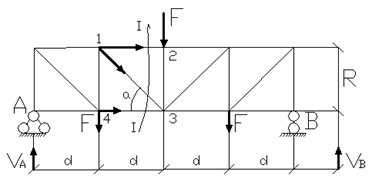
N1.2 -?
Va = å mb = 0
Vb = å ma = 0
1. Через стержень, в котором определяется усилие, провести сечение и провести его. Сечение должно быть:
а) сквозным
б) не пересекать более трех стержней.
Если нельзя провести сквозное сечение через три и более стержней, то смотрите пункт 2.
2. Для рассмотрения равновесия выбрать тот диск, к которому приложено меньше нагрузок. Выберем левый диск.
3. Показать направления усилий в рассеченных стержнях, действующих на выбранный диск. Усилия направлять к сечению.
4. Найти моментную точку (м.т.). Для нахождения м.т. нужно мысленно исключить искомое усилие и найти точку пересечения линий действия в оставшихся рассеченных стержнях. М.т. – 3. Если м.т. нет, то смотрите пункт 6.
5. Используя условие сумма моментов сил действующих на рассматриваемый диск относительно м.т. Составить и решить уравнение равновесия.
å m3 = 0
N1.2 · h + Va · 2d – F · d = 0
N1.2 = (Fd-Va2d)/h
6. Если м.т. нет, то используется условие равенства нулю суммы проекций сил действующих на рассматриваемый диск на ось перпендикулярную остальным рассеченным стержням. Составить и решить уравнения равновесия
Например найти усилие стержня 1,3
N1.3 -? м.т. – нет
å у = 0
- N1, 3 · sin a + Va –F = 0
N1.3 =
7. После определения усилий во всех рассеченных в данных сечениях, сделать проверку для которой принять одно из неиспользованных условий равновесия.
Способ равновесия узлов.
Этот способ можно рассмотреть как частный случай способа равновесия дисков.
Когда сквозное сечение пересекает только один из поясов фермы, при этом ферма распадается на диск и узел и для расчета рассмотрим равновесие узла.
Алгоритм №2
N2,.3 -?
å уВЕРХ = 0
N2,.3 + F = 0
N2,.3 = - F
Рассмотрим его на примере определения усилия в стержне 2,3.
1. через стержень, усилие в котором определяется провести сквозное сечение, отсекающее один из узлов данного стержня (выбирают тот узел, в котором сходится меньше стержней).
2. Показать направление усилий в рассеченных плоскостях, направить их от узла к сечению.
3. Провести ось перпендикулярно не вычисленным усилиям.
Примечание: если нельзя провести ось перпендикулярно не вычисленным усилиям, то ось проводят произвольно.
4. Используя условие равновесия в виде суммы проекций на выбранную ось, составить и решить уравнение равновесия.
Расчет трех шарнирной арки.
Для заданной арки определить изгибающий момент, поперечную силу, продольную силу в заданном сечении.
Определение вертикальных реакций опор.
Va -? å mв = 0
Va · 24 – 20 · 21 – 6 · 6 · 15 – 20 – 40 · 4,5 = 0
Va = 48,33 кН
Vв -? å ma = 0
Vв · 24 + 40 · 19,5 – 20 + 6 · 6 · 9 + 20 ·8 = 0
Vв = 47,67 кН
å у = 48,33 + 47,67 – 20 – 6 · 6 – 40 = 96 – 96 = 0
Определение распора
На -? å m A = 0
48,33 · 12 – Ha · 6 - 20· 9 – 6 · 6 · 3 – 20
Ha = 45,33 кН
Нв -? å m ПР = 0
Hв · 6 47,67 · 12 + 40 · 7,5 = 0
Hв = 45,33 кН
å у = На – Нв = 45,33 – 45,33 = 0
Н = (На + Нв)/ 2 = 45,33 кН
Определение балочной поперечной силы
Q1 ° = å y Л = 48,33 – 20 – 6 · 3 = 10,33
Q 2 ° = å y ПР = - (47,67 - 40) = 7,67
Определение балочного изгибающего момента
М1 ° = å m Л = 48,33 · 9 – 20 · 6 – 6 · 3 · 1,5 = 288 кНм
М2 ° = å m ПР = - (47,67 · 6 + 40 · 1,5) = 226 кНм
Определение геометрических параметров сечения
y = (4f / f 2) · x (l - x)
y1= (4 · 6/ 242) · 9 (24 - 9) = 5,625
y2= (4 · 6/ 242) · 18 (24 - 18) = 4,5
tg a = (4f / l2) · (l -2x) a - угол наклона касательной к горизонту
tg a1= (4 · 6/ 242) · (24 –2 · 9) = 0,25
tg a2= (4 · 6/ 242) · (24 –2 · 18) = - 0,5
cos a =1/ Ö(1+tg2 a)
sin a = tg a · cos a
sin a1 = 0,2425 cos a1 = 0,970
sin a2 = - 0,4472 cos a2 = 0,8944
M, Q, N – определяем в заданном сечении арки
М1 = М1 ° - H · y1 = 288 – 45,33 · 5,625 = 33,02 кН
Q1 = Q1 ° cos a1 - H sin a1 = - 10,33 · 0,97 – 45,33 · 0,2425 = - 0,97 кН
N1 = Q1 ° sin a1 - H cos a1 = - 10,33 · 0,2425 –45,33 · 0,97 = - 46,48 кН
М2 = М2 ° - H · y2 = 226 – 45,33 · 4,5 = 24,02 кН
Q2 = Q2 ° cos a2 – H sin a2 = - 7,67 · 0,2044 – 45,33 · (- 0,4472) = 13,41 кН
N2 = Q2 ° sin a2 - H cos a2 = – (- 7,67) · (- 0,4472) - 45,33 · 0,8944 = 43,97 кН
Расчет простой фермы.
Для заданной фермы требуется определить усилия в четырех стержнях заданной панели (из двух стоек выбирают правую).
Определение реакций опор
Va -? å mв = 0 Va = 82,5 кН
Vв -? å ma = 0 Vв = 82,5 кН
å у =
Усилия в стержнях
N1.2 -? сечение 1-1
м.т. 3
å m3 Л = 0
N1.2 · h 1.2 + 82,5 · 6 – 7,5 · 6 – 30 · 6 = 0
tg a = 3 / 9 = 0,33333
sin a = 0,316 cos a = 0,949
sinb =cosb = 0,7071
tg b = 3 / 3 = 1
h 1.2 = 4 cosa = 4 · 0,949 =3,8 м
N1.2 = - 94,7 кН то есть произходит сжатие
N1.3 -? h 1.3 – 82,5 · 6 + 7,5 · 6 + 30 · 9 = 0
АА¢ / 2 = ctg a = 1/ tg a = 1/ 0,3333 = 3
h 1.3 / 1.2 = sin b = 0,7071
h 1.3 = 8,48 N1.3 = 21,2 кН
N4 3 -?
МТл – 1
å m1 = 0
N1.3 · h 1.3 + 82,5 · 3 – 7,5 · 3 = 0
h 4.3 = 3
N4 3 = 75 кН
Проверка
å x ЛЕВ = N1 2 cos a + N1 3 cosb + N4 3 = -94,7 · 0,949 + 21,2 ·,7071 +75 =89,99 – 89,87 = 0,12
e = (0,12 / 89,99) · 100% =0,13 % e £ 1%
МТ – A’
å mA’ ЛЕВ = 0
-N2.3 · h 2.3 - 82,5 · 6 + 7,5 · 6 + 30 · 9 + 30 · 12 = 0
N2.3 = - 15 кН
Лекция 11.
