ГЛАВА 5
Изгиб.
Внутренние усилия.
При действии на брус нагрузок расположенных в плоскости прох. через ось бруса в поперечных сечениях бруса возникают следующие внутренние силовые факторы:
1. Продольная сила N приложенна к центру тяжести сечения и направленых вдоль оси.
2. Поперечная сила Q действующая в плоскости поперечного сечения.
3. Изгибающий момент М действующий в плоскости перпендикулярно поперечному сечению.

| N>0,если направленно от сечения Q>0,если стремится вращать рассмотренную часть бруса по часовой стрелке М>0,если действует на левую часть против часовой стрелки, а на правую по часовой стрелке. Или говорят, М>0, если растягивает нижние волокна бруса |
Связь между внутренними силовыми функциями имеет вид
М = 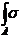 ydA; Q =
ydA; Q =  dA; N =
dA; N =  dA (1)
dA (1)
Установим связь между внутренними силовыми факторами внешними нагрузками.
Величина изгибающего момента равна сумме моментов всех внешних сил приложенных к левой части бруса, или сумме правых сил, но с обратным знаком.


(2)
M > 0,если сила стремиться вращать по часовой стрелке.
Величина поперечной силы Q равна сумме проекций всех внешних сил приложенных к левой части бруса на нормаль к его продольной оси или сумма проекций взятой с обратным знаком всех внешних сил приложенных к правой части бруса.
(3)
Проекция больше нуля, если направлена вверх. Итак,моменты и проекции сил определяют от внешних нагрузок расположенных по одну сторону от рассматриваемого сечения. По величинам моментов в характерных точках бруса можно построить график изменения моментов по длине бруса, который называется эпюрой изгибающих моментов М. Аналогичной эпюрой поперечных сил Q называется график изменения поперечной силы по длине бруса.
Опоры балок.
Балка – это брус, работающий на изгиб.
Опора – это устройство, обеспечивающее связь балки с основанием.
Под действием внешних нагрузок в опоре возникают силы, которые называются реакциями опоры.
Реакции могут быть 3 видов:
1. Вертикальная сосредоточенная сила V.
2. Горизонтальная сосредоточенная сила H.
3. Реактивный момент М.
Вид и количество реакций зависит от конструкций опоры.
Величины опорных реакций определяются с помощью уравнений статики.
Дифференциальные зависимости между М, Q, и интенсивностью распределенной нагрузки q.
Пусть дана балка загруженная произвольной нагрузкой находящейся в вертикальной плоскости.
Расположим начало координат на левой опоре.

На расстоянии х от левой опоры вырежем из балки элемент dx и рассмотрим его равновесие. Т. к. вся балка находится в равновесии, то и ее элемент dx также будет в равновесии.
А это значит, что нагрузки приложенные к нему должны удовлетворять условию равновесия.



Равнодействующая распределенной нагрузке равно площади эпюры.


Слагаемые  отбросим как величину бесконечно малую второго порядка малости,тогда
отбросим как величину бесконечно малую второго порядка малости,тогда
 (4)
(4)
Вывод: Первая производная от поперечной силы по х равна сумме интенсивного распределения
нагрузки q.
 ;
; 


Первая производная изгибающего момента по абсциссе равно поперечной силе. Эта зависимость называется теоремой Журовского. так как первая производная равна тангенсу угла наклона касательной к оси х, то Q = tg M, где угол между касательной к эпюре М и осью х. -Если эпюра М в виде прямой линии, то tg M = const и эпюра Q прямая параллельная х. –Если эпюра М в виде прямой линии, то tg M = const и изгибающий момент будет экстремальным, там где Q = 0.
Эпюры внутренних усилий.
Эпюры будем строить разбив балку на участки.
1. Приложение сосредоточенных сил.
2. Начало, конец участка q и точек между ними.
3. Приложение сосредоточенных элементов (для эпюры М)
4. Опоры.
Случай 1.Простая балка загруженная сосредоточенными силами.

|   

  
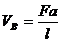 Проверка:
Проверка: 

|
Нанесем на схему и определим реакции опор.
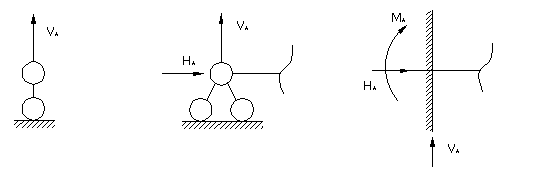
Разобьем балку на участки границами которых являются точки а, с, в и вычислим величины поперечных сил и изгибающих моментов в пределах этих участков. Их значения на границах участков поместим в таблицу.
Начало координат расположим в точке а и ось х на правим в право.
| А | Сл | Спр | В | |
| Q, кН | Fb l | Fb l | Fa l | Fa l |
| М, кН м | 0 | Fab l | Fab l |
Участок АС: 




Участок СВ: 



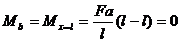
По вычисленным ординатам отложенных от нулевых линий построим эпюру.
Положение ординат эпюры Q откланяется вверх от нулевой линии, эпюра М отклоняется вниз. Ординаты должны быть в масштабе, который различен для эпюр Q и М. От сосредоточенной силы на эпюре Q должен быть скачек равный величине силы. Направление скачка совпадает с направлением силы при движении эпюре с лева на право.
Случай 2.Балка загружена сосредоточенным моментом.

|  ; ;  ; ;  ; ;  ; ;
 ; ;  ; ;  ; ;  ;Проверка: ;Проверка:  Участок АС:
Участок АС: 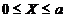
 ; ;  ; ;  ; ;  ;
Участок СВ: ;
Участок СВ:  



|
| Случай 3 Балка загружена распределенной нагрузкой. | |

|  ; ;  ; ;  ; ;
 ; Проверка: ; Проверка:
 ; ;
 ; ;
 ; ;
 ; ;
 ; ;
 ; ;

|
Случай 4. Консоль загруженная сосредоточенной силой.
Начало координат расположим в торце консоли в точке В, а ось х направим влево.

| 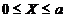 ; а - вылет консоли ; а - вылет консоли


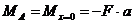
|
Вывод: В конце консоли всегда «0» за исключением случая приложения сосредоточенного момента.
Случай 5 Консоль загруженная сосредоточенным моментом.

| 





|
Напряжения при изгибе.
При изгибе поперечные сечения плоские до деформации остаются плоскими и в процессе изгиба.
Рассмотрим консоль загруженную сосредоточенным моментом.
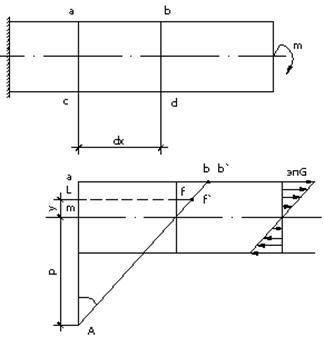
| Во всех поперечных сечениях изгибающие моменты одинаковы и равны м. Это состояние чистого изгиба. Проведем два поперечных сечения отстоящих друг от друга на расстоянии dx. При изгибе эти сечения повернутся относительно друг от друга на угол dU.Примем условно левое сечение за неподвижное, тогда в результате поворота правого сечения на угол dU она займет положение . При этом волокно ab растянется, а cd сожмется. Точка А – центр кривизны mn - нейтральный слой (не меняет свою длину при изгибе).На растоянии y от оси mn выделим волокно lf и рассмотрим его деф в процессе изгиба. |
Точка f – перейдет в f, тогда 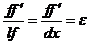 - относительное удлинение
- относительное удлинение
Рассмотрим треугольник nff и подобный треугольник Amn.
Из  , т.к.
, т.к.  , то
, то  (6)
(6)
Все продольные волокна при чистом изгибе растянуты или сжаты, а косательные напряжения равны нулю. По закону Гука нормольное напряжение  или с учетом (6)
или с учетом (6)
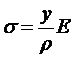 (7)
(7)
Нормальное напряжение прямопропорционально расстоянию от рассматриваемого волокна до оси mn. по одну сторону от оси будет растяение, а по другую – сжатие.
Эпюра  - это график определяемый прямой линией. При чистом изгибе продольная сила во всех сечениях равна нулю.
- это график определяемый прямой линией. При чистом изгибе продольная сила во всех сечениях равна нулю.

(8)
Подставим в интеграл выражение (7),получим
 ;
;  ;
;  - статический момент отн. Z, т.к.
- статический момент отн. Z, т.к.  ,
,
то остается 
Статический момент равен нулю относительно центральной оси.
Вывод: нейтральная ось z перпендикулярная mn проходящая через центр тяжести поперечного сечения. известно, что изгибающий момент относительно оси z
 ;
; 
Тогда в соответствии (7) получим

 (9)
(9)
При чистом изгибе балки постоянного сечения величины Мz, Iz являются величинами постоянными, отсюда следует, что p так же постоянна т. е. Изогнутая ось представляет собой окружность.Максимальное нормальное напряжение в соответствии с (9) в данном сечении будет:

Введем обозначение  - осевой момент сопротивления.Отсюда формула
- осевой момент сопротивления.Отсюда формула

 Например для прямоугольного сечения
Например для прямоугольного сечения
 ;
; 
При поперечном изгибе в поперечном сечении балки возникают изгибающий момент и поперечная сила. Поперечная сила Q связанна с косательными напряжениями зависимостью 
Косательные напряжения определяются по формуле Журавского 
Рассмотрим сечение и момент инерции всего сечения относительно нейтральной оси и b – ширина поперечного сечения. Направление определяется касательным напряжением для прямоугольника на расстоянии y от нейтральной оси

| 

|






